260
Proceedings of the 18
th
International Conference on Soil Mechanics and Geotechnical Engineering, Paris 2013
Proceedings of the 18
th
International Conference on Soil Mechanics and Geotechnical Engineering, Paris 2013
Un domaine élastique
situé à l’intérieur de l’ellipse
dont l’axe principal est la droite déduite de k
0
=
’
3
/
’
1
.
Le point I qui fixe sa longueur est obtenu à partir de la
pression de consolidation
’
p
.
Cette ellipse, appelée SEL,
représente la projection de la Surface d’Etat Limite dans
ce plan. A l’intérieur de l’ellipse les déformations sont
élastiques réversibles. Cette ellipse projetée dans un plan
perpendiculaire au plan de représentation de l’œdomètre
[e, log
] s’appuie sur la droite C
s
. Les points d’état ne
peuvent franchir la SEL.
Un domaine plastique.
Lorsque le point représentatif
de l’état de contraintes considéré atteint la surface de
rupture, caractérisée par les droites limites de Mohr-
Coulomb (SEC
,
Surface d’Etat Critique), il y a rupture du
sol avec des phénomènes de radoucissement.
Étude du déchargement à l’aide du modèle Ylight
Dans la phase de déchargement généralisé (érosion), les
déformations horizontales sont nulles :
.
0
3
En fin de chaque phase de déchargement, une fois
l’équilibre atteint, les pressions interstitielles sont
supposées constantes et en équilibre avec celle du niveau
considéré.
Dans le
domaine
élastique
Dans ce domaine, il est possible d’écrire :
1
1
3
(1)
où représente le coefficient de Poisson
.
Il vient alors :
et
1
e
γh
1
3
e
h
(2)
Dans le plan
[s’,t]
, cela se traduit par :
) 1(2
1
'
e
h s
et
) 1(2
21
e
h t
(3)
La pente de la droite représentant le déchargement
élastique du sol est p =1-2v
.
Au point I l’état de
contrainte s’écrit :
2
)
1( '
'
0
k
s
P
et
2
)
1( '
0
k
t
P
(4)
En tenant compte des équations (2), (3) et (4), l’équation
de la droite de déchargement dans l’espace
est :
ts
,'
0 0
)
1( '
')21(
k k
s
t
P
(5)
Celle-ci intercepte la SEL au point C. A partir de ce
point d’équilibre correspondant à la contrainte
verticale
’
v0
qui à une profondeur donnée est
constante (
’
v0
=
.z), le déchargement par excavation
(déblai) s’effectue suivant un chemin de contraintes (s’, t)
correspondant à une droite de pente –1, qui coupe la
courbe d’état critique au point G.
Dans le domaine
plastique
Lorsque le déchargement se poursuit le chemin de
contrainte suivi passe sur la droite GO.
/
Le point G représente le passage entre le comportement
élastique caractérisé par
l’indice
de gonflement C
s
et le
comportement plastique caractérisé par le coefficient de
gonflement C
g
.
3. ANALYSE DES PHENOMÈNES
DE GONFLEMENT A L’OEDOMÈTRE
3.1. Essai de gonflement (norme XP P94-091)
Cet essai à l’oedomètre consiste à mesurer, sur quatre
échantillons prélevés à la même profondeur, les
gonflements obtenus lors de la saturation sous quatre
contraintes différentes, la contrainte de gonflement
donnant un gonflement nul.
En fait, cette contrainte devrait correspondre à la
contrainte effective verticale obtenue à la profondeur
(profondeur de prélèvement des échantillons) :
.
z
z
v
,
0
Dans ces conditions l’exploitation des mesures consiste
à reporter sur un diagramme logarithmique les valeurs
finales des différentes déformations mesurées en fonction
du rapport
g
dans l’espace
log ,
i
f
H
H
. Ces différents
points s’alignent sur une droite, dont la valeur absolue de
la pente est appelée rapport de gonflement :
.
R
g
Nous avons la relation :
H
f
/H
i
R
g
log(
g
/
)
(6)
g
étant la contrainte qui correspond à une déformation
nulle, soit la contrainte effective correspondant au poids
des terres.
3.2. Essai oedométrique classique adapté
La norme XP P94-090-1 a été adaptée pour la
circonstance afin de détailler le gonflement des sols
surconsolidés au déchargement.
La courbe de déchargement mesurée dans un œdomètre à
partir de la pression de consolidation maximale est obtenue
en déchargeant par paliers successifs l’échantillon imbibé à
partir de cette pression. Elle fait apparaître typiquement
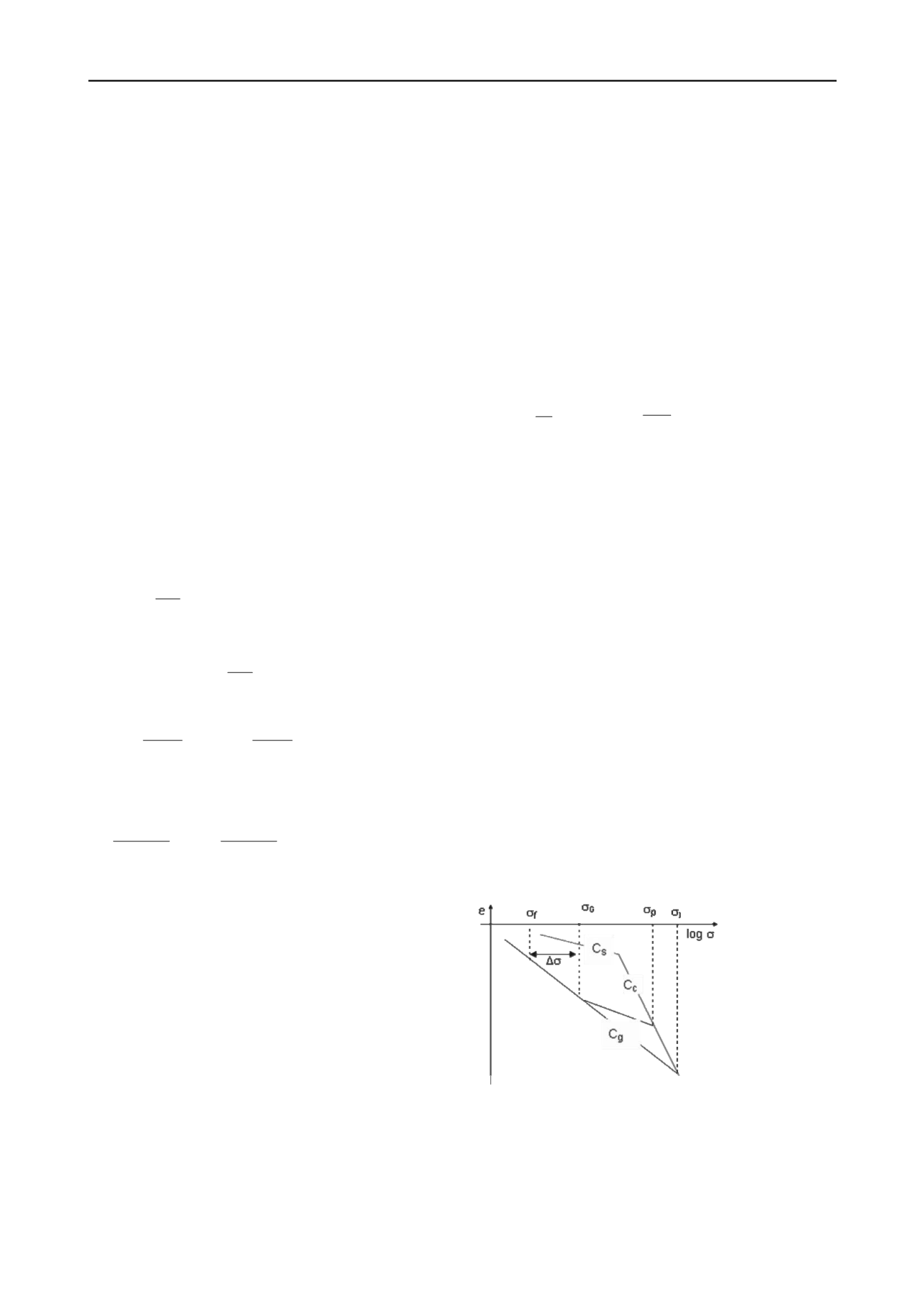
deux branches de droites (figure 2) :
La première
, de pente dans la représentation
œdométrique
C
s
log ,
e
;
La seconde
, de pente donnée par l’équation (6)
,
que nous
noterons
,
étant l’indice des vides
avant déchargement.
) 1/(
i
g
g
e
R C
i
e
Ces deux droites se coupent en un point qui correspond à
la contrainte notée
G
, pour
la distinguer de la contrainte
Gg
définie ci-dessus.
Figure 2. Courbe de déchargement à l’œdomètre
3.3. Elaboration d’un modèle de calcul
Le modèle Ylight nous a permis de montrer que la
contrainte
G
correspondait à la transition entre le
comportement élastique du sol et le comportement
irréversible de caractéristiques respectives C
s
et C
g
.
2


