Actes du colloque

2737

Technical Committee 212 /

Comité technique 212

Thus, with sample growth, the standard deviation increases,

and the probability density around the mean decreases, leaving

the curve with a flatter appearance (recalling that the area

considered between the standard curve and the abscissa is equal

to the unity) . This can be seen in Figure 3, which depicts the

variation of the shape of the standard curve, due to the growth

of the sample until the final number of load tests performed (N

= 27).

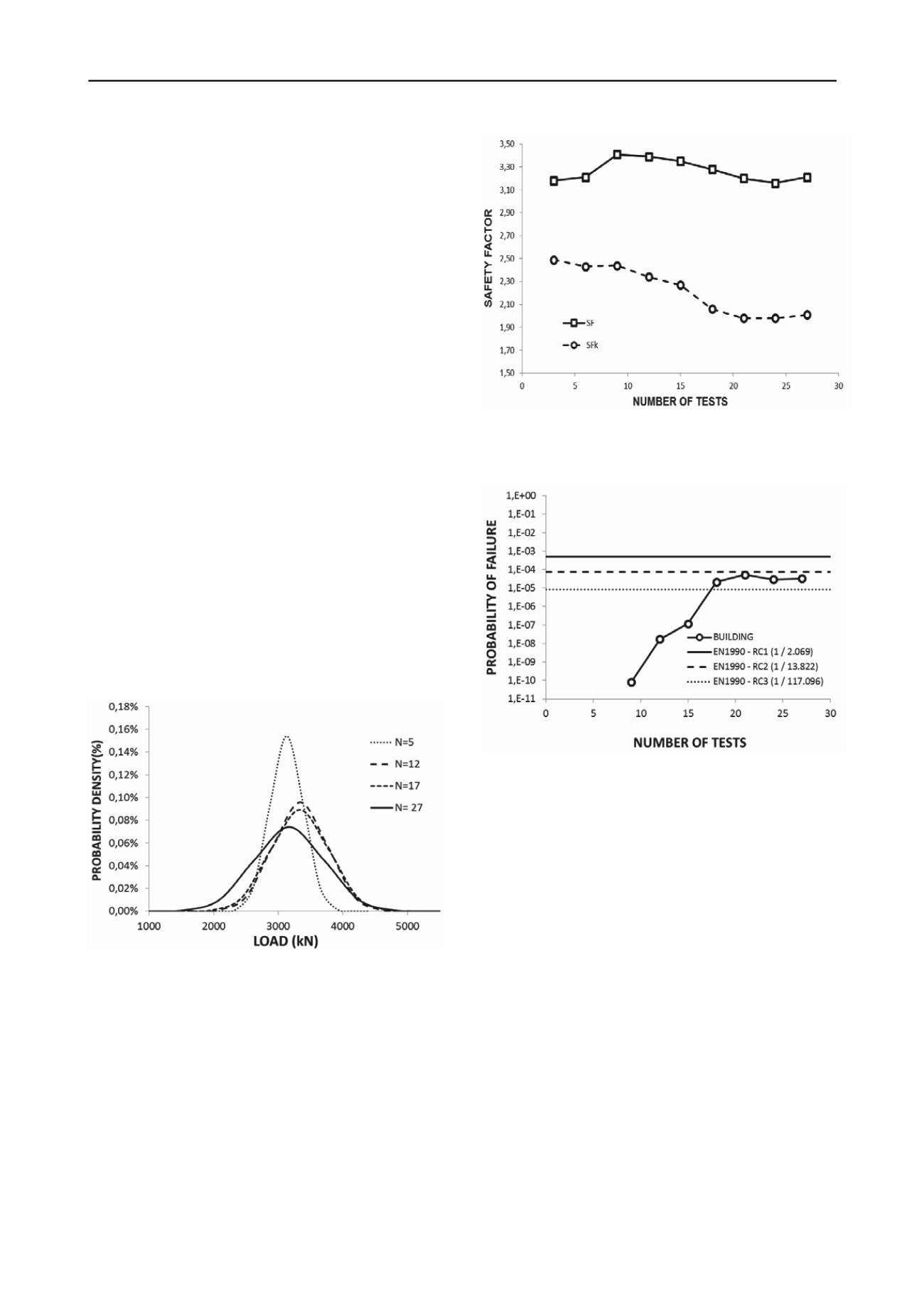
In a deterministic analysis, foundation safety is verified by

means of the Global Safety Factor (FSg), which is the ratio

between the mean resistance and mean requirement. However,

for an analysis where the effects of sample dispersion are

intended to be considered, as with Probability of Failure, the

Safety Characteristic Factor (FSk) must be also considered. This

factor is defined as the ratio between the Resistance

Characteristic (Rk) and the Requirement Characteristic (Sk).

The Resistance characteristic represents the mean resistance

increased from Z.σR, as well as the characteristic that is

obtained by minimizing the mean requirement in Z. σS (where

Z represents the reliability interval, usually equal to 95%,

equivalent to Z = 1.65). Figure 3b makes comparison between

the Global Safety Factor, and the Safety Characteristic Factor as

the sample increases.

Figure 4. Variation of global and partial safety factors relative to the

number of load tests

.

As already seen, as sample space increases, population

dispersion is incorporated into the sample, and the standard

deviation tends to increase. In this manner, as dispersion

increases, the reliability index represented by β decreases and

eventually the Probability of Failure increases. Thus, on the

basis of everything that has been presented, it was verified that

with an increase in number of load tests, the probability of

failure increased until practically constant between the values of

15 and 20 load tests performed, i.e. 0.35 to 0.48% of the project

piles tested. Figure 5 shows the variation of failure probability

in function of the increase of the number of load tests, compared

with the limits set by the European code EN1990.

Figure 5. Variation of the probability of failure with an increase in the

number of load tests.

3 CONCLUSIONS

With growth of the sample, the standard deviation increases,

and probability density around the mean decreases, leaving the

curve with a flatter appearance. As sample space increases,

population dispersion is incorporated into the sample, and the

standard deviation tends to increase. As the dispersion

increases, the reliability index represented by β decreases, and

probability of failure increases. It was possible to verify that

with an increase in the number of load tests, the probability of

failure increased until practically constant when reaching 15 and

20 load tests performed, and 0.35 to 0.48% of the project piles

having been tested. The safety characteristic factor showed to

be, as expected, always less than the global security factor,

however, with values remaining above levels permitted by

codes.

Figure 3. Standard curves varying according to the number of

load tests analyzed.

4 REFERENCES

Gusmão Filho, J.A; Gusmão, A.D. and Maia. G.B. 1998. Prática de

fundações na cidade do Recife: Exemplos de Casos (in Portuguese). 12º

Congresso Brasileiro de Mecânica dos Solos e Engenharia Geotécnica,

Brasília, Vol.3, pp.1415-1422.

Thus, with sample growth, the standard deviation increases,

and the probability density around the mean decreases, leaving

the curve with a flatter appearance (recalling that the area

considered between th standard curve and the abscissa is equal

to the unity) . This can be seen in Figure 3, which depicts the

variation of the shape of the standard curve, due to the growth

of the sample until the fin l number of load tests performed (N

= 27).

In a deterministic analysis, foun ation safety is verified by

means of the Global Safety Factor (FSg), which is the ratio

between the mean resistance and mean requirement. However,

for an analysis where the effects of sample dispersion are

int nded to be considered, as with Probability of Failure, the

Safety Characteristic Factor (FSk) ust be also considered. This

factor is defined as t e ratio between the Resistance

Characteristic (Rk) and the Requirement Characteristic (Sk).

The Resistan e characteristic represents the mean resistance

increased from Z.σR, as well as th characteristic that is

obtained by minimizing the mean requirement in Z. σS (where

Z represents the reliability interval, usually equal to 95%,

equiv lent to Z = 1.65). Figur 3b mak s comparison between

the Global Safety Factor, and the Safety Characteristic Factor as

the sampl increases.

Figure 4. Variation of global and partial safety factors relative to the

number of load tests

.

As already seen, as sample space increases, population

dispersion is incorporated into the sample, and the standard

deviation te ds to increase. In this manner, as dispersion

increases, the reliability index represented by β decreases and

eventually the Pr bability of Failure increases. Thus, on the

basis of everything that has been presented, it was verified that

with n incr as in number of load tests, the probability of

failure increas d until practically constant betw en the values of