2543
Technical Committee 211 /
Comité technique 211
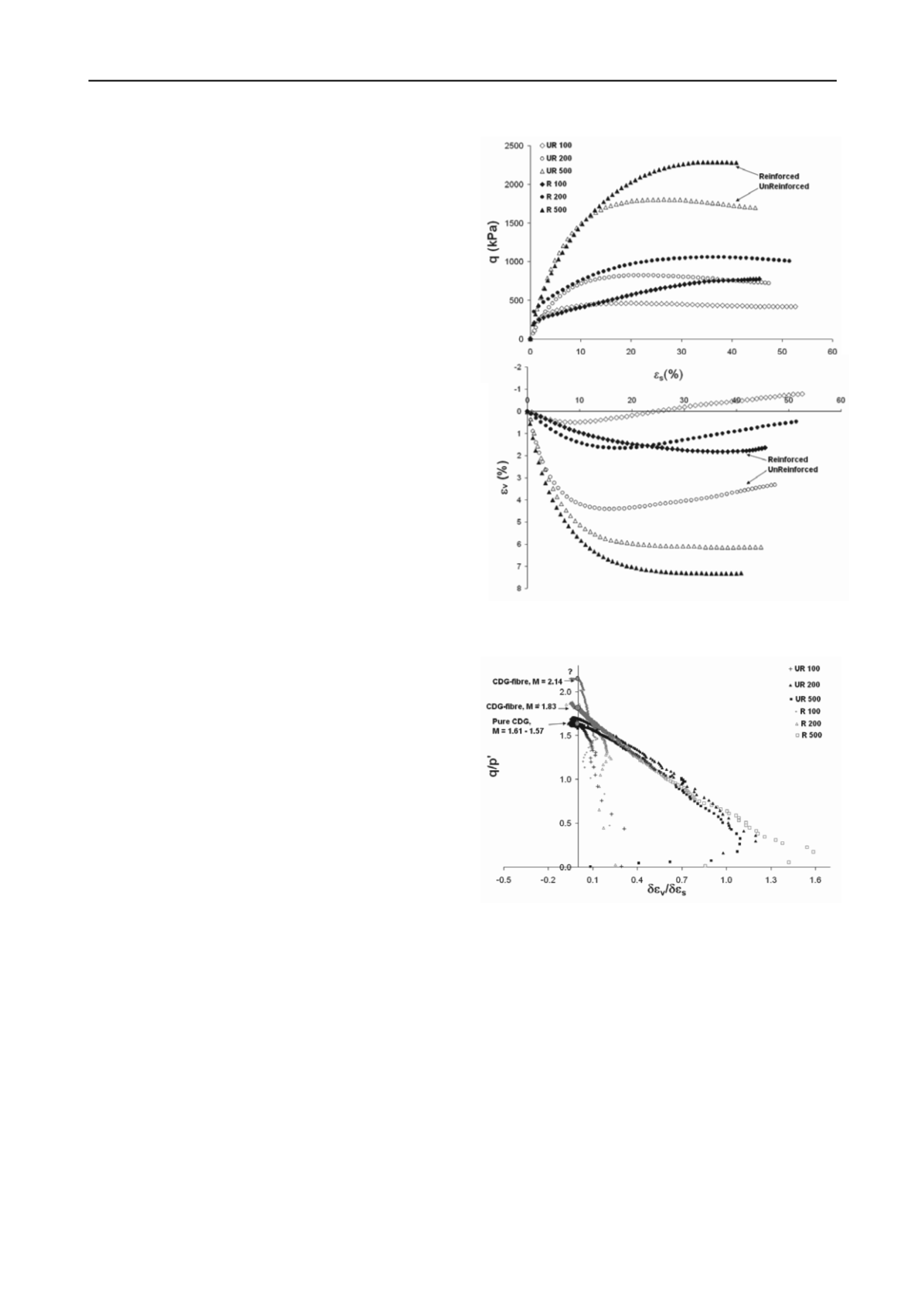
strength and higher initial stiffness at the beginning of shearing,
when compared to their unreinforced counterparts. However the
reinforced specimens that mobilised their full strength only did
so at shear strains in excess of 20%. The unreinforced
specimens on the other hand either reached a constant stress by
20% strain or they showed strain-softening, depending on their
consolidation history. Unlike the other reinforced specimens,
R100 kept gaining strength and never reached critical state even
at large strains (about 50%). This may be due to the over-
consolidation history of the specimen, which may have released
some of the tension in the fibres prior to shearing. The peak
strengths of reinforced CDG were calculated to be 1.76
(100kPa), 1.29 (200kPa) and 1.26 (500kPa) times that of the
pure CDG.
Similar behaviour on fibre-reinforced sands is reported by
Consoli
et al.
, 2007, Consoli
et. al
(2005) and Silva dos Santos
et al
. (2010). For example Silva dos Santos
et al
. (2010) found
that the effect of fibres depends on the effective stress at which
they are sheared, reducing marginally with increasing effective
stress. For sands, it is already reported that at low effective
stress, adding fibres contributes to reducing the degree of
dilation in the reinforced specimens (Silva dos Santos
et al
.,
2010). The persistent strain hardening behaviour (figure 3a,
R100) was also observed by Consoli
et. al
(2005) on Botucatu
residual soil, however their data were limited to strains of about
25%. In the present study, the specimens were sheared to strains
up to 50% and it is clear that the strain hardening behaviour of
specimens R200 and R500 stopped beyond
s
>35% to reach a
critical state. The governing mechanism for the strain hardening
behaviour of R100 specimen might therefore be due either to
the effect of low effective stress or to the effect of over-
consolidation, or a combined effect.
The effect of the fibres on the volumetric response of the
reinforced CDG in comparison seems to be that of restricting
the degree of dilation in the specimen sheared at lower effective
stresses, while at higher effective stress this effect is not so
evident (figure 3b). The over-consolidated specimen of
reinforced CDG shows a different volumetric response i.e. it
tends to dilate after 20% shear strain even though it is expected
that reinforcement will impede dilation. This behaviour is again
either due to over-consolidation or to low effective confining
stress. Previous findings on Botucatu residual soils (Consoli
et.
al,
2005) and other pure sands may be extrapolated to normally
consolidated CDG, but the effect of over-consolidation is new
and more test results are required to explain it within the critical
state framework.
The stress-dilatancy behaviour of CDG (black symbols) and
reinforced CDG (grey symbols) samples tested at different
effective stress are shown in figure 4. All normally consolidated
specimens, reinforced and unreinforced, show a typical
frictional behaviour. The pure CDG specimens converge to a
unique critical state stress ratio ranging from
M
=1.57 to
M
=1.61. The reinforced CDG specimens tested at effective
stresses of 200 and 500kPa converged to a critical stress ratio of
M
= 1.83. For the lower effective stress of 100kPa (R100), the
specimen reached a higher stress ratio of
M
= 2.14, which is
similar to what was found by Silva dos Santos
et al
. (2010) on
fibre-reinforced sand. The over-consolidated specimens, UR100
and R100, did not follow the frictional trend but showed much
less volumetric deformation up to critical state, which was also
observed in the stress-strain behaviour. This may have been
caused by locking of the fibres during compression and swelling
prior to shearing.
(a)
(b)
Figure 3. Stress-strain-volumetric response of CDG and fibre-
reinforced CDG sheared at different effective confining stresses.
Figure 4. Stress-dilatancy response of CDG and fibre-reinforced
CDG.
The deviatoric stress and corresponding mean effective
stress in the test that reached a stable critical state are plotted in
a q-p
'
plane in figure 5. These points form a critical state
envelope for the pure CDG with a critical state gradient
M
=1.57. This is found to be consistent with critical stress ratio
M
= 1.57 - 1.61, obtained from the stress-dilatancy plot (figure
4). The end of test points are also plotted for the reinforced
specimens but no attempt has been made in this paper to define
the critical state envelop for fibre-reinforced CDG because at
low stresses, the deviatoric stress does not stabilise (figure 3a).
More tests are required over a larger range of stresses to do so,
as was done by Silva dos Santos
et al
. (2010) who found that
the critical state lines of the unreinforced and reinforced
specimens converge at large stresses of the order of 5MPa.


