2389
Technical Committee 209 /
Comité technique 209
2...
1 N=0
Q
max
k
l
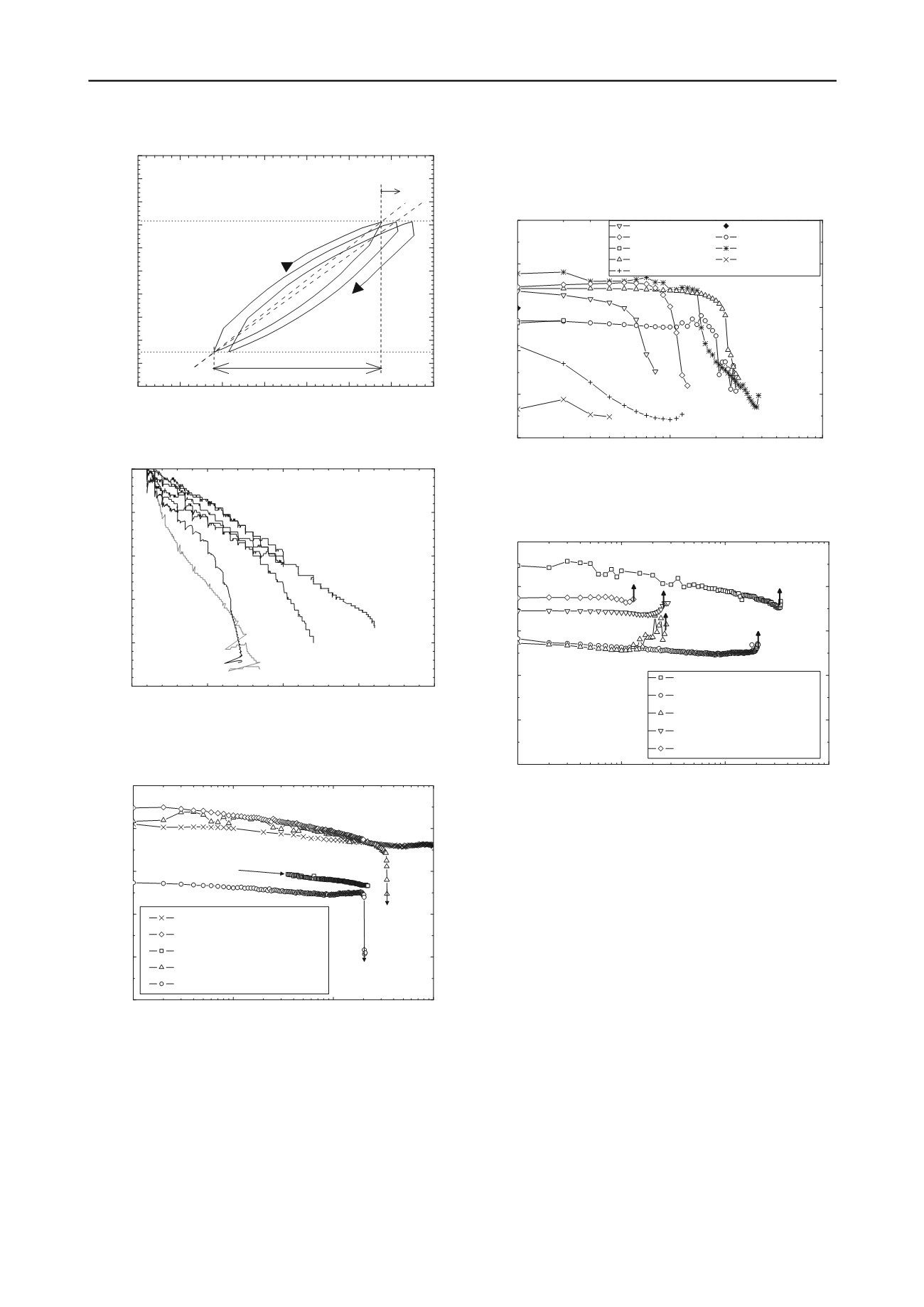
a: Permanent accumulated cyclic displacement
k l : Loading cyclic stiffness
k u : Unloading cyclic stiffness
k
u
Pile head load, Q (kN)
transient displacement, d
a
Displacement, s (mm)
Q
min
Figure 4. Illustration of the stiffness and displacement parameters used
in the analyses
0
5
10
15
20
0.0
0.2
0.4
0.6
0.8
1.0
R1
C1
k l /k Ref
Q/Q Ref
R2 - R6
Figure 5. Pile stiffness from the first–time axial static monotonic tension
loadings normalised by the reference stiffnesses against normalised load
1
10
100
1000
0.0
0.2
0.4
0.6
0.8
1.0
Q cyc = 0.3Q T
Q cyc = 0.34Q T
All other Meta-stable tests
Stable test
k
l
/k
Ref
Cycles, N
S 3.R4.CY6; Q cyc = 0.2Q T
MS 2.R3.CY2; Q cyc = 0.3Q T
MS 2.R4.CY2; Q cyc = 0.34Q T
MS 2.R5.CY2; Q cyc = 0.3Q T
MS 3.R6.CY6; Q cyc = 0.42Q T
Data not logged for
the first 34 cycles
Q cyc = 0.42Q T
Figure 6. Axial cyclic loading stiffness k
l
responses normalised by k
Ref
against number of cycles for the stable and meta–stable tests.
The loading stiffness k
l
degradation trends for the unstable
tests (Set 3 of Figure 1) are shown on Figure 7. By definition,
these tests failed with sudden stiffness loss after relatively few
cycles. However, even these piles retained most of their initial
stiffnesses until within ~10 cycles of final failure. Seemingly
anomalous stiffness behaviour is observed towards failure in
some one–way meta-stable and unstable loading tests when
stiffnesses are defined from the unloading cycle phase k
u
,
Figure 8. This reversal in normalised stiffness results from an
increased opening-up of the load-unload hysteresis loops as
cyclic failure approaches with more plastic displacements
accumulating on the loading loops leading to the progressively
decreasing secant loading stiffnesses and apparently stiffer
behaviour on unloading as cyclic loading approaches failure.
1
10
100
0.0
0.2
0.4
0.6
0.8
1.0
k
l
/k
Ref
Cycles, N
US 3.R2.CY2 (0.40)
US 2.R6.CY2 (0.36)
US 2.R3.CY3 (0.46)
US 2.R6.CY4 (0.36)
US 2.R4.CY4 (0.44)
US 2.C1.CY3 (0.74)
US 2.R5.CY3 (0.35)
US 2.C1.CY4 (0.72)
US 2.C1.CY5 (0.66)
All Unstable tests
Figure 7. Axial cyclic loading stiffness k
l
responses normalised by k
Ref
against number of cycles for the unstable tests.
1
10
100
1000
0.0
0.2
0.4
0.6
0.8
1.0
k u /k Ref
Cycles, N
MS 2.R5.CY2 Q
cyc
= 0.30Q
T
MS 3.R6.CY6 Q
cyc
= 0.42Q
T
US 2.R6.CY4 Q
cyc
= 0.44Q
T
US 2.R5.CY3 Q
cyc
= 0.35Q
T
US 2.R3.CY3 Q
cyc
= 0.35Q
T
Figure 8. Axial cyclic unloading stiffness k
u
responses normalised by
k
Ref
against number of cycles for selected metastable and unstable tests.
4.3 Accumulated cyclic displacements
The patterns of pile head displacement accumulation for the
stable and meta–stable cyclic tests are shown on Figure 9. Also
shown are the reference lines related to the predefined
thresholds for stable, metastable and unstable accumulated
displacements rates. An almost static accumulated displacement
trend was observed in the single fully stable loading test
3.R4.CY6. The meta–stable tests 2.R3.CY2 and 2.R4.CY2
developed higher, but steady displacement rates >
1mm/100cycles while the other two meta–stable tests 2.R5.CY2
and 3.R6.CY6 displaced by > 1mm/10cycles. A range of
responses is evident for the unstable loading tests summarised
in Figure 10 which develop displacement rates > 1mm/10cycles.
While the cyclic stiffness patterns varied principally as a
function of the applied cyclic amplitudes Q
cyclic
, the
accumulated cyclic displacement patterns depended on both the
normalised mean (Q
mean
/Q
T
) and cyclic (Q
cyclic
/Q
T
) loads.
Rimoy et al. (2013) demonstrate the interactive effects of the
loading components Q
cyclic
and Q
mean
by considering the
accumulated displacements developed after 3, 10, 30, 100, 200,
and 300 cycles to produce tentative 3D surfaces equivalent to
displacements of 2%, 0.2% or 0.02% pile diameter, Figure 11.
The accumulated displacement trends flatten progressively as N
increases. The zero cyclic effect boundary was set at Q
cyclic
/Q
T
=


