2380
Proceedings of the 18
th
International Conference on Soil Mechanics and Geotechnical Engineering, Paris 2013
verticale appliquée sur la surface du massif de 150 kPa,
correspondant à une résistance de pointe pénétrométrique q
c
de
20 à 23 MPa.
Le pieu modèle instrumenté a été développé par ICL et est
décrit en détail dans Jardine et al (2009). C’est un pieu à base
fermée de 36 mm de diamètre, instrumenté en 3 niveaux le long
du fût pour mesurer les contraintes tangentielles et radiales dans
la surface du pieu. Chaque niveau d’instrumentation inclut aussi
un capteur de force. Pour les derniers essais réalisés, il a été
équipé d’un capteur de force en pointe.
L’installation initiale du pieu a été effectuée jusqu’à une
profondeur d’environ 1 m par des cycles d’enfoncement
successifs de 5 à 20 mm à une vitesse de 0,2 mm/s, suivis d’une
décharge complète, de façon à simuler les effets d’un processus
de battage.
Le programme expérimental a inclus quatorze essais
cycliques autant sous contrôle de déplacement que sous contrôle
en charge pour des cycles alternés et non-alternés (seulement en
traction).
Une première partie des résultats concernant les essais de
chargement cyclique a été présentée par Tsuha et al. (2012). On
trouvera de plus amples informations dans Rimoy et al., 2013
2.3
Critères de rupture
L’application de cycles sur un pieu installé dans du sable
provoque une succession de petits glissements relatifs sol-pieu
dont le cumul détermine le déplacement global. La vitesse de
déplacement initiale est fonction de l’amplitude Q
c
et du niveau
de chargement maximal Q
max
mais ces mêmes paramètres
conditionnent également l’évolution du frottement qui peut se
détériorer pour des cycles de grande amplitude ou s’améliorer
pour des cycles de faible amplitude (Tsuha et al., 2012). Sur un
pieu sollicité en traction, la vitesse initiale se modifie pour :
- soit conduire vers la rupture : dans ce cas la vitesse
s’accroît. La rupture peut être définie de manière
conventionnelle (par exemple pour un déplacement de la
tête du pieu de 0,1D) ou lorsque se produit une accélération
brutale du taux de déplacement ;
- soit conduire vers la stabilisation : la vitesse décroît
continument jusqu’ à passer en dessous d’un seuil où on
peut considérer que les déplacements cumulés deviennent
non significatifs.
2.4
Diagrammes de stabilité cyclique
La caractérisation complète d’un essai de chargement cyclique
suppose la définition des paramètres suivants :
Q
m
: valeur moyenne de la charge sous chargement cyclique,
Q
c
: demi-amplitude du chargement cyclique,
N
f
: nombre de cycles conduisant à la rupture,
N : nombre de cycles appliqués en l’absence de rupture,
f : fréquence des cycles (en général 0,5Hz)
L’essai est dit répété (one-way) si Q
c
< Q
m
et alterné (two-way)
si Q
c
>Q
m
. On définit de plus :
Q
u
: capacité statique ultime selon le mode considéré (Q
ut
en
traction et Q
uc
en compression).
Il est pratique de présenter les résultats d’essais de
chargements cycliques dans un diagramme où chaque série de
chargement est identifiée par le couple de paramètres
normalisés Q
m
/Q
u
et Q
c
/Q
u
. Ce type de représentation permet de
bien visualiser les zones de fonctionnement sous chargements
répétés et sous chargements alternés. Si on affecte chaque point
du nombre de cycles N
f
ayant provoqué la rupture ou du nombre
de cycles N appliqué sans provoquer la rupture on peut définir
des zones de « stabilité » ou d’« instabilité » du pieu. On voit
que la taille de ces zones dépend du (des) critère(s) de rupture
choisis.
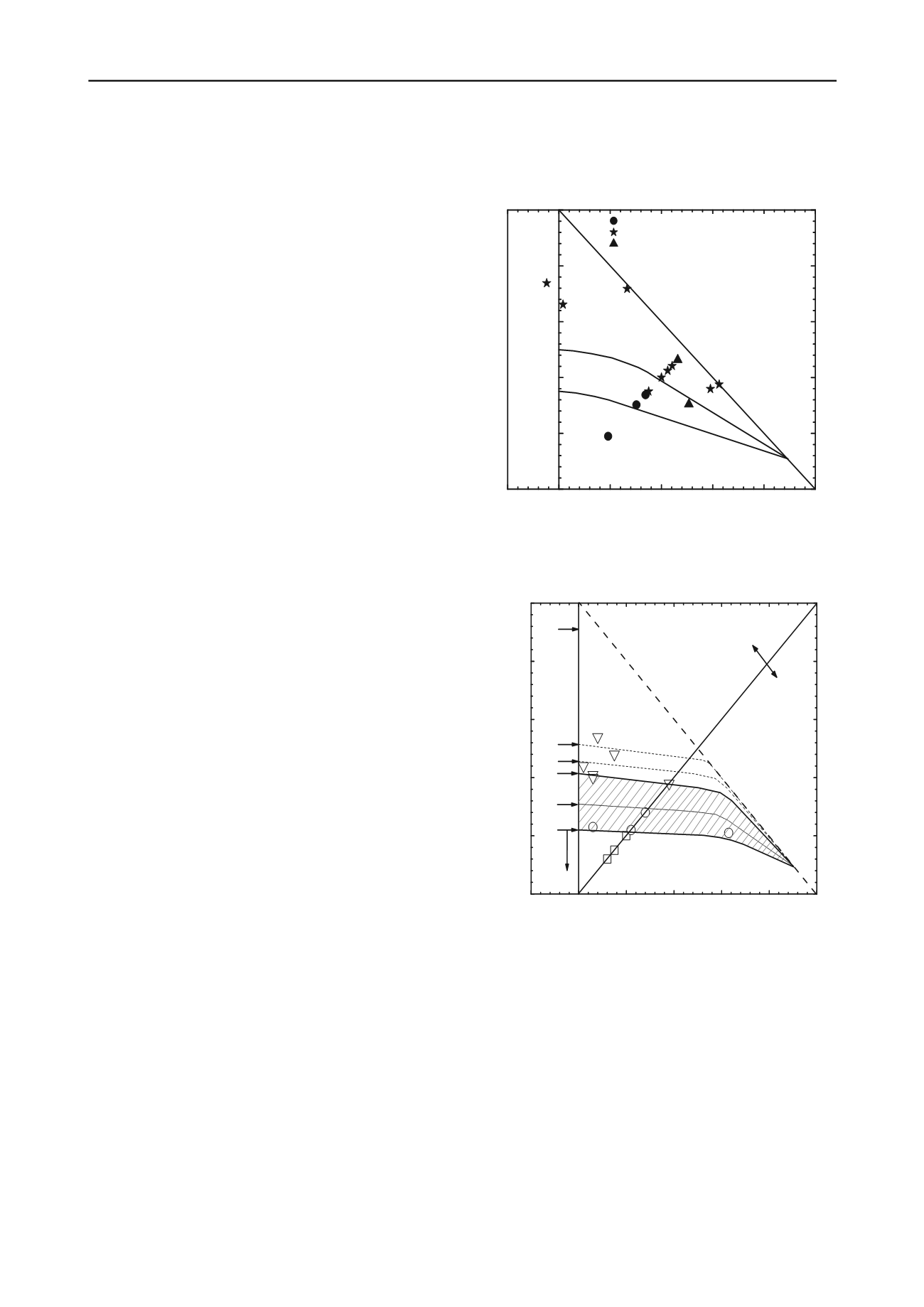
On reproduit sur les Figures 1 et 2 les diagrammes cycliques
obtenus pour les essais de Dunkerque (Jardine and Standing,
2012) et pour les essais en chambre de calibration (Tsuha et al.,
2012).
-0,2 0,0 0,2 0,4 0,6 0,8 1,0
0,0
0,2
0,4
0,6
0,8
1,0
No cyclic failure
First failure
Cyclic failure after previous cyclic or static failure
3
206
24
13
1
12
41
1
9 27
345
>221
>200
Q
cyclic
/Q
T
Q
mean
/Q
T
>1000
Unstable
Metastable
Stable
Figure 1 : Diagramme de stabilité cyclique des pieux battus de
Dunkerque (d’après Jardine and Standing, 2012)
-0,2 0,0 0,2 0,4 0,6 0,8 1,0
0,0
0,2
0,4
0,6
0,8
1,0
One way
Q
cyclic
/Q
T
Q
mean
/Q
T
Two way
Stable
Unstable
>1000
N
f
=
1
10
100
1
4
10
4
1000
500
5
N
f
=number of cycles to failure
Meta-Stable
66
165
580
Figure 2 : Diagramme de stabilité cyclique des pieux modèles en
chambre de calibration (d’après Tsuha et al., 2012)
Pour ces deux diagrammes, la rupture est atteinte lorsque le
déplacement de la tête du pieu atteint 0,1D. La zone
instable
caractérise les essais ayant atteint le critère de rupture avant 100
cycles. La zone
stable
correspond à une zone de faible
amplitude de chargement cyclique dans laquelle les pieux ont
été soumis à plus de 1000 cycles sans accumuler de
déplacements significatifs (pour les deux types de pieux) ou
pour lesquels la vitesse de déplacement était inférieure à 1mm
pour 1000 cycles (pieux de Dunkerque). Entre ces deux zones
se situe une zone qualifiée de
métastable
dans laquelle les pieux
atteignent la rupture entre 100 et 1000 cycles ou développent
des taux de déplacement pouvant faire craindre des ruptures au-
delà de 1000 cycles.


