1731
On the stability of a trap door evaluated by upper bound method
Sur la stabilité d'une trappe évaluée par la méthode de borne supérieure
Kobayashi S., Matsumoto T.
Kanazawa University, Japan
ABSTRACT: It is crucial to evaluate critical configurations of underground structures, such as a width of a structure under various
soil conditions and various depths, and a minimum support force to stabilize underground structures. In this article, for the sake of
simplicity, it is assumed that a trap door with width
D
buried at a certain depth in a modified Cam-clay soil is supported by upward
uniform pressure
q
. A critical pressure
q*
which is necessary to sustain a trap door is evaluated by upper bound method. As a failure
mode of a ground, it is assumed that a parabola-shaped loosened soil zone just above a trap door will fall down vertically. Calculated
results are summarized in charts which will be useful for practical design.
RÉSUMÉ : Il est essentiel d'évaluer les configurations critiques des ouvrages souterrains, tels que la largeur d'une structure dans des
conditions de sol et de profondeur différentes, et une force de soutien minimum pour stabiliser les structures souterraines. Dans cet
article, pour des raisons de simplicité, on suppose que la trappe avec largeur
D
enterré à une certaine profondeur dans une version
modifiée du Cam-Clay argileux est soutenue par la hausse de pression uniforme
q
. Une pression critique
q*
qui est nécessaire pour
maintenir une trappe est évaluée par la méthode de limite supérieure. En tant que mode de défaillance d'un sol, on suppose que la zone
en forme de parabole sol ameubli juste au-dessus d'une trappe va tomber verticalement. Les résultats calculés sont résumés dans les
tableaux qui seront utiles pour la conception pratique.
KEYWORDS: stability, trap door, underground structure, limit analysis, upper bound method, modified Cam-clay model
1 INTRODUCTION
It is crucial to evaluate critical configurations of underground
structures, such as a width of a structure under various soil
conditions and various depths, and a minimum support force to
stabilize underground structures. To this end, in this article,
upper bound analysis to evaluate the critical supporting
pressures of a underground structure is proposed. It will be
demonstrated the importance of a ground arch for the stability
of underground structures, because critical supporting pressures
are depending on the width of a trap door.
2 DISCRIPTION ANE FORMULATION OF A PROBLEM
For the simplicity of a problem, a stability of a underground
structure at its crown will be focused on. In other words, a
possible failure mode such that a crown of a underground
structure and its surrounding soil may fall down, is investigated.
Other members of a underground structure, such as side walls
and an invert, are assumed to have enough strengths to neglect
structural failures at these members.
A soil is modeled as rigid-plastic material obeying Modefied
Cam-clay model and the associated flow rule. It is also assumed
that a soil is under a drained condition and generation and
dissipation of pore water pressures due to deformation of a soil
are neglected.
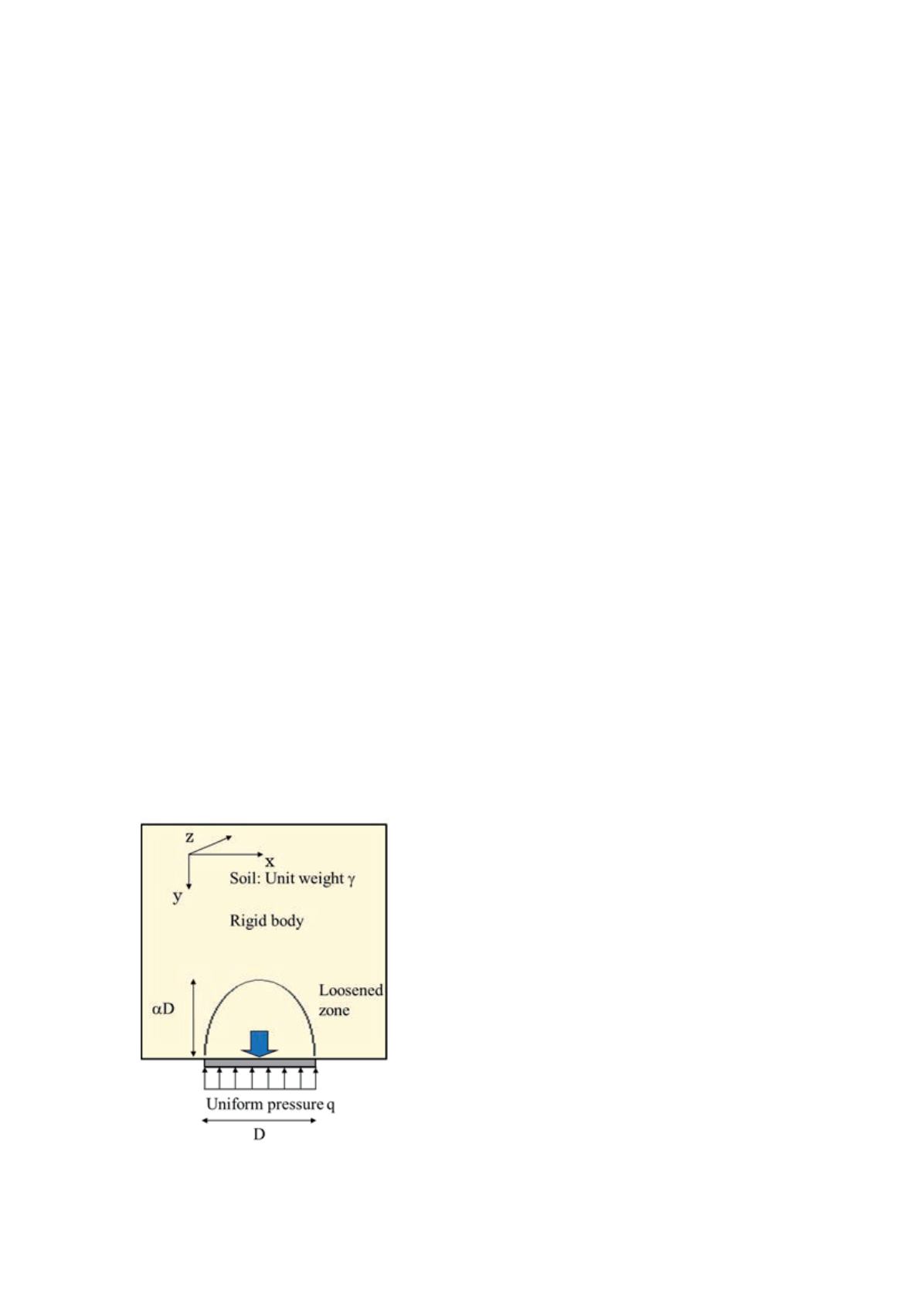
As a crown of a underground structure, it is simply assumed
that a trap door with width D buried at a certain depth in a soil.
To stabilize a trap door and a surrounding soil, a uniform
upward pressure
q
is applied on the surface of a trap door. A
target problem of this study is schematically illustrated in
Figure 1.
2.1 Size and shape of a loosened zone of a soil
A failure mode is assumed in upper bound analysis. Generally
speaking, it is difficult to find precise shape and size of a failure
zone of a soil at the instant of failure. Many case studies show
only shape and size of a failure zone after the event. Therefore,
in this study, a failure zone at the instant of failure is assumed to
be a parabolic shape which crosses at the both end of a trap
door. A vertical coordinate of this parabola is denoted as
y
0
in
Figure 2. This
y
0
stands for the frontier of rigid and plastic
zones. It is also assumed that a soil moves only vertically and its
distributions are linear both in the vertical and horizontal
directions within a parabola as is in Eq. (1).
Figure 1. Assumed failure mode and a loosened soil zone


