1595
Méthode simplifiée de calcul d'une paroi sous séisme
Simplified seismic wall stability analysis
Serratrice J.-F.
CETE Méditerranée, Aix en Provence, France
RÉSUMÉ : Une méthode simplifiée est proposée pour rechercher l'équilibre d'une paroi sous l'action d'efforts sismiques pseudo-
statiques. Le mécanisme de rupture met en jeu deux coins situés de part et d'autre de l'écran dans un profil du massif. L'équilibre d'un
coin est examiné, puis celui de la paroi après avoir évoqué le principe du calcul. Deux exemples sont commentés ensuite. La méthode
trouve un prolongement avec l'introduction de pressions d'eau dans le massif afin de comparer les calculs effectués en contraintes
effectives à ceux effectués en contraintes totales.
ABSTRACT: A simplified method is proposed to find the equilibrium of a wall submitted to seismic induced pseudo-static loads. The
failure mechanism involves two wedges on either side of the wall in a transverse profile. The equilibrium of a wedge is examined first
and then that of the wall, after referring to the principle of calculation. Two examples are discussed then. The method is extended with
the introduction of water pressures in the soil in order to compare effective stresses calculations and total stresses calculations.
KEYWORDS: Wall, pseudo-static equilibrium
1 INTRODUCTION
Le problème de l'équilibre pseudo-statique d'une paroi est traité
ici par une méthode simplifiée d'équilibre de forces. La solution
est recherchée pour une application au cas des massifs de sol
sollicités à court terme en condition non drainée pendant le
temps d'un séisme et pour lesquels la cohésion non drainée
constitue le terme principal de résistance du sol. Le cas d'un
milieu purement frottant est examiné aussi à titre de
comparaison.
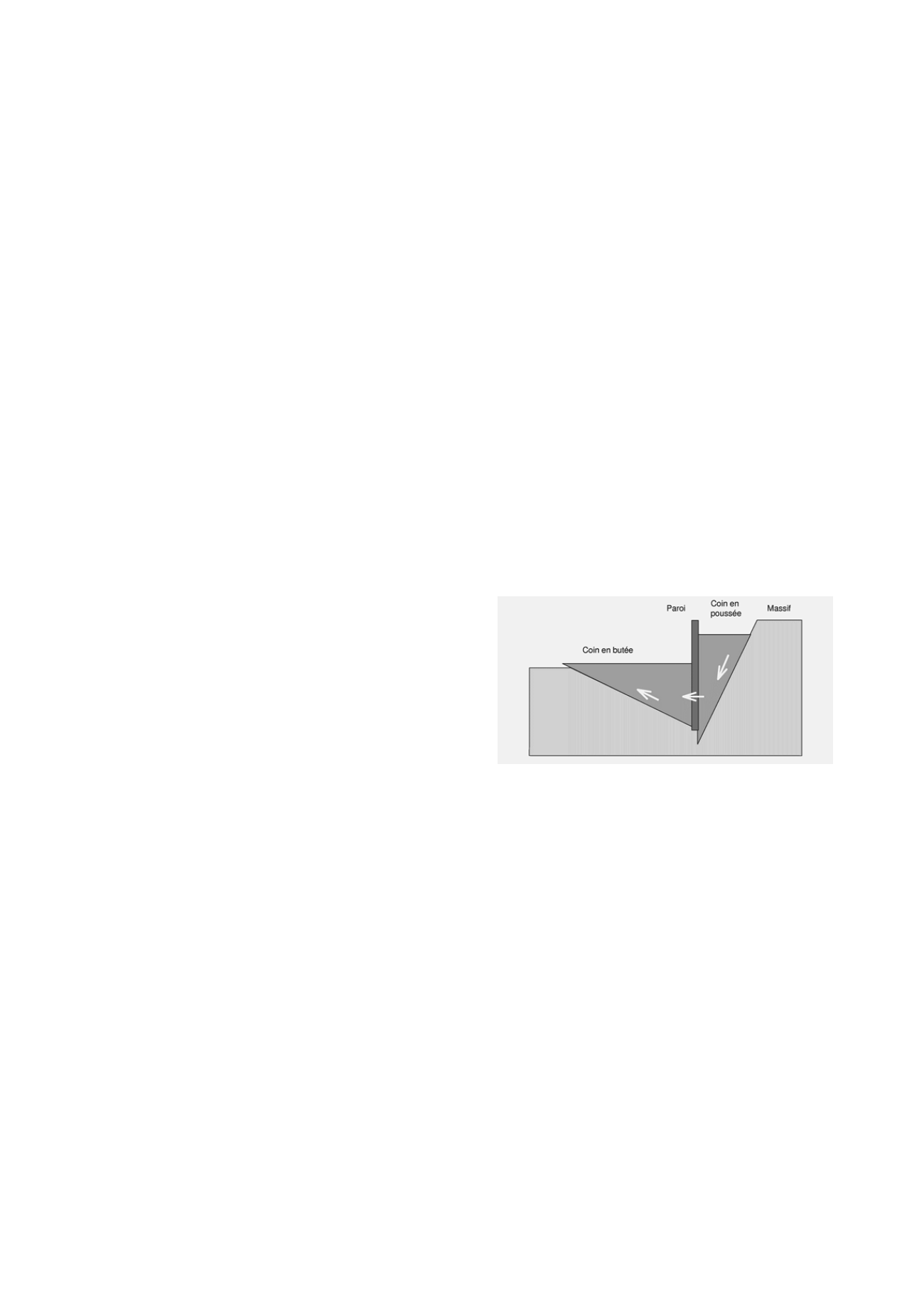
Un mécanisme de rupture simplifié est pris en compte, qui
met en jeu deux coins situés de part et d'autre de l'écran dans un
profil du massif. Le coin amont exerce une poussée sur l'écran.
Le coin aval exerce une butée. Au chargement statique constitué
par le poids propre des coins s'ajoute un chargement pseudo-
statique représenté par deux forces inertielles colinéaires qui
s'appliquent à chacun des coins. La cinématique de rupture se
manifeste par le glissement des coins sur leurs bases qui
constituent une surface de rupture, alors que l'écran vertical est
animé d'un mouvement de translation horizontal, comme
indiqué sur la figure 1. Les flèches montrent la cinématique des
blocs.
2 EQUILIBRE D'UN COIN
2.1 Présentation et hypothèses
Un premier niveau de calcul consiste à considérer un coin de
massif en poussée ou en butée et à chercher l'équilibre des
forces en présence ainsi que l'équilibre de leurs moments
(figure 2). Ces forces sont le poids propre
W
du coin et la force
pseudo-statique d'inertie
U
, la poussée ou la butée
S
apportée
par l'écran et la réaction
R
du massif sur le coin. La solution
dépend des caractéristiques de résistance
T
du sol le long de la
surface de rupture plane AB. Cette résistance est exprimée par
la loi de Coulomb, qui est caractérisée par un effort de
frottement et un effort de cohésion. La variation de pente de la
surface de rupture qui porte le coin (angle
) aboutit à montrer
l'existence d'une poussée maximale et d'une butée minimale.
Figure 1. Mécanisme de poussée et de butée de part et d'autre de la
paroi.
Par hypothèse, le problème de la stabilité est résolu à deux
dimensions dans un profil transversal du massif. Le terrain est
homogène. Aux poids propres des coins s'ajoutent des efforts
inertiels
U
variables en direction (angle
). L'équilibre limite est
atteint sur les surfaces de rupture planes qui portent les coins.
La réaction
S
de la paroi s'exerce au milieu du parement avec un
angle
donné (point D).
2.2 Solution
Le graphique de la figure 2 représente le coin ABC en équilibre
sous l'action des forces en présence dans le repère (A,
i
,
j
). Le
segment AB représente la surface de rupture de pente tg
(
= (
i
,
l
),
l
direction de AB). Le poids volumique du sol
homogène est
. Le poids
W
s'applique au centre de gravité G
du coin, ainsi que l'effort pseudo-statique
U
de direction
u
et de
module connu U (notation :
U
effort, U module,
u
vecteur
unitaire). La direction
u
est donnée par l'angle
= (
i
,
u
)
variable. Le module est une fraction du poids du coin
U = (a
h
/ a
v
) W (rapport des accélérations horizontale et
verticale).
La résultante de
W
et
U
est
P
=
W
+
U
, de direction
p
.
L'action de l'écran vertical sur le coin est
S
, de direction
s
telle
que
= (
i
,
s
). Les efforts
P
et
S
sont en équilibre avec la
réaction
R
du massif. Cette réaction se décompose en un effort
normal
N
et un effort tangentiel
T
,
R
=
N
+
T
. La direction t de


