1596
Proceedings of the 18
th
International Conference on Soil Mechanics and Geotechnical Engineering, Paris 2013
la composante
T
s'oppose au vecteur mouvement
m
. Le module
T de l'effort de cisaillement
T
est lié au module N de
N
par la
loi de Coulomb T = N tg
+ C où
est l'angle de frottement et
C l'effort de cohésion sur la surface de rupture AB.
Figure 2. Équilibre d'un coin. Forces en présence et surface de rupture.
En introduisant un effort extérieur supplémentaire
F
connu
(appliqué en un point F, de direction
f
et de module F),
l'équilibre du coin est donné par l'équation des forces et
l'équation des moments par rapport à l'origine A. En
décomposant la réaction
R
en
N
et
T
au point E sur AB, les
équilibres des moments et des efforts s'écrivent :
P
+
S
+
N
+
T
+
F
=
0
(1)
M
PA
+ M
SA
+ M
NA
+ M
FA
= 0
(2)
qui aboutissent au système suivant, où les modules S et N sont à
déterminer, ainsi qu'à l'expression de la distance AE d = l
AE
:
cos
S – (sin
+ s cos
tg
) N = -x
p
P + s cos
C – x F
f
sin
S + (cos
– s sin
tg
) N = -y P + s sin
C – y F (3)
p
f
d = (-(l
BC
y
p
– 2 l
AC
x
p
) P / 3 + l
AC
cos
S / 2 – M
FA
) / N
où s = 1 en poussée et s = -1 en butée (pour indiquer la direction
t
), l
AB
la distance AB, l
AC
la distance AC et (x
p
, y
p
) et (x
f
, y
f
) les
coordonnées des vecteurs unitaires
p
de
P
et
f
de
F
.
La cohésion peut être nulle (sol frottant) ou constante le long
de la surface de rupture AB. Dans ce cas, le module de la force
de cohésion est C = l
AB
c où l
AB
est la longueur AB et c la
cohésion. La cohésion peut être variable et augmenter avec la
profondeur z depuis la surface libre du massif par exemple,
suivant la relation c = a
cz
z (a
cz
coefficient). Dans ce cas, le
module de l'effort C est C = a
cz
h
2
/ 2 sin
(h = l
AC
).
2.3 Cas particuliers
Seul l'équilibre statique est étudié ici (
U
=
0
). La hauteur du
parement est notée h (h = l
AC
). L'angle
est nul (
= 0). L'effort
extérieur est nul (
F
=
0
). Dans un sol purement frottant (c = 0)
et pour une longueur unitaire de paroi, l'effort de poussée sur
l'écran est donné par la relation S = K
a
v
h, où K
a
= tg
2
(
/4 –
/2) est le coefficient de poussée,
=
/4 +
/2 et
v
la
contrainte verticale à la profondeur z est
v
=
z. Pour z = h/2,
S = K
h
2
/2
a
Dans un sol purement cohérent (
= 0), le système
d'équations se réduit à :
S sin
N = s cos
C
–
cos
N = W +s sin
C
(4)
nte le long de la surface de rupture, si
bien que S = W – 2 s h c.
3 EQUILIBRE DE LA PAROI
'écran est animé par un mouvement de
tra
i caractérisent ce déphasage peuvent être
év
paroi en pied ou en introduisant des
ancrages près de la tête.
.2 Exemple
duisant à l'équilibre de la paroi. Exemple
d'un sol pur
able vers l'aval.
'angle
vaut
= 35 ° dans cette solution.
qui aboutit à la solution S = tg
W + s C / cos
. Si
=
/4,
C =
2 h c, où c est consta
3.1 Principe de calcul
Le calcul simplifié de l'équilibre limite pseudo-statique de la
paroi s'obtient en disposant deux coins en opposition de part et
d'autre de l'écran (figure 1). Par hypothèse, les surfaces de
rupture planes qui portent les coins déterminent la cinématique
de rupture du massif. L
nslation horizontale.
Comme précédemment, mais pour les deux coins, les efforts
U,
dont les modules U sont une fraction du poids W des coins,
sont appliqués aux points G et "tournent" autour de ces points
en fonction de l'angle
= (
i
,
u
). Dans ce cas, la direction
u
est
commune aux deux coins, mais un déphasage peut être introduit
si les paramètres qu
alués en pratique.
Les modules S des efforts de poussée et de butée appliqués
sur la paroi dépendent des angles
et
et des propriétés de
résistance le long des surfaces de rupture dans le massif de sol.
Ces actions
S
de poussée et de butée sont obtenues en
recherchant les propriétés de résistance du sol les plus
appropriées pour assurer un équilibre d'ensemble. Il existe un
maximum de la force de poussée S côté amont et un minimum
de la force de butée S côté aval. Ces deux efforts sont égaux
pour un jeu particulier des propriétés mécaniques du sol, qui est
à rechercher pour justifier de l'équilibre de la paroi. Si les
propriétés de résistance du sol ne permettent pas de réduire ces
efforts, des efforts extérieurs doivent être ajoutés, en admettant
un encastrement de la
3
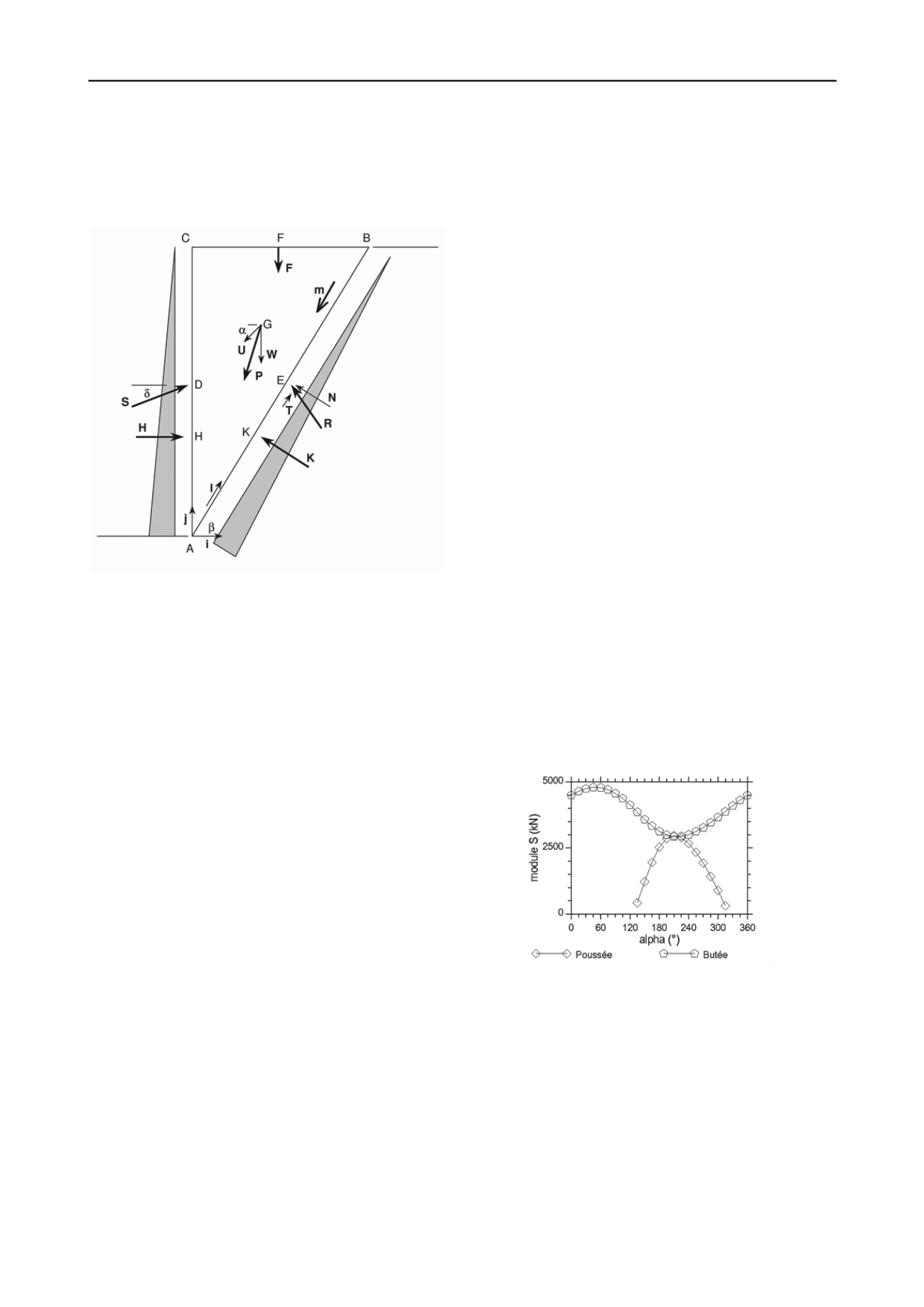
Figure 3. Efforts de poussée et de butée en fonction de l'angle
pour
une résistance du terrain con
ement cohérent.
Les calculs sont effectués avec des angles
(pentes des
plans de rupture) et
(directions des forces d'inertie
U
)
variables. Les caractéristiques de résistance du sol c et
sont
ajustées par tirs et essais successifs pour aboutir à l'égalité des
modules S des poussées et des butées. D'où les caractéristiques
c et
, les angles
et
, puis les différents efforts en jeu. Le
graphique de la figure 3 montre les modules des efforts S de
poussée et de butée en fonction de
lorsqu'un équilibre est
obtenu dans un massif purement cohérent (
= 0). Dans cet
exemple,
= 210 ° approximativement, le vecteur
u
est
légèrement plongeant dans une direction défavor
L
la composante
T
s'oppose au vecteur mouvement
m
. Le module
T de l'effort de cisaillement
T
est lié au module N de
N
par la
loi de Coulomb T = N tg
+ C où
est l'angle de frottement et
C l'effort de cohésion sur la surface de rupture AB.
Figure 2. Équilibre d'un coin. Forces en présence et surface de rupture.
E introduisant un effort extérieur supplémentaire connu
(appliqué en un point F, de direction
f
et de module F),
l'équilibre du coin est donné par l'équation des forces et
l'équation des moments par rapport à l'origine A. En
décomposant la réaction
R
en
N
et
T
au point E sur AB, l
équilibres des moments et des efforts s'écrivent :
P
+
S
+
N
+
T
+
F
=
0
(1)
M
PA
+ M
SA
+ M
NA
+ M
FA
= 0
(2)
qui aboutissent au système suivant, où les modules S et N sont à
déterminer, ainsi qu'à l'expression de la distance AE d = l
AE
:
cos
S – (sin
+ s cos
tg
) N = -x
p
P + s cos
C – x F
f
sin
S + (cos
– s sin
tg
) N = -y P + s sin
C – y F (3)
p
f
d = (-(l
BC
y
p
– 2 l
AC
x
p
) P / 3 + l
AC
cos
S / 2 – M
FA
) / N
où s = 1 en poussée et s = -1 en butée (pour indiquer la direction
t
), l
AB
la distance AB, l
AC
la distance AC et (x
p
, y
p
) et (x
f
, y
f
) les
coordonnées des vecteurs unitaires
p
de
P
et
f
de
F
.
La cohésion peut être nulle (sol frottant) ou constante le long
de la surface de rupture AB. Dans ce cas, le module de la force
de cohésion est C = l
AB
c où l
AB
est la longueur AB et c la
cohésion. La cohésion peut être variable et augmenter avec la
profondeur z depuis la surface libre du massif par exemple,
suivant la relation c = a
cz
z (a
cz
coefficient). Dans ce cas, le
module de l'effort C est C = a
cz
h
2
/ 2 sin
(h = l
AC
).
2.3 Cas particuliers
Seul l'équilibre statique est étudié ici (
U
=
0
). La hauteur du
S sin
N = s cos
C
–
cos
N = W +s sin
C
(4)
nte le long de la surface de rupture, si
bien que S = W – 2 s h c.
3 EQUILIBRE DE LA PAROI
'écran est animé par un mouv ment de
tra
i car ctérisent ce déphasage peuvent être
év
paroi en pied ou en introduisant des
ancrages près de la tête.
.2 Exemple
duisant à l'équilibre de la paroi. Exemple
d'un sol pur
qui aboutit à la solution S = tg
W + s C / cos
. Si
=
/4,
C =
2 h c, où c est consta
3.1 Principe de calcul
Le calcul simplifié de l'équilibr limite pseu o-statique de la
paroi s'obti nt en isposant deux coins en opposition de part et
d'autre de l'écran (fig re 1). Par hypothèse, les surfaces de
rupture planes qui portent les coins déterminent la cinématiq e
de ruptur du massif. L
nslation horizontale.
Comm précédemment, mais pour les deux coins, les efforts
U,
dont les modules U sont une fraction du poids W des coin ,
sont appliqués a x points G et "tournent" autour de ces point
en fonction de l'angle
= (
i
,
u
). Dans ce cas, la irection
u
est
commune aux deux coins, mais un déphasage peut être introduit
si l s paramètres qu
alués en pratique.
Les modules S des efforts de poussée et de butée appliqués
sur la paroi dépendent des angles
et
et des propriétés de
résistance le long des surfaces de rupture dans le massif de sol.
Ces actions
S
de poussée et de butée sont obtenues en
recherchant les propriétés de résistance du sol les plus
appropriées pour assurer un équilibre d'ensemble. Il existe un
maximum de la force de poussée S côté amont et un minimum
de la force de butée S côté aval. Ces deux efforts sont égaux
pour un jeu particulier des propriétés mécaniques du sol, qui est
à rechercher pour justifier de l'équilibre de la paroi. Si les
propriétés de résistance du sol ne permettent pas de réduire ces
efforts, des efforts extérieurs doivent être ajoutés, en admettant
un encastrement de la
3
Figure 3. Efforts de poussée et de butée en fonction de l'angle
pour
une résistance du terrain con
ement cohérent.
Les calculs sont effectués avec des angles
(pentes des
plans de rupture) et
(directions des forces d'inertie
U
)
la composante
T
s'oppose au vecteur mouvement
m
. Le module
T de l'effort de cisaillement
T
est lié au module N de
N
par la
loi de Coulomb T = N tg
+ C où
est l'angle de frottement et
C l'effort de cohésion sur la surface de rupture AB.
Figure 2. Équilibre d'un coin. Forces en présence et surface de rupture.
En introduisant un effort extérieur supplémentaire
F
connu
(appliqué en un point F, de direction
f
et de module F),
l'équilibre du coin est donné par l'équation des forces et
l'équation des moments par rapport à l'origine A. En
décomposant la réaction
R
en
N
et
T
au point E sur AB, les
équilibres des moments et des efforts s'écrivent :
P
+
S
+
N
+
T
+
F
=
0
(1)
M
PA
+ M
SA
+ M
NA
+ M
FA
= 0
(2)
qui aboutissent au système suivant, où les modules S et N sont à
déterminer, ainsi qu'à l'expression de la distance AE d = l
AE
:
cos
S – (sin
+ s cos
tg
) N = -x
p
P + s cos
C – x F
f
sin
S + (cos
– s si
tg
) N = -y P + s sin
C – y F (3)
p
f
d = (-(l
BC
y
p
– 2 l
AC
x
p
) P / 3 + l
AC
cos
S / 2 – M
FA
) / N
où s = 1 en poussée et s = -1 en butée (pour indiquer la direction
t
), l
AB
la distance AB, l
AC
la dista ce AC et (x
p
, y
p
) et (x
f
, y
f
) l
coordonnées des vecteurs u itaires
p
de
P
et
f
de
F
.
La c hésion peut être nulle (sol frottant) ou constante le long
de la surface ruptur AB. Dans ce cas, le module de la force
de cohésion est C = l
AB
c où l
AB
est la longueur AB et c la
cohésion. La cohésion peut être variable et aug enter avec la
profondeur z depuis la surface libre du massif par exemple,
suivant la relation c = a
cz
z (a
cz
coefficient). Dans ce cas, le
module de l'effort C est C = a
cz
h
2
/ 2 sin
(h = l
AC
).
2.3 Cas particuliers
Seul l'équilibre statique est étudié ici (
U
=
0
). La hauteur du
parement est notée h (h = l
AC
). L'angle
est nul (
= 0). L'effort
extérieur est nul (
F
=
0
). Dans un sol purement frottant (c = 0)
et pour une longueur unitaire de paroi, l'effort de poussée sur
l'écran est donné par la relation S = K
a
v
h, où K
a
= tg
2
(
/4 –
/2) est le coefficient de poussée,
=
/4 +
/2 et
v
la
contrainte verticale à la profondeur z est
v
=
z. Pour z = h/2,
S = K
h
2
/2
a
Dans un sol purement cohérent (
= 0), le système
d'équations se réduit à :
S sin
N = s cos
C
–
cos
N = W +s sin
C
(4)
nte le long de la surface de rupture, si
bien que S = W – 2 s h c.
3 EQUILIBRE DE LA PAROI
'écran est animé par un mouvement de
tra
i caractérisent ce déphasage peuvent être
év
paroi en pied ou n introduisant des
ancrages près de la tête.
.2 Exemple
duisant à l'équilibre de la paroi. Exemple
d'un sol pur
able vers l'aval.
'angle
vaut
= 35 ° dans cette solution.
qui aboutit à la solution S = tg
W + s C / cos
. Si
=
/4,
C =
2 h c, où c est consta
3.1 Principe de calcul
Le calcul simplifié de l'équilibre limite pseudo-statique de la
paroi s'obtient en disposant deux coins en opposition de part et
d'autre de l'écran (figure 1). Par hypothèse, les surfaces de
rupture planes qui portent les coins déterminent la cinématique
de rupture du massif. L
nslation horizontale.
Comme précédemment, mais pour les deux coins, les efforts
U,
dont les modules U sont une fraction du poids W des coins,
sont appliqués aux points G et "tournent" autour de ces points
en fonction de l'angle
= (
i
,
u
). Dans ce cas, la direction
u
est
commune aux deux coins, mais un déphasage peut être introduit
si les paramètres qu
alués en pratique.
Les modules S des efforts de poussée et de butée appliqués
sur la paroi dépendent des angles
et
et des propriétés de
résistance le long des surfaces de rupture dans le massif de sol.
Ces actions
S
de poussée et de butée sont btenues en
recherchant les propriété de résista ce du sol les plus
approprié s pour assurer un équilibre d'ensemble. Il existe un
maximum de la force de poussée S côté amont et un mi imum
de la force de butée S côté av l. Ces deux efforts sont égaux
pour un jeu particulier d s propriétés mécaniques du sol, qui est
à rechercher pour justifier de l'équilibre de la paroi. Si les
propriétés de résistance du s l ne permettent pas de réduire ces
efforts, des efforts extérieurs doiven êt e ajoutés, en adm ttant
un ncastrement de la
3
Figure 3. Efforts de poussée et de butée en fonction de l'angle
pour
une résistance du terrain con
ement cohérent.
Les calculs sont effectués avec des angles
(pentes des
plans de rupture) et
(directions des forces d'inertie
U
)
variables. Les caractéristiques de résistance du sol c et
sont
ajustées par tirs et essais successifs pour aboutir à l'égalité des
modules S des poussées et des butées. D'où les caractéristiques
c et
, les angles
et
, puis les différents efforts en jeu. Le
graphique de la figure 3 montre les modules des efforts S de
poussée et de butée en fonction de
lorsqu'un équilibre est
obtenu dans un massif pure ent cohérent (
= 0). Dans cet
exemple,
= 210 ° approximativement, le vecteur
u
est
légèrement plongeant dans une direction défavor
L


