1585
Technical Committee 203 /
Comité technique 203
2.4
Discrétisation dans le temps
Le modèle aux éléments finis et la non linéarité du sol
demandent une discrétisation dans l'espace et dans le temps,
pour permettre la résolution du problème. La loi de
comportement incrémentale est linéarisée à chaque pas de
temps. L'équation (1) est donc exprimée comme
(3)
i
i
i
i
k
k
k
k
M D C D K D F
k
où l'indice
k
indique le pas de temps et
i
indique l'itération du
processus de convergence à la solution. À chaque pas de temps
k
, l'équation (3) nécessite une résolution itérative, pour corriger
la matrice de rigidité
. Le processus de correction continue
jusqu'à que la différence entre deux approximations successives
se réduise à une tolérance fixée (Mestat 1993 et 1998). Le pas
suivant est ensuite analysé.
k
t
i
k
K
L’algorithme de Newmark, une approche implicite utilisée pour
problèmes dynamiques, permet la résolution pas-à-pas
(Newmark 1959; Hughes 1987). Les deux paramètres
et
0.3025
0.6
assurent la stabilité inconditionnelle du
processus d'intégration et une dissipation numérique qui atténue
les modes à fréquence plus élevée (Hughes 1987).
3 COMPARAISON ENTRE 1D-3C ET 1D-1C
La réponse sismique d'un sol horizontal multicouche à la
propagation d'un signal à trois composantes (approche 1D-3C)
est comparée à la superposition des effets des trois composantes
propagées de façon indépendante (approche 1D-1C).
Les enregistrements du mouvement du sol en surface pendant le
séisme de Tohoku du 11 Mars 2011 (magnitude 9), et la
stratigraphie des profils de sol sont fournies par le réseau
accélérométrique K-Net. Les trois composantes du mouvement
enregistré, Nord-Sud, Est-Ouest et Verticale, sont appelées
respectivement
x
, et dans le modèle proposé.
y
z
La comparaison entre les enregistrements et les signaux
numériques 1D-3C est montrée en termes de module de
l'accélération en surface sur la Figure 2, pour le profil de sol
FKS011 (Tableaux 1 et 2). Le mouvement incident est le signal
enregistré sur rocher affleurant, c'est-à-dire à la surface du profil
de type roche FKS015, ensuite divisé par deux (Tableau 1).
a) b)
Figure 2. Module de l'accélération pendant le séisme de Tohoku : signal
enregistré et numérique en surface (a); signal d'entré au rocher et signal
numérique en surface (b), dans le cas FKS011/FKS015.
Tableau 1. Profil de sol et profil de type roche sélectionnés dans la
égion de Tohoku (Japan).
r
Nom du site
Iwaky
Tanagura
Préfecture
Fukushimaken Fukushimaken
Code du site
FKS011
FKS015
Distance épicentre
206
250
Profondeur H (m)
10.00
10.03
v
s
moyenne (m/s)
222
463
min {v
p
/ v
s
}
3.05
-
La comparaison entre les approches 1D-1C and 1D-3C est
montrée en termes d'histoire temporelle en surface sur la
Figure 3. Le signal incident en termes de module de
l'accélération arrive amplifié à la surface du profil de sol
analysé pour les deux approches 1D-1C et 1D-3C, mais le pic
est réduit dans le cas 1D-3C et approxime mieux les
enregistrements (Fig. 3).
Tableau 2. Stratigraphie et propriétés du sol pour le profil FS011.
FKS011 z
(m)
H
i
(m)
(kg/m
3
)
v
s
(m/s
)
v
p
(m/s
)
r
(
‰
)
Sol sup.
2.2 2.2 1430 100 700 0.800
3 0.8 1650 210 700 0.427
4
1 1720 210 1300 0.427
Limon
5.95 1.9
5 1660 330 1300 0.427
Argile 6.85 0.9 1810 330 1300 2.431
8 1.1
5 1970 330 1300
100
9
1 1980 590 1800 100
Roche
10 1 2060
590 1800
100
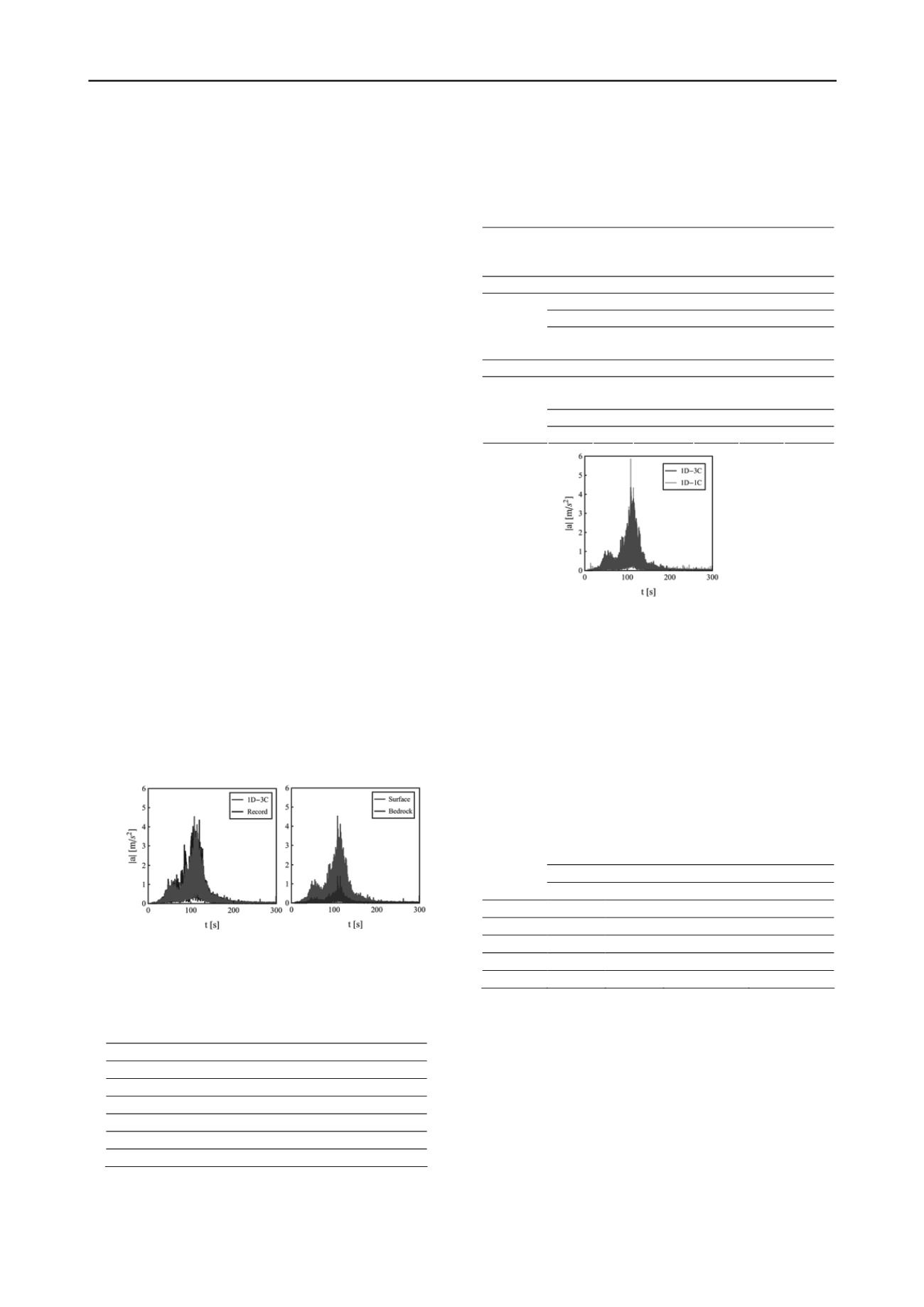
Figure 3. Module de l'accélération en surface pendant le séisme de
Tohoku : résultats 1D-3C et 1D-1C pour le cas FKS011/FKS015.
La réponse locale du profil de sol FKS011 à un séisme à trois
composantes est analysée par les profils avec la profondeur du
module maximum d'accélération et de vitesse, de contraintes et
déformations octaédriques et par boucles déformation-
contrainte dans la couche plus déformée (Fig. 4). Les
accélérations maximales (Tableau 3) et les vitesses sont plus
élevées pour la combinaison de trois propagations 1C (approche
1D-1C). Les contraintes maximales sont réduites dans le cas
1D-3C et dans les couches plus souples les déformations
maximales peuvent être plus élevées (Fig. 4).
Tableau 3. Accélérations enregistrées pendant le séisme de Tohoku en
haut du profil de sol FKS011 et du profil de type roche FKS015 (signal
'entrée) et accélérations calculées en haut du profil de sol FKS011.
d
Enregistrements
1D-3C
1D-1C
Sol
Roche
Sol/Roche
Profil
FKS011 FKS015
FKS011/FKS015
a
x
(m/s
2
)
3.74
1.36
3.78
3.97
a
y
(m/s
2
)
3.12
1.01
3.92
4.33
a
z
(m/s
2
)
3.00
0.58
1.64
0.89
|a| (m/s
2
)
4.47
1.42
4.55
5.72
La courbe déformation-contrainte de cisaillement de premier
chargement (Fig. 4) est obtenue, dans le cas de propagation 1C,
par la courbe de réduction du module de cisaillement. Quand les
déformations de cisaillement sont plus élevées que la limite
élastique, on observe, sous chargement cyclique, des boucles
dans le plan déformation-contrainte, avec hystérésis. La réponse
cyclique du sol en termes de contrainte et déformation de
cisaillement dans la direction
x
, dans les deux cas de signal
d'entrée à trois composantes (1D-3C) et de propagation de la
seule composante
x
du signal (1D-1C) est comparée sur la
Figure 4. En passant d'une à trois composantes, pour une
déformation de cisaillement maximale fixée, le module de
cisaillement diminue et la dissipation augmente. La résistance
du matériau est inférieure dans le cas de chargement 3D plutôt
que dans le cas de cisaillement simple, représenté par la courbe


