1584
Proceedings of the 18
th
International Conference on Soil Mechanics and Geotechnical Engineering, Paris 2013
une composante, dans l'intervalle de déformation non linéaire
stable. Dans le cas de chargement à trois composantes, pour une
même gamme de déformations, la forme des boucles
d'hystérésis change à chaque cycle. Les boucles d'hystérésis
pour chaque direction horizontale sont altérées par l'interaction
entre les composantes de chargement.
La différence principale entre la superposition des effets de trois
mouvements de terrain à une composante (approche 1D-1C) et
le modèle de propagation 1D-3C est analysée en termes
d'histoire temporelle du mouvement, contrainte maximale et
comportement hystérétique, avec plus de non linéarité et d'effets
de couplage entre les composantes. Cet effet est plus évident
pour petits rapports entre la vitesse des ondes de cisaillement et
pression dans le sol et grands rapports entre le pic des
composantes verticale et horizontale de l'onde incidente.
L'objectif de cette recherche est de confirmer, en utilisant des
données réelles, les résultats de l'analyse paramétrique faite en
utilisant des signaux synthétiques. La propagation simultanée de
trois composantes du mouvement sismique (1D-3C) est
comparée avec la superposition des effets de trois propagations
d'une seule composante du mouvement (1D-1C), dans des
profils de sol de la région de Tohoku (Japon), pour comprendre
l'influence d'un trajet de chargement 3D et de la polarisation de
l'onde incidente. On a utilisé des signaux sismiques ayant un
rapport entre les pics en accélération verticale et horizontale
supérieur à 70%, pour comprendre l'influence d'une composante
verticale importante. L'influence des propriétés du sol et des
ondes sismiques incidentes sur la réponse locale sont discutées.
2 MODÈLE DE PROPAGATION 1D-3C
Les trois composantes du mouvement sismique sont propagées
dans un profil de sol, à comportement non linéaire, à partir de
l'interface entre le bassin sédimentaire et le rocher sous-jacent, à
comportement élastique. On suppose que le sol multicouche est
infiniment étendu suivant les directions horizontales. Les ondes
de cisaillement et de pression se propagent verticalement dans
la direction . Ces hypothèses conduisent à ne pas avoir de
variation de déformation dans les directions
z
x
et . Le sol est
supposé être un milieu continu et homogène, à chaque
profondeur, en régime de petites déformations.
y
2.1
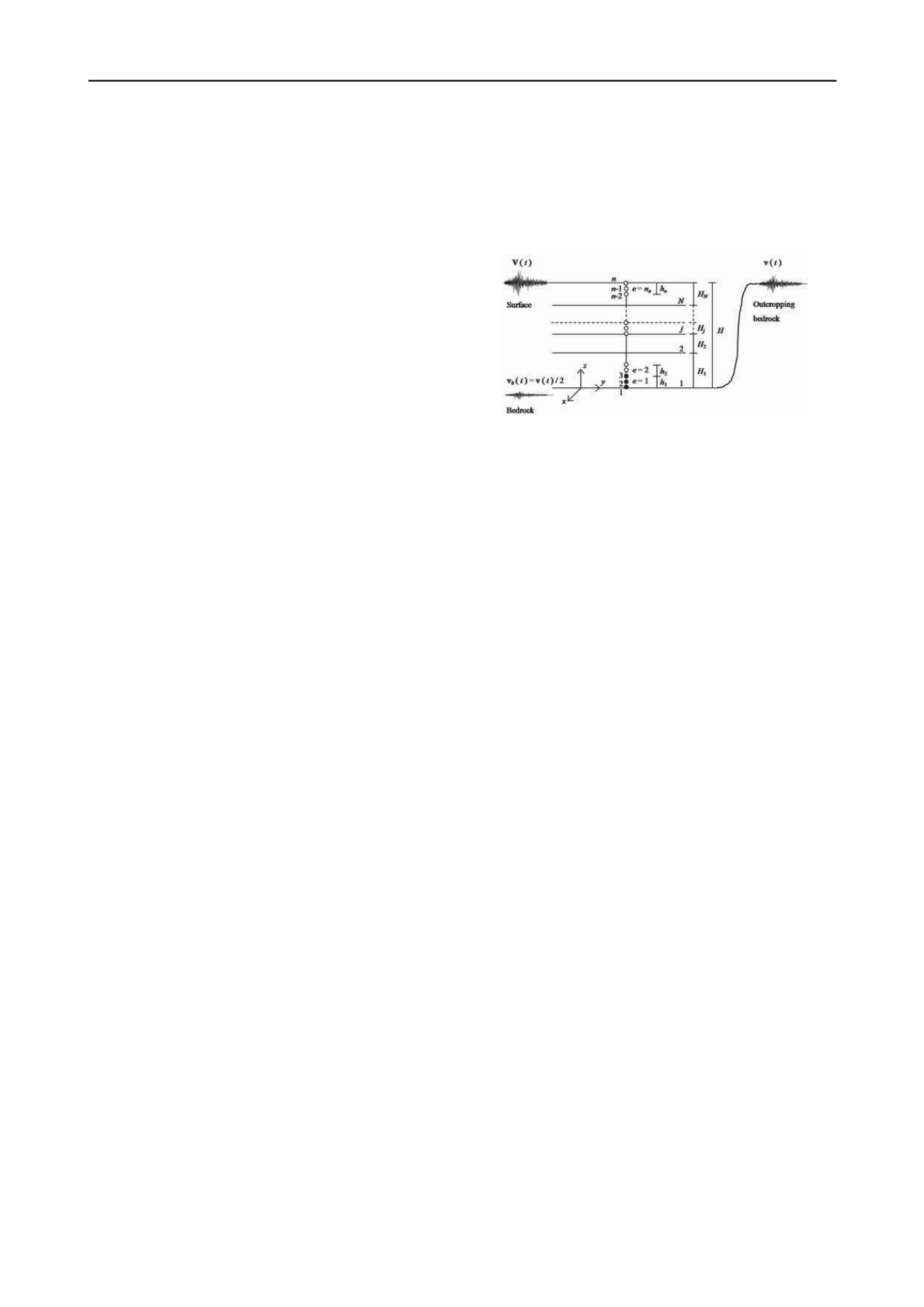
Discrétisation spatiale
La stratification de couches horizontales, parallèles au plan
xy
,
est discrétisée en utilisant un schéma de type éléments finis
(Fig. 1). On a adopté des éléments quadratiques linéiques à trois
nœuds. En accord avec le modèle aux éléments finis, l'équation
d'équilibre discrète s’écrit sous forme matricielle
int
MD CD F F
(1)
où est la matrice de masse, et sont les vecteurs vitesse
et accélération, respectivement, c'est-à-dire la première et la
deuxième dérivée dans le temps du vecteur de déplacement .
est le vecteur des forces internes nodales. Le vecteur des
charges et la matrice de dissipation sont non nuls quand
on utilise une condition à la limite absorbante et ils sont nuls
quand on impose le mouvement enregistré en profondeur
comme condition à la limite.
M
t
D
D
D
in
F
F
C
Le problème différentiel d'équilibre (1) est résolu en accord
avec les conditions de compatibilité et l'hypothèse de variation
de déformation nulle dans les directions horizontales, avec une
loi de comportement 3D non linéaire cyclique et avec les
conditions aux limites décrites de suite.
La discrétisation de la colonne de sol en
e
n
éléments
quadratiques linéiques et donc en
nœuds (Fig. 1), qui
ont trois degrés de liberté chacun, implique un vecteur de
déplacement de dimension
, composé par trois blocs dont
les termes sont les déplacements des
nœuds dans les
directions
2 1
e
n n
n
D
3
n
x
,
et , respectivement. Les propriétés du milieu
sont constantes dans chaque élément fini et dans chaque couche
de sol. L'assemblage des matrices de dimension
et des
vecteurs de dimension
est fait de façon indépendante pour
les trois sous-matrices de dimension
et pour les trois
sous vecteurs de dimension , respectivement, correspondant
aux directions de mouvement
y
z
3 3
n n
3
n
n n
n
x
, et .
y
z
Figure 1. Discrétisation spatiale d'un bassin sédimentaire horizontal
multicouche secoué à la base par un séisme à trois composantes,
enregistré sur rocher affleurant et divisé par deux.
2.2
Conditions aux limites
Le système de couches de sol horizontales est limité en haut par
la surface libre où on suppose nulles les contraintes normales.
Le rocher à la base est modélisé comme un milieu élastique
semi-infini. La condition à la limite suivante, appliquée à
l'interface sol-rocher, permet à l'énergie d'être réfractée dans le
milieu sous-jacent (Joyner et Chen 1975, Joyner 1975, Bardet et
Tobita 2001), en tenant compte d'une rigidité finie du rocher:
2
T
b
p σ
v
c v
(2)
Les contraintes normales à la base de la colonne de sol à
l'interface sol-rocher sont
p
et
c
est une matrice diagonale
de dimension
T
σ
3 3
dont les termes sont
,
et
.
Les paramètres
b s
v
b
b sb
v
b pb
v
b
,
sb
v
et
sont la densité du rocher et la
vitesse des ondes de cisaillement et de compression dans le
rocher, respectivement. Les trois termes des vecteurs et
sont, respectivement, les vitesses inconnues à l'interface sol-
rocher (nœud 1 dans la Fig. 1) et les données d'entrées en termes
de vitesses des ondes dans le milieu élastique sous-jacent, dans
les directions
pb
v
v
b
v
x
,
et . L'onde incidente à trois composantes
peut être obtenue en divisant par deux les enregistrements
sismiques au rocher affleurant (Fig. 1), en considérant l'effet de
surface libre dans la roche supposée élastique linéaire.
y
z
b
v
Si on utilise les enregistrements en profondeur, contenant des
ondes incidentes et réfléchies, dans ce cas le mouvement à
l'interface sol-rocher (nœud 1 dans la Fig. 1) est connu et
imposé comme condition à la limite.
2.3
Modèle de comportement 3D non linéaire cyclique
Le modèle rhéologique de Masing-Prandtl-Ishlinskii-Iwan
adopté pour les sols a été sélectionné car il est tridimensionnel
avec comportement non linéaire en charge et en décharge et
surtout parce que le seul paramètre nécessaire pour caractériser
le comportement hystérétique du sol est la courbe de réduction
du module de cisaillement
G
avec la déformation de
cisaillement
. C'est un mécanisme à plusieurs surfaces de
plasticité pour sol sec, utilisé dans un intervalle de déformation
de non linéarité stable. Les taux de déformation plus élevés ne
sont pas bien représentés sans prendre en compte les conditions
de sol non drainé.


