1409
Technical Committee 203 /
Comité technique 203
Table 2. Modelling parameters of the SYS Cam-clay model
Elasto-plastic parameters
Minimum value
0.0025
Compression index
λ
Maximum value
0.05
Reference value of
γ
p
for
λ γ
λ
0.0001
Minimum value
0.0015
Swelling index
κ
Maximum value
0.049
Reference value of
γ
p
for
κ
γ
κ
0.01
Critical state constant
M
0.90
Specific volume at q = 0 and p ’= 98.1 kPa on NCL
N
1.785
Poisson’s ratio
0.264
Cohesion (kPa)
8 0
4 ANALYTICAL RESULT
4.1
FEM
Figure 7 shows analytical and test results of lateral response
acceleration and displacement at observation points shown in
Figure 8 (a). The analytical results are largely consistent with
the test results. Figure 8 (b) to (d) shows distributions of
amplitude of lateral response acceleration and maximum
shear strain when the amplitude of lateral response
acceleration is the minimum. In test results, the lateral
response acceleration is amplified at the top and right hand
side slope as shown in Figure 8 (b). Large amplification of
the lateral response acceleration is produced at middle part
of the right hand side slope, where partial catastrophic failure
occurred (see Figure 2 (a)). On the other hand, although the
analysis can describe overall behavior of amplification and
phase lag of lateral response acceleration as shown in Figure
8 (c), that cannot describe localized amplification of lateral
response acceleration at right hand side slope shown in
Figure 8 (b) seen in test. Also, shear strain growth is
prominent at the toe of right hand side slope as shown in
Figure 8 (d), which is inconsistent with a middle part of the
slope where partial catastrophic failure occurred. This
indicates that the used FEM model is applicable to describe
overall behavior of amplification and phase lag of lateral
response acceleration, but the model has problems to solve to
deal with shear strain growth due to localized amplification
of lateral response acceleration.
4.2
MPM
Figure 9 and Figure 10 show processes of distributions of
maximum shear strain and lateral response acceleration
derived from MPM analysis. In one layered model,
analytical results show catastrophic failure at right hand side
slope, but the amount of deformation is overestimated
comparing to test results. In three layered model, final
configuration derived from the analysis is largely consistent
with that of the test. Figure 11 shows time histories of lateral
and vertical response displacement at observation points
displayed in Figure 10 (a) introduced from test and analysis.
Start time and rate of change of displacement derived from
the analysis is largely consistent with that in the test. These
indicate that the MPM analysis can deal with the large
deformation such as slide down although a constitutive law
was modeled up to residual state as shown in Figure 6.
5 CONCLUSION
Seismic behavior of large-scale slope model on the world’s
largest shaking table test was analyzed by FEM and MPM.
The outcomes can be summarized as follows:
1) The same trend of the amplification and phase lag of
response acceleration at the top of slope of one layered slope
model as that seen at the shaking table test could be obtained
by the FEM with GHE-S model together with the multiple
nonlinear spring models. However, the FEM model could
not describe the localized amplification of response
acceleration and shear strain growth at the middle part of the
slope where partial catastrophic failure occurred.
0.000001 0.00001 0.0001 0.001
0.01
0.1
0
0.2
0.4
0.6
0.8
1
0
0.1
0.2
0.3
0.4
0.5
G/G
0
減衰
, h
実験値
解析値
Model
Test
h
0.000001 0.00001 0.0001 0.001
0.01
0.1
0
0.2
0.4
0.6
0.8
1
0
0.1
0.2
0.3
0.4
0.5
G/G
0
減衰
, h
実験値
解析値
Model
Test
h
(a) General part (b) Reinforced part
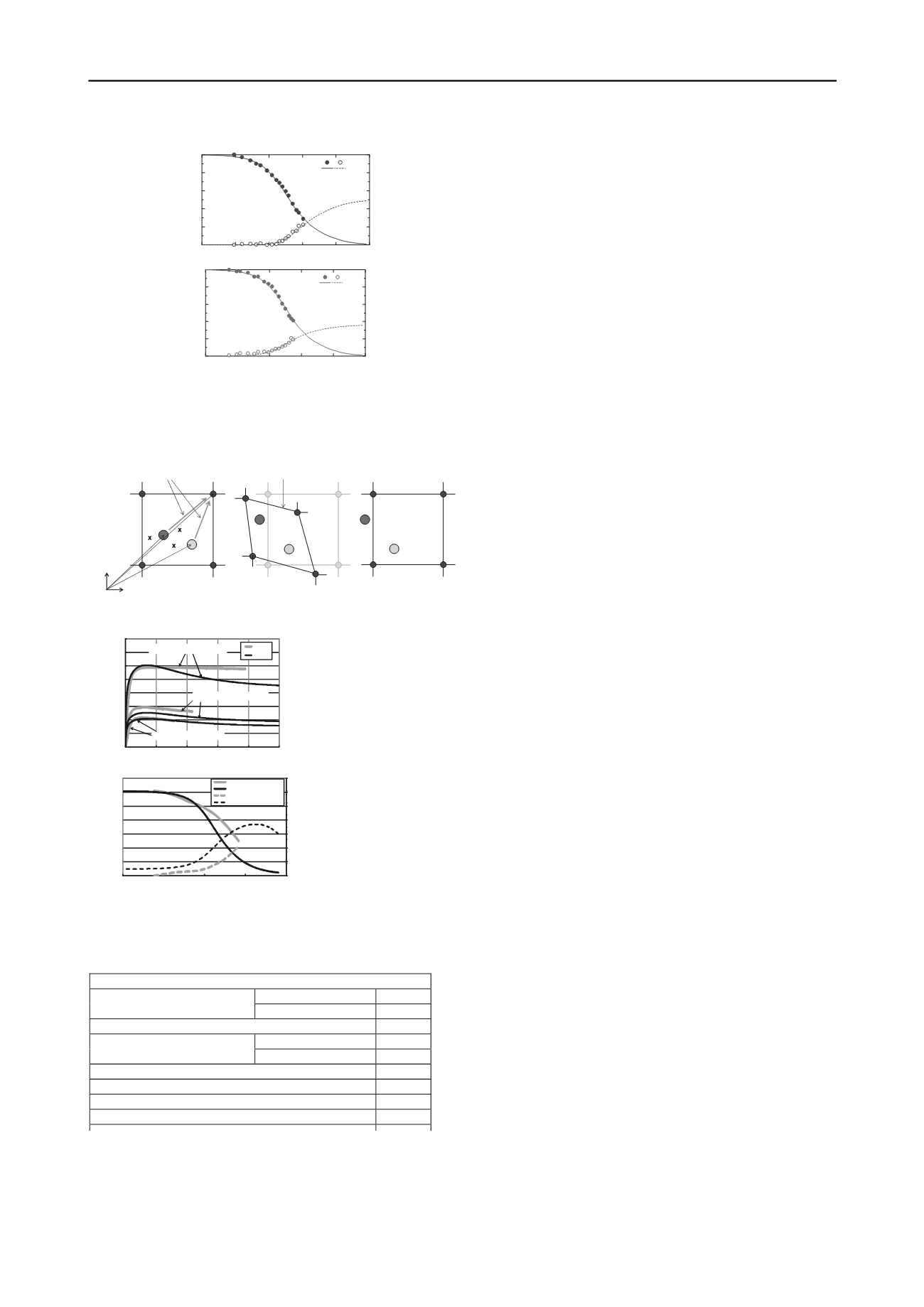
Figure 4. Results of investigation to determine the stress-strain
characteristics of a material specimen under cyclic tri-axial tests using the
GHE-S model
y
x
x
i
x
p1
x
p2
(a)Formerstage
(b)Conventionstage
(c)Latterstage
Transfer physical values of particles
to nodes of background mesh
Calculate strain of background mesh
usingconservativeFEM approach
Mesh is reset to the initial configuration,
whiletheparticlekeepsthe position.
Figure 5. Analysis flow of the MPM
0.0
20.0
40.0
60.0
80.0
100.0
120.0
140.0
160.0
0.0
2.0
4.0
6.0
8.0
10.0
D
eviatoric
stress
(kP
a)
Axialstrain (%)
Test
Model
Confining pressure= 50kPa
Confining pressure=5kPa
Confiningpressure =10kPa
0
5
10
15
20
25
30
35
40
0
10
20
30
40
50
60
70
0.0001
0.0010
0.0100
0.1000
1.0000
D
am
ping
ratio
h
(%
)
S
hearm
odulus
G
(M
N
/m
2
)
Deviatoricstrain (%)
Experiment (shear modulus)
Analysis (shearmodulus)
Experiment (damping ratio)
Analysis (damping ratio)
Confiningpressure= 10kPa
Figure 6. Results of investigation to determine the stress-strain
characteristics of a material specimen under tri-axial compression tests and
cyclic tri-axial tests using the SYS Cam-clay model
2) The similar failure patterns of one and three layered slope
models to that seen at the shaking table test could be obtained
by the MPM with the SYS Cam-clay model. However, the
MPM analysis could not produce good agreements in the one
layered slope model regarding the amount of deformation,
which should be improved in the future work.
3) Consequently, it is considered that the FEM analysis is
appreciate for a slope with large amplification of response
acceleration and the MPM analysis is appreciate for a slope
with a weak layer as analytical tools for assessing seismic
safety of slopes. However, both models should be improved
to evaluate seismic behavior of slopes more accurately.


