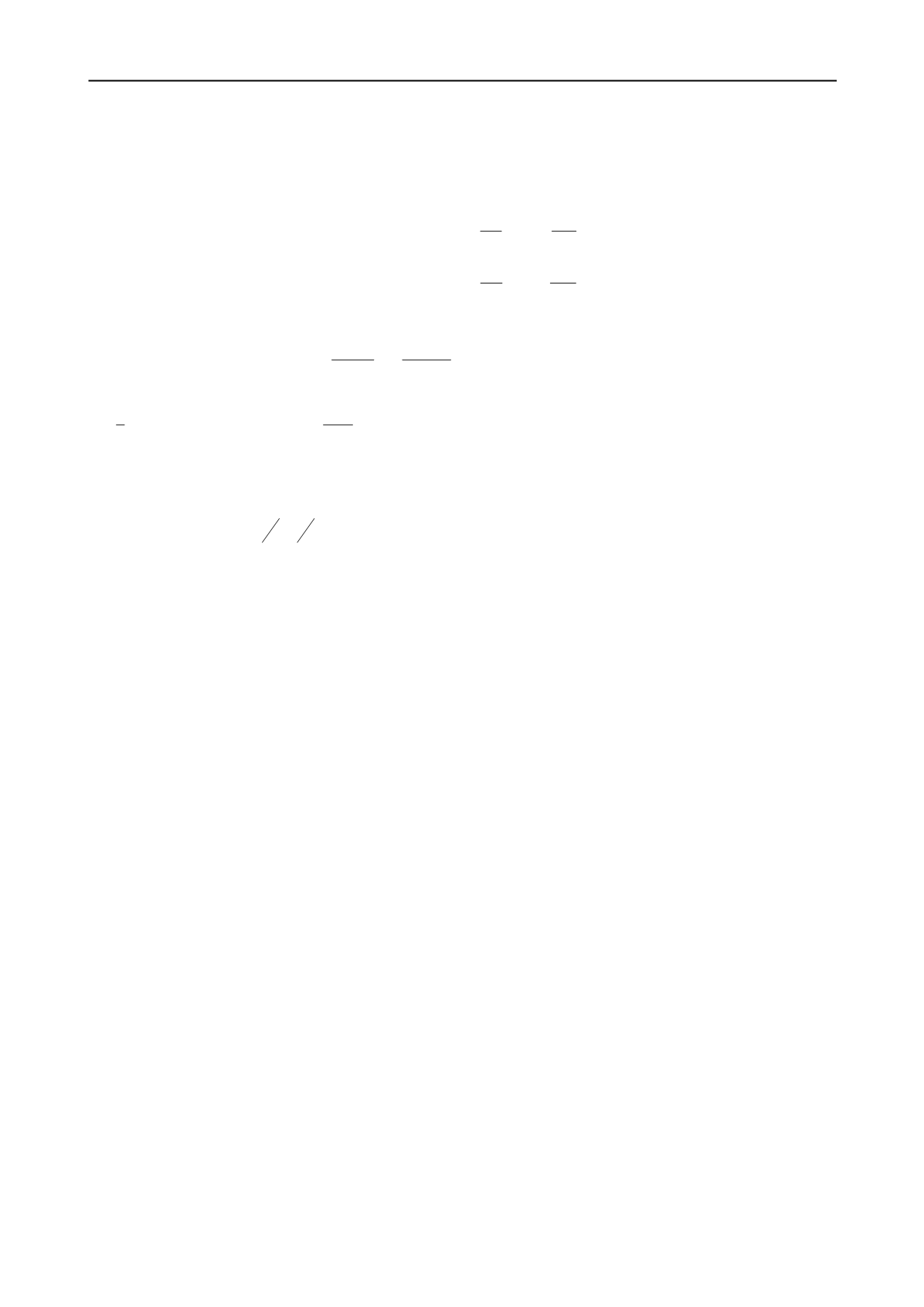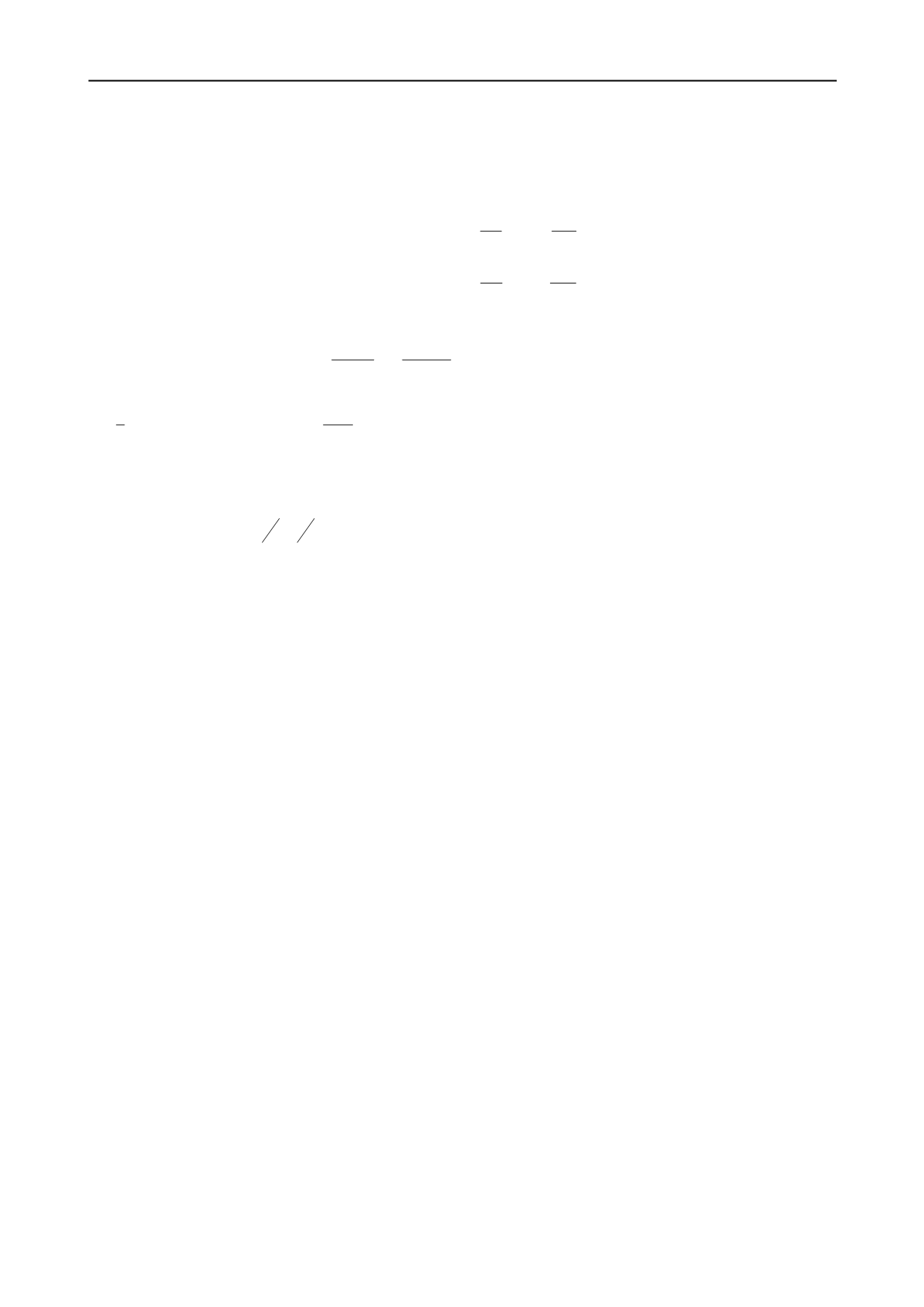
704
Proceedings of the 18
th
International Conference on Soil Mechanics and Geotechnical Engineering, Paris 2013
,
n
n
ij
j i
c
(3)
In this paper, the single hardening elasto-plastic Lade’s
model (Kim and Lade 1988, Lade and Kim 1988), enhanced
with Cosserat rotations and couple stresses, (Ebrahimian et al.
2012), is used. The model has a non-linear elasticity function
and assumes non-associative flow rule and high non-linear
plastic work-based hardening function. The enhancement is
carried out through the second stress and deviatoric stress
invariants in order to incorporate the effects of characteristic
length of micro-structure and couple stresses:
2
2
2
2
2
2
1
2
12
21
2
11 22
33
22
11 33
2
2
m m
J
l
(4)
1 2
12 21
11 22
11 33
22 33
2
1
2
II
m m
I
l
(5)
where,
σ
ij
= stresses;
m
i
= couple stresses; and
l
= material
characteristic length. In 2D Cosserat continuum, the stress
tensor is expressed in the following vector form:
1
2
11 22 33 12 21
T
m m
l
l
(6)
It is worth mentioning here that the stress vector is a non-
symmetric vector due to the effect of couple stresses. Similarly,
the objective strain vector, including strain and micro-curvature
of rotations, is non-symmetric and given by
11
22
33
12
21
1
2
T
l
l
(7)
In finite element implementation, each node in the plane
strain Cosserat continuum will have the following degrees of
freedom:
1
2
3
Tc
U u u
(8)
The constitutive relations used in the current work are
homogenous in time (time-independent behavior); however,
dimensionless time representation is used to avoid using the
differential representation; hence, the following constitutive
laws can be used:
D
(9)
where, [D] = elasto-plastic stiffness matrix in terms of both
stresses and couple stresses. The present micro-polar Lade’s
single hardening model is implemented in a finite element
program in order to investigate the phenomenon of shear
localization in granular soil.
3 FINITE ELEMENT FORMULATIONS
Incorporating the Cosserat couple stresses and rotations, the
virtual work equation in an updated Lagrangian reference is
written as
1
1
1
1
n
n
n
n
n
n
ij
n ij
i
n i
V
S
m dV
1
R
(10)
where,
S
ij
= the second Piola-Kirchhoff stress; and R =
external virtual work. For finite element implementation, a
quadrilateral isoparametric 4-noded element with nodal
displacement and rotational degrees of freedom is formulated
for plane strain condition. Geometric non-linearity is considered
for finite deformation. Based on this type of element, a bi-linear
shape function is used. All the internal state variables (such as
stresses, plastic work, void ratio, etc.) are updated using the
explicit forward Euler integration scheme. The Newton-
Raphson method is employed to fulfill the static equilibrium
equations. For the quadrilateral 4-noded element:
k
4
k
k=1
i
i
j
j
X
N X
(11)
k
4
k
k=1
i
i
j
j
u
N u
(12)
where,
ξ
i
= material point position at time (
t
) in the local co-
ordinate system;
X
i
= material point position at time (
t
-Δ
t
) in the
global co-ordinate system;
N
= standard bi-linear shape function
for computing strains, positions and etc. at nodal points. In the
global system, for the body with volume (
V
), surface (
S
), total
number of elements (NE) and total number of nodes (NN):
2
1
1
1
1
1
K k
( (
)
CO
n
n
n
T
n
T n
T
n
S
V
V
N M d S I N c d V B md V
1
)
(13)
1
1
1
1
1
1
1
( (
)
n
n
n
T n
n
T n
T
n
S
V
V
N T d S
N b d V B d V
)
K k
(14)
where, K (K = 1, 2, ..., NE) = element number; k (k = 1, …,
4) = node number for a given element;
T
= traction force;
M
=
traction couple stress;
I
= first moment of inertial for the micro-
medium;
ρ
= micro-medium density;
b
= body force per unit
volume;
c
= body couple per unit volume;
B
CO2
= element
matrix; and
B
= strain-nodal displacement matrix. In this sense,
the residual load vector should be vanished to satisfy the below
equilibrium equation:
1
1
(( )
( )
) 0
c T n m
T n
R u R
N
(15)
where,
δω
c
is virtual Cosserat rotation; and
δu
is virtual
displacement.
4 NUMERICAL INVESTIGATIONS OF MICRO-POLAR
EFFECTS WITHIN SHEAR BANDS
For numerical investigations of the evolution of micro-polar
effects in granular materials under shearing, firstly a plane
granular soil layer located between very rough parallel
boundaries is considered. Particularly, a section with the initial
height of
h
0
= 4
cm
and the width of
b
= 10
cm
is discretized by
4-noded elements. Apart from stress and displacement boundary
conditions of non-polar continuum, additional non-standard
micro-polar kinematical boundary conditions, i.e. couple stress
and Cosserat rotation boundary conditions, must also be defined
for the present model. Here, special micro-polar boundary
conditions are introduced across the lateral boundaries of
infinite layer due to the symmetry condition with respect to any
vertical section (Ebrahimian et al. 2012). The top surface of
granular layer is assumed to be fixed not to occur sliding and
rotating. The vertical pressure (
P
0
= 100
kPa
) is kept constant at
the top surface of layer. However, the height of layer can be
changed as the result of dilation or contraction of material under
shearing. Concerning the interaction between granular layer and
bounding structure, it is supposed that the soil grains are
captured by the very rough surface of bounding structure at the
bottom. Furthermore, the vertical displacement is zero (
u
2
= 0)
along the bottom (
x
2
= 0). A quasi-static shear deformation is
initiated through constant horizontal displacement increments,
prescribed at the bottom surface of granular layer. It is assumed
that the granular layer is initially homogeneous and isotropic
(initial void ratio = 0.6). The calibrated material constants for a
dense silica sand given in (Ebrahimian et al. 2012) are used in
following numerical simulations.