526
Proceedings of the 18
th
International Conference on Soil Mechanics and Geotechnical Engineering, Paris 2013
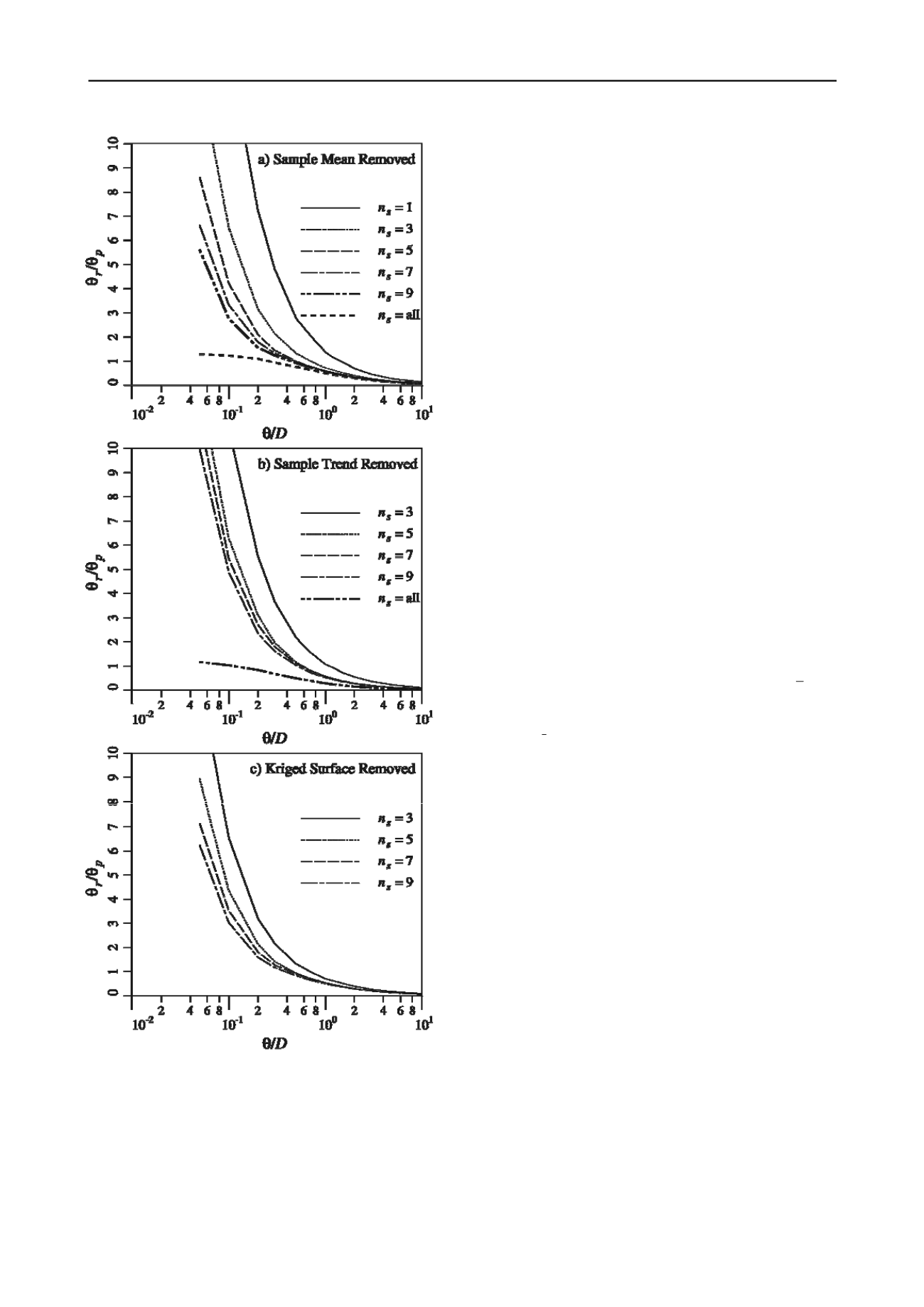
In general, when
D
the estimated correlation length is
overestimated, and often considerably overestimated, especially
when the actual correlation length is small. This occurs because
errors between the estimated trend (of any of the three types)
and actual bilinear field trend (bilinear because correlation is a
measure of the degree of linear dependence between random
variables) are perceived in the estimation process to be caused
by a strong lingering correlation (and not by an error in the
original trend estimate) – hence a longer correlation length is
estimated to account for the evident residual trend.
Of the three trend types considered, the best is the constant
sample mean and the worst is the bilinear trend (except when
s
n
all). The Kriged surface is slightly worse than the constant
sample mean. For example, when
and
9
s
n
/
0.0
D
5
, then
5 6
/
.
r
, 10.0, and 6.3 for the constant sample mean,
bilinear trend, and Kriging surface, respectively. It should be
noted that the best performer, the constant sample mean, may be
so only because the simulated field is assumed stationary (i.e.
constant mean).
At the other end of the plot, where
D
, the correlation
length is underestimated (
1 /
r
). In general, this is because
the removal of a trend in a strongly correlated field is also
removing the evidence of the strong correlation (strong
correlation is evidenced by a trend having little variation off the
trend) resulting in a residual field without strong correlation –
hence a small correlation length. Of the three trend types
considered the best performer at the large correlation length end
is again the constant sample mean. For example, when
9
s
n
and
/
1
D
0
, then
r
/
0.08
, 0.05, and 0.06 for the
constant sample mean, bilinear trend, and Kriging surface,
respectively.
3 CONCLUSIONS
There is no difference between the accuracies of the trend type
selected when matching the trend to the field average,
r
. As
expected, the accuracy improves as the number of samples and
the correlation length increase. If a target standard
deviation,
r
, equal to 20% of the random field standard
deviation,
cell
, is desired, then only one sample is required if
/
D
10
, while 9 or more samples are required if
/
1
D
.
In general, if the correlation length is small, the most
accurate approach is to use a constant sample mean, which
shows the best general results for all three measures of accuracy
considered in this paper. Kriging is almost identical, only losing
out slightly when considering the residual estimated correlation
length. At the other end of the scale, when the correlation length
is large, the bilinear trend is more accurate with respect to the
residual standard deviation than is the constant sample mean, as
expected.
In the absence of knowledge about the actual correlation
length, it appears that the Kriging surface removal, although not
generally the best in any one measure, is very competitive and is
certainly a good overall choice.
4 REFERENCES
Fenton G.A. and Vanmarcke, E.H. 1990. Simulation of Random Fields
via Local Average Subdivision,
ASCE Journal of Engineering
Mechanics
, 116(8), 1733 – 1749.
Figure 3. Estimated correlation length of the residual, normalized by the
point correlation length, versus normalized actual correlation length.
The correlation length estimated from the residual,
r
, will
agree with the actual correlation length used in the simulation,
, when the ratio
r
1 /
. It can be immediately seen in
Figure 3 that this only occurs in general when the entire field is
sampled and the correlation length is relatively small (i.e.
significantly less than
D
). That is, when the entire field is
sampled (
s
all), so that the sample average is equal to the
actual field average, the estimated correlation length becomes
equal to the actual correlation length when the samples are
relatively independent (small
n
).
Heisenberg W. 1927. Über den anschaulichen Inhalt der
quantentheoretischen Kinematik und Mechanik,
Zeitschrift für
Physik
, 43(3-4), 172 – 198.
Lloret-Cabot, M., Hicks, M.A., and Van Den Eijnden, A.P. 2012.
Investigation of the reduction in uncertainty due to soil variability
when conditioning a random field using Kriging,
Géotechnique
Letters,
2, 123 – 127.


