500
Proceedings of the 18
th
International Conference on Soil Mechanics and Geotechnical Engineering, Paris 2013
de vitesse particulaire
v(x,t)
représentées par la superposition
des ondes élémentaires.
2
2
2
2
2
),(
),(
x
txu c
t
txu
t
(1)
) /
(
) /
(
),(
t
r
t
d
cx t u cx t u txu
(2)
) /
(
) /
(
),(
t
r
t
d
cx t
cx t
tx
(3)
) /
(
) /
(
),(
t
r
t
d
cx t v cx t v txv
(4)
Il est possible de montrer que l’expression (4) peut être
exprimée en fonction des ondes de déformation
ε
d
et ε
r
.
) /
(
) /
(
),(
t
r
t
d t
cx t
cx t
c txv
(5)
La connaissance des ondes
ε
d
(t)
et
ε
r
(t)
permet ainsi de
décrire entièrement le phénomène dynamique du battage
pénétromètrique en tout point
x
le long des tiges.
Dans la
pratique, cette connaissance peut se faire à l’aide de mesures
réalisées par le biais de jauges de déformation et/ou
d’accéléromètres. Toutefois, dans les enregistrements réalisés
lors du battage, ces ondes se trouvent souvent imbriquées les
unes avec les autres et il devient nécessaire de les découpler.
2.1
Découplage d’ondes et construction de la courbe charge-
enfoncement en pointe
Différentes méthodes peuvent être employées pour découpler
les ondes
ε
d
(t)
et
ε
r
(t)
à partir des enregistrements réalisés.
Celles-ci diffèrent suivant le type de mesures (déformation,
accélération…), suivant la quantité (
1… n
) ainsi que suivants les
conditions aux limites imposées. Toutefois, il a été montré que
la méthode proposée par (
Casem et al. 2003
) est celle qui
s’adapte le mieux au cas du battage pénétromètrique. A partir
des enregistrements
ε
A
(t)
et
v
A
(t)
réalisés dans un point
A
, les
ondes
ε
d
(t)
et
ε
r
(t)
sont découplées d’après :
t
A
A
r
t
A
A
d
c
t v t
t
et
c
t v t
t
)(
)(
2
1 )(
)(
)(
2
1 )(
(6)
En supposant les efforts externes nuls le long de tiges, la
connaissance de
ε
d
(t)
et
ε
r
(t)
permet de calculer les signaux de
force
F
N
(t)
et de vitesse
v
N
(t)
pour tout point
N
situé en dessous
du point de mesure
A,
notamment dans la pointe,
selon la
solution proposée par (
Karlsson et al. 1989
).
)
(
)
(
2
)
(
)
(
2
1 )(
)1 (
1
)1 (
1
)1 (
1
)1 (
1
n n
N
n n
N
n
n n
N
n n
N
N
t
t
v
t
t
v Z
t
t
F
t
t
F t F
(7)
)
(
)
(
2
1
)
(
)
(
2
1 )(
)1 (
1
)1 (
1
)1 (
1
)1 (
1
n n
N
n n
N
n
n n
N
n n
N
N
t
t
F
t
t
F
Z
t
t
v
t
t
v
t v
(8)
avec
Δt
n-(n-1)
=
(x
n-1
-x
n
)/c
n
et
Z
n
=E
n
A
n
/c
n
l’impédance mécanique
de la section
n
définie par son module de Young
E
n
, sa section
A
n
et la célérité de l’onde
c
n
. Ainsi, à partir des enregistrements
ε
A
(t)
et
a
A
(t)
il est possible de calculer les signaux de force
F
p
(t)
,
vitesse
v
p
(t)
et enfoncement
s
p
(t)
en pointe et donc de tracer la
courbe
p
-s
p
pour chaque coup de marteau fourni lors du
battage. De nombreux tests ont été réalisés pour valider la
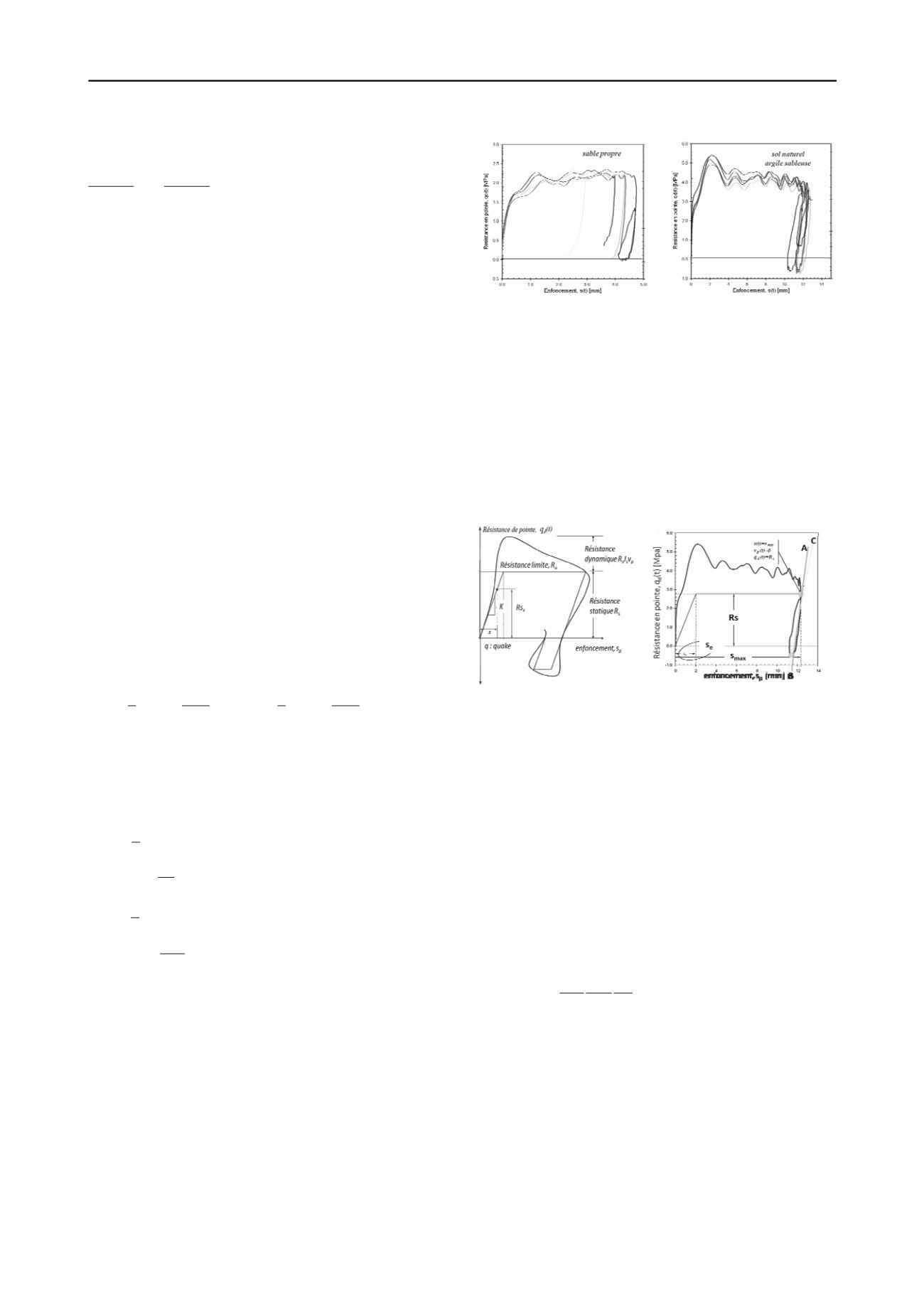
faisabilité d’un tel essai. Dans la
figure 2
on présente un
exemple de courbes obtenues pour deux types de sol. On peut
remarquer que ces courbes sont répétitives pour un même
matériau et varient selon la nature du milieu ausculté permettant
d’identifier des comportements différents.
2.2
Exploitation de la courbe charge-enfoncement
p
-s
p
Pour interpréter la courbe
p
-s
p
il a été proposé une
méthodologie fondée sur les travaux de (
Smith 1962
).
Figure 2. Exemple de courbes charge-enfoncement pénétromètriques
obtenues avec le Panda 3 pour deux types de sol (c.f. Benz 2009).
Pour chaque impact, on calcule des paramètres de résistance,
d’amortissement, de déformation ainsi que de célérité d’ondes
dans le sol.
2.2.1
Paramètres de résistance
En supposant que la contrainte en pointe
qd(t)
est la
résultante des composantes statiques
R
s
(obéissant à une loi
élastoplastique parfaite) et dynamiques
R
d
(t)
(proportionnelle à
la vitesse d’enfoncement
v
p
(t)
); on détermine la valeur de
R
s
en
admettant que lorsque
v
p
(t)
est nulle la composante dynamique
R
d
(t)
s’annule et
R
s
est donc égale à
qd(t).
Figure 3. (a) Modèle de Smith et (b) exploitation de la courbe
p
-s
p
Les valeurs de
R
d
(t)
et du coefficient d’amortissement de
Smith
J
s
sont déterminés dans l’intervalle d’enfoncement [
s
e
;
s
max
], avec
s
e
et
s
max
les enfoncements élastique et maximal, en
écrivant que
R
d
(t) = q
d
(t)-R
s
et
J
s
=R
d
(t)/(R
s
v
p
(t))(
figure 3.b).
2.2.2
Paramètres de déformation
Une fois l’enfoncement maximal
s
max
atteint, on admet que
sol et pénétromètre se mettent à vibrer ensemble dans un régime
pseudo-élastique. Dans cette partie de la courbe
p
-s
p
, deux
modules sont ainsi définis : un module de déchargement
E
d
P3
(droite
AB
) et un module de rechargement
E
r
P3
(droite
BC
)
(figure 3.b). En assimilant la pointe à une petite plaque
encastrée à l’intérieur d’un massif élastique semi-infini, on
calcule la valeur de
E
d,r
p3
en appliquant la équation de
Boussinesq (9) proposée par (
Arbaoui 2006
).
M
p
p
d
rd
p
k
d
s
q
E
1
4
)
1(
2
'
3
(9)
avec
ν
supposé égal à 0,33,
d
p
le diamètre de la pointe et
k
M
le
coefficient d’encastrement de mindlin.
2.2.3
Célérité des ondes c
p
et c
s
La célérité des ondes de compression
c
p
et de cisaillement
c
s
dans le sol est calculée par le biais des polaires de choc
préconisée par (
Aussedat 1970
). Pour chaque impact on mesure
les pics des ondes descendantes et remontantes dans un espace
de temps
to+2L
t
/c
t
nous permettant de calculer la valeur de
c
p
(Benz 2009). La valeur de
c
s
est calculée d’après l’expression
(10) en supposant la valeur de
ν
égale à 0,33.


