466
Proceedings of the 18
th
International Conference on Soil Mechanics and Geotechnical Engineering, Paris 2013
e
f
p
p
(
3
)
Both
f
and
f
are functions of ice ratio
e
i
. Soils become
stronger upon freezing, which is characterized by higher
preconsolidation stress
p
o
, and the slopes NCL and URL lines
become flatter (Qi
et al.
, 2010). A reasonable relative position
of normal compression lines for a soil in both unfrozen state and
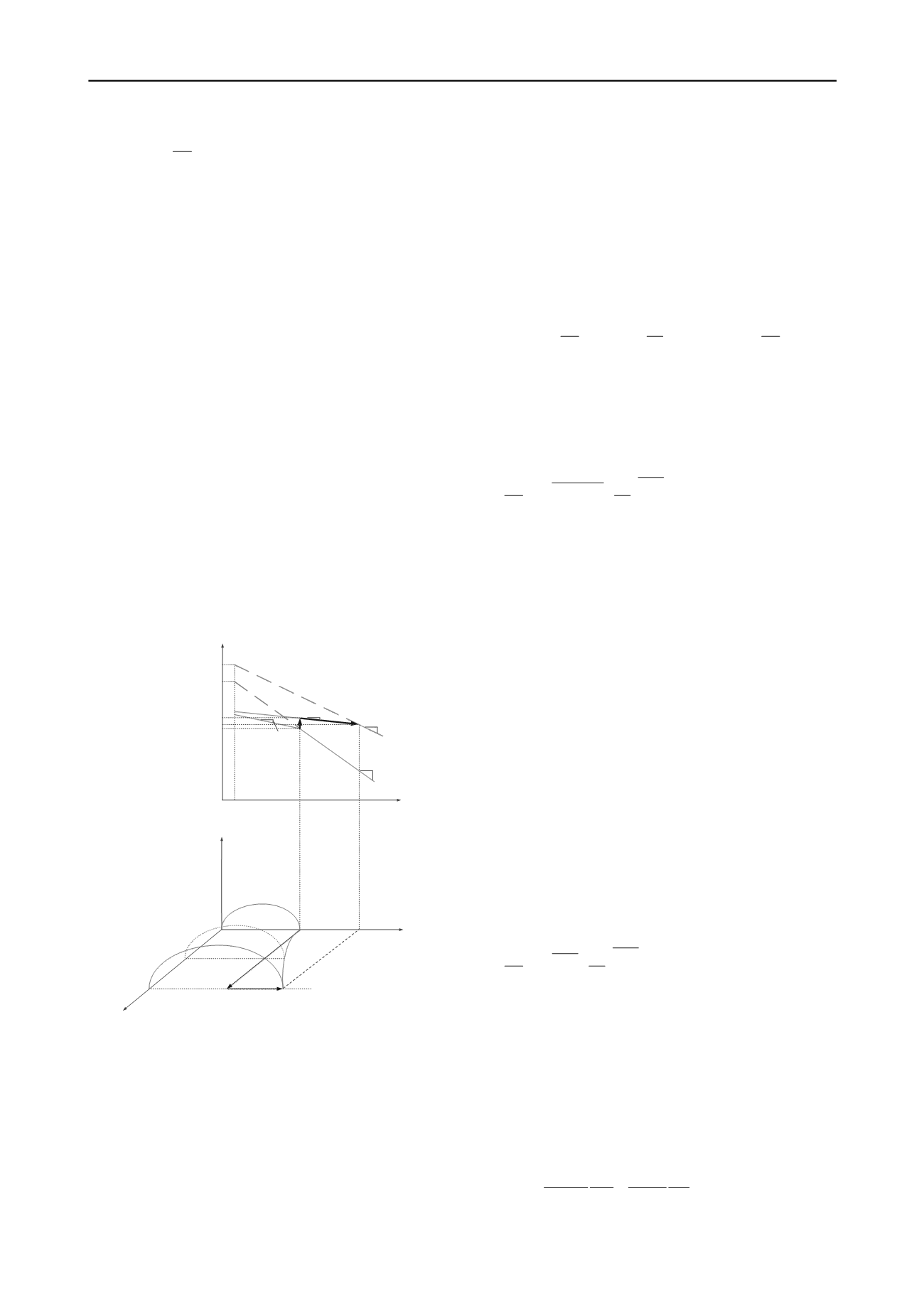
frozen state is shown in Figure 1(a). The relationship between
preconsolidation stress and ice ratio is illustrated in Figure 1(b).
The yield surface has elliptical shape in
q,p
-plane (deviatoric,
isotropic stress), and its evolution, as function of
e
i
, is illustrated
in Figure 1(b).
p
o
is the preconsolidation stress for unfrozen
soil, and
0
f
p
is the preconsolidation stress for the same soil in
frozen state with the ice ratio of
(
i
i
e e
C
0
r
p
is the reference
stress).
Consider freezing and loading path B-C-D as illustrated in
Figure 1a. A virgin compressed unfrozen soil (saturated) at
point B is subjected to freezing under a constant isotropic stress
state. The specific volume increases due to the volumetric
expansion upon phase change. Then, isotropic load is added at
constant temperature until point D is reached on the isotropic
stress yield line for the frozen soil. During the isotropic loading
process the ice ratio remains constant,
. This is because
the ice ratio follows the unfrozen water content curve in non-
segregation freezing process, thus having a unique relationship
to the temperature. The unfrozen water content will be
discussed in the next section.
i
iC
e e
q
i
e
B
C
D
O
iC
e
ln
p
0
p
0
f
p
( )
a
( )
b
ln
p
0
p
0
f
p
B
C
D
0
r
p
0
0
f
B
f
f
C
D
Figure 1 (a) freeze-thaw thermal loading path in v-ln(p) plane;
(b)“pseudo preconsolidation pressure” changing along BD due to
increasing pore ice ratio
Points B and D belong to the same yield curve on
p
, –
plane, and yield stresses
i
e
0
f
p
for frozen states with different ice
ratio during freezing from point B to C are located on curve
BD (Figure 1(b)).
i
e
The specific volume at the final point D can be described as
D B
BC
C
where
v
BC
and
v
CD
are the increments due to initial freezing
and due to subsequent loading.
The expansion upon freezing is related to phase change and
is treated as reversible, because it reversed during thawing. This
volume change can then be calculated as
0.09
f
i
e
(
5
)
Substituting equations (2), (
3
), and (5) into (4) renders the
following equation
0
0
0
0
0
0
ln
(
ln ) 0.09
ln
0
0
f
f
f
f
i
r
r
p
p
e
p
p
f
p
p
(
6
)
where
0
r
p
is the reference pressure to locate the virgin
compression lines for both soil states. Consequently, the
increase in isotropic yield stress caused by the ice ratio increase
is found as
0 0
0.09
0
0
0
0
f
f
i
f
f
f
f
e
f
r
r
p
p
e
p
p
(7)
The slopes of the NCL and URL of frozen soil are both
functions of . This path of derivation was followed earlier by
Alonso
et al
. (1990) in the context of unsaturated soils.
Because the frozen soil has limited tendency for compression
(pores are filled with ice), slopes
i
e
f
and
f
drop dramatically
compared to those for the unfrozen soil. The following
relationships are postulated
1
exp(
)
f
i
e
(
8
)
2
exp(
)
f
i
e
(
9
)
where
1
and
2
are soil constants.
In order for equation (7) to yield
p
0
for unfrozen soil when
e
i
= 0, we postulate the following linear law defining the shift of
v
0
to
v
f
as function of
e
i
0
0
( 0.09 )
f
i
e
(
10
)
where
β
is a soil constant. Equation (7) can, therefore, be
written as
0
0
0
0
f
i
f
f
f
f
e
f
r
r
p
p
e
p
p
(
11
)
An illustration of how the preconsolidation stress
0
f
p
changes in soil with progressively increasing ice ratio
e
i
is
shown in Figure 2, for three cases, each starting from a different
preconsolidation stress
p
0
for unfrozen soil (the following
parameters
were
used:
,
1
2
0.2
0
,
0.35
,
0.07
)
The plastic volumetric strain due to mechanical load and
thermal process can be calculated as
0
0
0
0
f
f
f
f
pl
v
f
dp
dp
d
v p
v p
(
12
)
D
(
4
)


