459
Technical Committee 101 - Session II /
Comité technique 101 - Session II
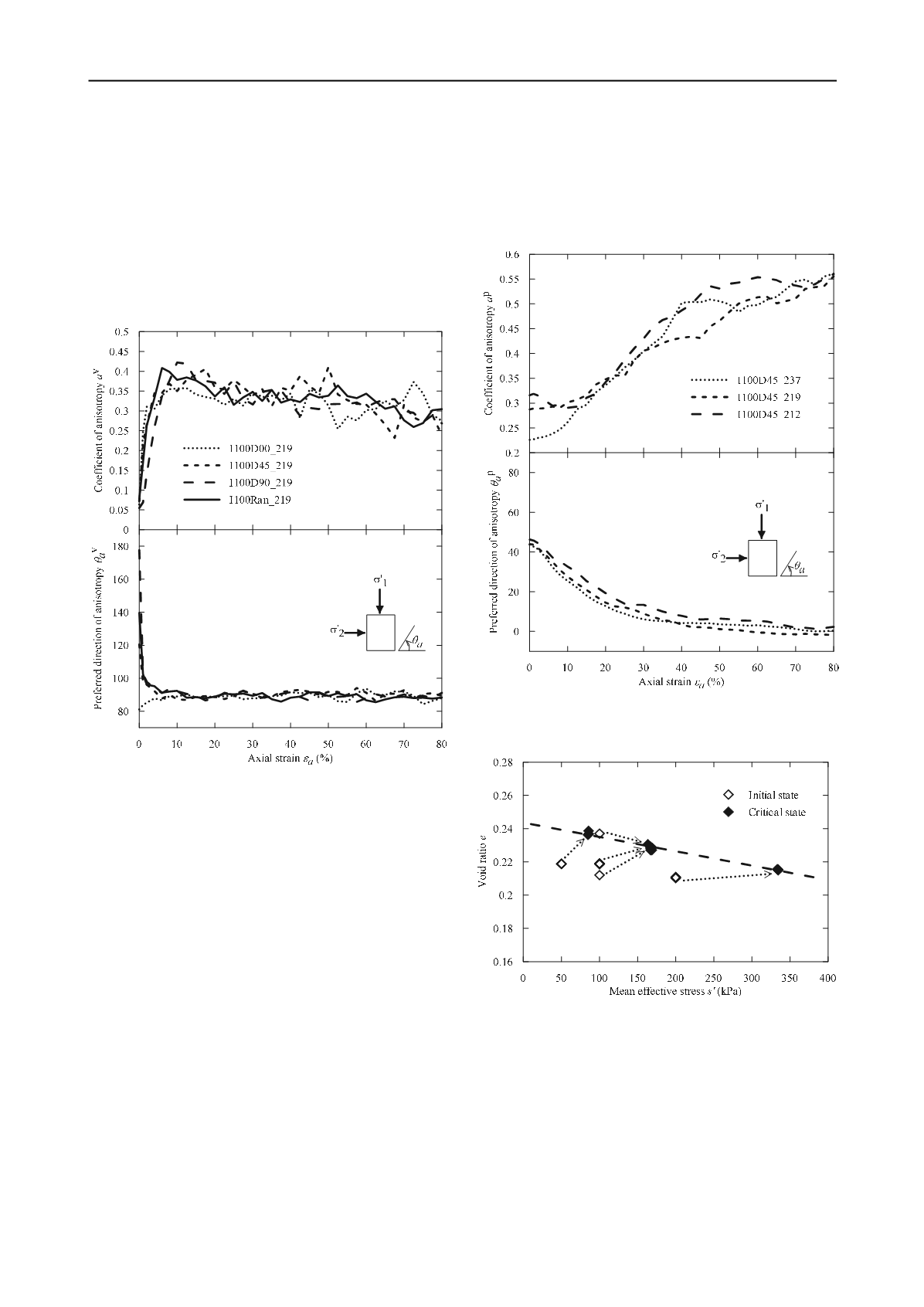
A void space is defined following Li and Li (2009). Figure
3 shows its evolution with shear. It can be seen from the figure
that the void space evolutes from a highly isotropic distribution
prior to shear commencement to an anisotropic one at large
strains with a preferential orientation in the direction of the
major principal stress (
v
90
a
). Substantial amount of
anisotropy is developed within 10% axial strain. Initial fabric
seems to have very little influence on the evolution of void
fabric. Like particle orientation, a unique void fabric is
exhibited at large strain (
v
0.3
a
and
v
90
a
).
Figure 3. Evolution of void space fabric
–
the influence of initial
fabric.
4.2
Influence of initial density
Figure 4 shows the effect of initial density on the evolution of
particle orientation fabric. Deposited assemblages (D45)
confined at 100 kPa having three different initial densities
(initial void ratio from loose to dense = 0.237, 0.219 and 0.212,
respectively) are investigated. Firstly, the particle orientation
fabric changes gradually with increasing axial strain. The
coefficient of anisotropy
p
a
increases gradually with axial
strain while
p
changes from its initial value (45°) to 0°. It
means that the particles align with their long axis perpendicular
to the loading direction when subject to prolonged shearing. A
noticeably anisotropic and unique fabric can be observed at
large strains. The effect of initial density is minimal. The
evolution of void space fabric exhibits very similar behavior as
the one shown in Figure 3, regardless the initial density of the
assemblage.
4.3
Critical state
Figure 5 shows the initial and critical state of the assemblages in
an
e
-
s
’ space where
1
2
'
'
'
/ 2
s
. Initial state of the
specimen includes various void ratios and fabrics confined at
different pressures. It can be seen that a unique line can be used
to describe the critical state. Together with the findings as
revealed from Figure 2-4, it is known that a critical state can be
achieved at very large strains where not only the density and
mean stress reaches a steady value but also a unique fabric is
obtained. Furthermore, the fabric at critical state is correlated to
the loading direction. The results echo the theory proposed by
Li and Dafalias (2012).
Figure 4. Evolution of particle orientation fabric
–
the influence of
initial density.
Figure 5. Initial and critical states of the study assemblages.
4.4
Limitations
The findings of unique fabric at critical state are obtained by
conducting numerical tests limited to monotonic biaxial
shearing of specimens composed of idealized mono-sized pill
shape particles. Tests with continued changing of loading
direction are not considered herein.
5 CONCLUSIONS
A series of numerical biaxial compression tests is undertaken on
idealized two-dimensional granular specimen having various


