143
Honour Lectures /
Conférences honorifiques
17
depth is identical to that for the case of consolidation,
where
H
d
is the maximum drainage distance, whereas the
definition for the diffusive time factor,
T
*
, is identical to
that for the dimensional consolidation time factor,
T
, where
D
a
is replaced by the coefficient of consolidation,
c
v
(Shackelford and Lee 2005). On the basis that pumping
results in "instantaneous" removal of contaminant from the
surrounding aquifer at time
t
=
T
*
= 0, the resulting
contaminant concentration profiles for
T
*
> 0 can be
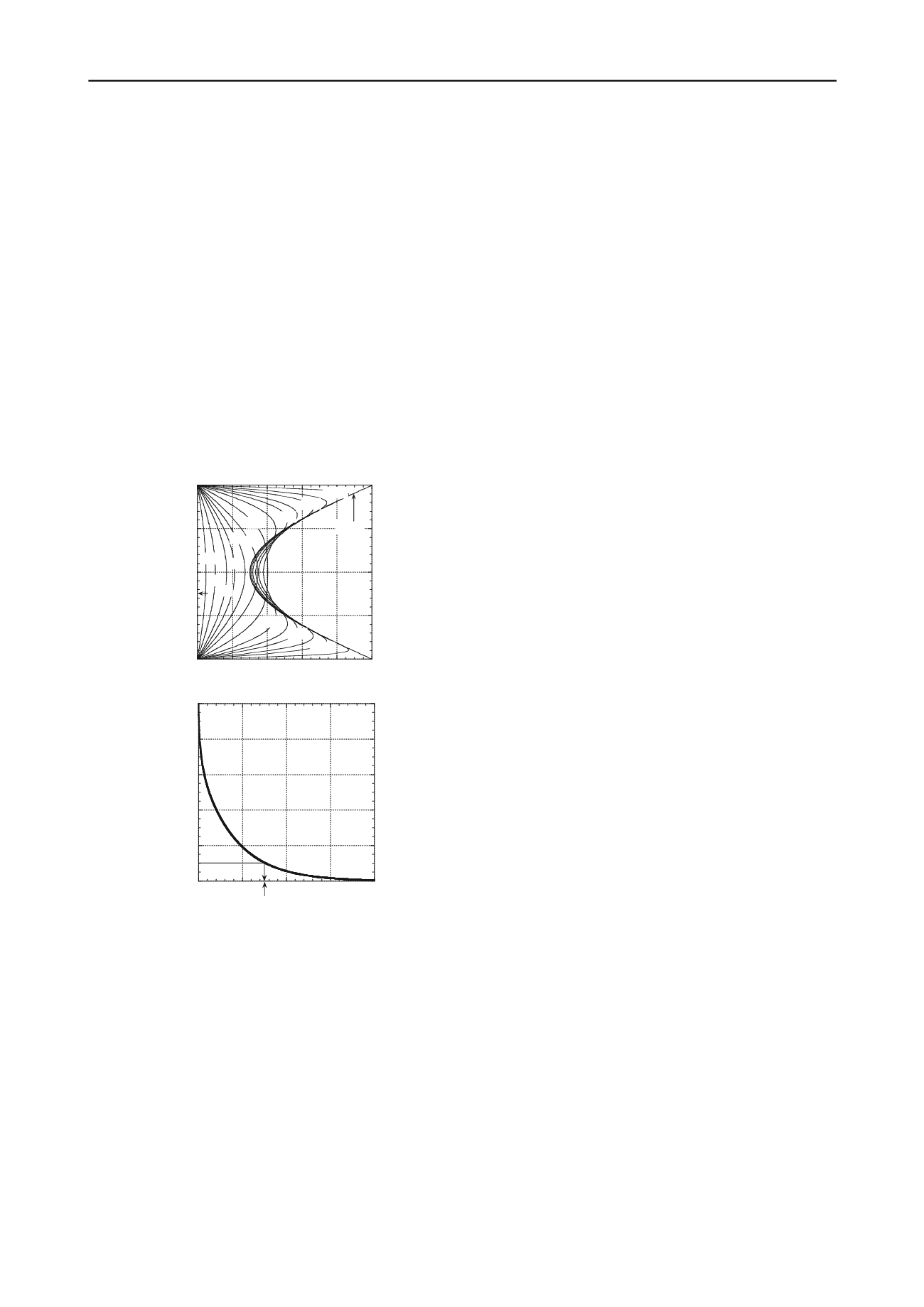
determined by means of superposition as shown in Fig.
22a. At times,
T
*
, less than about 0.1, both outward
diffusion at the boundaries and inward diffusion near the
center of the clay lens are occurring simultaneously,
whereas after
T
*
0.1, the concentration profiles have
dissipated to the extent that only outward diffusion of TCE
occurs. The dissipation of residual contamination will
proceed over time until all of the contaminant initially
within the clay lens has diffused into the surrounding
aquifer and been removed. However, this mass removal
can take considerable time.
0 0.2 0.4 0.6 0.8 1
0
0.5
1
1.5
2
(a)
Relative Solute Concentration,
C
(
Z
,
T
*
)/
C
o
Dimensionless Depth,
Z
=
z
/
H
T
*
= 0
0.001
0.05
0.03
0.01
0.02
0.1
0.2 0.3
0.4
0.5
1.0
0.7
0.005
0
20
40
60
80
100
0
0.5
1
1.5
2
(b)
Average Degree of Diffusion,
U
*
(%)
Dimensionless Diffusive Time Factor,
T
*
T*
~ 0.76
Figure 22. Results of example analysis for the reverse matrix
diffusion from 1-m-thick clay lens contaminated with TCE
resulting in an initial sinusoidal contaminant distribution: (a) time-
dependency of relative TCE concentration versus dimensionless
depth; (b) time dependency of the average degree of diffusion for
contaminant removal (modified after Shackelford and Lee 2005).
For example, if we assume an
R
d
of 5.2 and
D
*
of 3.33
x 10
-10
m
2
/s for TCE and the clay based on Parker et al.
(1996), then the degree of diffusion,
U
*
, which represents
the relative degree of mass removal (Shackelford and Lee
2005), 10 yr after the beginning of pumping (i.e.,
T
*
~
0.081) is approximately 0.43 or 43 %. Based on a porosity,
n
, of 0.60 for the clay lens and assuming complete
reversibility of the sorbed TCE, the cumulative
contaminant mass removed per unit area of the clay lens
after 10 yr of pumping is approximately 749 g/m
2
(Shackelford and Lee 2005). More importantly, as
indicated in Fig. 22b, 90 % contaminant mass removal
(i.e.,
U
*
= 0.90) corresponds to
T
*
of approximately 0.76,
which is equivalent to 95 yr. Thus, this analysis indicates
that approximately a century of pumping would be
required to remove 90 % of the initial contaminant mass
from a partially contaminated, 1-m-thick clay lens, which
is consistent with the aforementioned observations
attributing failure of some pump-and-treat systems to
reverse matrix diffusion.
A similar analysis was presented by Feenstra et al
(1996), but they assumed that the clay lens was initially
completely (i.e., uniformly) contaminated. Such complete
contamination of non-fissured clay lenses via matrix
diffusion would be likely only in the case of relatively thin
clay lenses and/or relatively long durations of aquifer
contamination. Otherwise, the clay lenses likely would
only be partially contaminated resulting in an initial
concentration distribution within the clay lenses that is
sinusoidal, thereby requiring the need for superposition in
the resulting analysis (Shackelford and Lee 2005).
Regardless of the level of contamination or the type of
analysis required, this example supports the numerous
observations that reverse matrix or back diffusion can play
a significant role in affecting the remediation of
contaminated aquifers.
5.2
Diffusion through Subaqueous Caps for
Contaminated Sediments
Contaminated, subaqueous sediments represent a major
environmental issue worldwide. One approach for dealing
with this issue is to cap the sediments in situ. The caps
should perform one or more of the following functions
(Alshawabkeh et al. 2005): (a) physical isolation of the
sediment; (b) sediment stabilization, in terms of preventing
erosion and resuspension; and (c) reduction of dissolved
contaminant flux. A conceptual schematic of the role of
capping in situ sediments is illustrated in Fig. 23.
Placement of the capping layer will reduce contaminant
flux by (1) eliminating the bioturbation zone (i.e., mixing
or dispersion caused by benthic organisms at the top
several centimeters of the contaminated sediments), (2)
increasing the length through which contaminants must
migrate via advection and diffusion, (3) retarding
contaminant migration via sorption to the capping
materials, and (4) eliminating resuspension and direct
desorption of contaminants to the overlying water column
(Wang et al. 1991, Thoma et al. 1993). Capping materials
do not necessarily have to be low permeability soils, as
typically is the case with covers for above ground waste
disposal, but the materials should possess some sorption
capacity to minimize the rate of contaminant migration
through the cap.
Initially, contaminant migration through the cap will
occur both via advection and diffusion. The advective
component of contaminant transport results from
generation of excess pore-water pressures within the
contaminated sediments due to placement of the capping
material and the associated sediment consolidation. Some
studies have indicated that consolidation induced
contaminant mass flux can be several times greater than
that due to diffusion during the initial, transient period
when consolidation of the sediments is pronounced (e.g.,
Alshawabkeh et al. 2005). Nonetheless, diffusion still may
play a significant role in terms of the contaminant mass
flux through the cap during the initial transient transport
stage of the process, and likely will be the dominant
transport process under long-term, steady-state conditions


