141
Honour Lectures /
Conférences honorifiques
15
repositories (Conca and Wright 1990), and unsaturated
diffusion of chemicals in the vadose zone (Charbeneau and
Daniel 1993).
As an example of this last scenario, Rowe and Badv
(1996b) evaluated the diffusion of chloride and sodium
through a layered soil system consisting of an essentially
saturated clayey silt overlying an unsaturated layer of
either coarse sand or fine gravel. This two-layered soil
system mimics the practical situation where a landfill may
be sited in a hydrogeological setting where the
predominant soil type below the proposed landfill base is
granular (e.g., silt, sand, or gravel) and the water table is
also at some depth. In this case,
S
w
of the soil below a liner
may be expected to increase from about residual
w
below
the liner to almost full saturation (
S
w
= 1) at or near the
water table. Based on the results of their study, Rowe and
Badv (1996b) found that the value of
D
*
for chloride and
sodium in the unsaturated soil, or
D
*
unsat
, relative to that in
the saturated soil,
D
*
sat
, could be approximated reasonably
well by a simple linear function of
w
, or
D
*
unsat
/
D
*
sat
=
w
/
n
. Also, Rowe and Badv (1996b) concluded that,
provided that the Darcy velocity can be kept low (e.g., by
the construction of a good compacted clay or composite
liner), the unsaturated fine gravel evaluated in their study
may act as a diffusion barrier to the migration of the
dissolved sodium and chloride ions.
4.5
Gas-Phase Diffusion
Gas-phase diffusion can be an important consideration in
environmental geotechnics,
including both waste
containment applications (e.g., Yanful 1993, Aubertin et
al. 2000, Mbonimpa et al. 2003, Aachib et al. 2004,
Bouzza and Rahman 2004, 2007, Alonso et al. 2006,
Demers et al. 2009) and remediation applications, such as
in the use of the soil vapor extraction technology for
removal of VOCs from the subsurface vadose zone (e.g.,
Johnson et al. 1990). The importance of gas-phase
diffusion is accentuated because diffusion coefficients for
chemicals in the gas-phase typically are four-to-five orders
of magnitude greater than those for the same chemicals in
the liquid phase (Cussler 1997). For this reason, the gas-
phase diffusive mass flux of a chemical through soil can be
reduced significantly by minimizing the continuity in the
gas (air) phase of the medium, for example, by filling the
voids with a sufficient amount of water such that the gas
phase becomes discontinuous (e.g., Nicholson et al. 1989,
Yanful 1993, Bouzza and Rahman 2004, 2007).
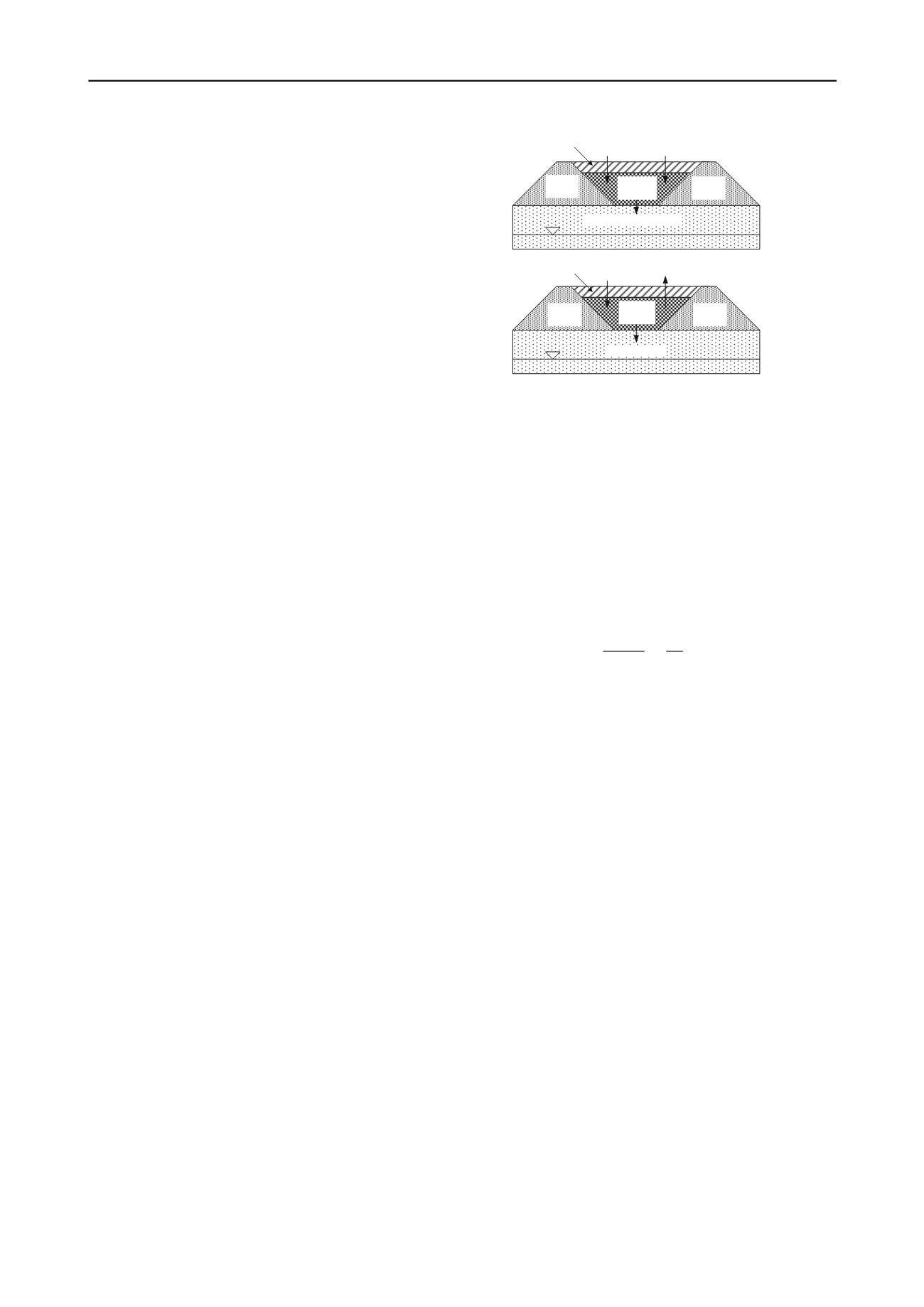
Two waste containment problems of interest involving
gas-phase diffusion and the environmentally safe disposal
of mine tailings are illustrated schematically in Fig. 19.
The problem of acid drainage (Fig. 19a) occurs when
sulphidic tailings (e.g., pyrite or FeS
2
) are oxidized
resulting in the production of a low pH solution (e.g., pH
≈
2) that leaches potentially toxic heavy metals associated
with the tailings during percolation through the tailings,
resulting in the emanation of acid drainage form the
tailings (e.g., Nicholson et al. 1989, Evangelou and Zhang
1995, Ribet et al. 1995). In the case of the disposal of
uranium tailings (Fig. 19b), the tailings can serve as a
localized source of radon gas that can be environmentally
harmful if not controlled properly. In both of these cases,
the objective in the cover design must include steps taken
to minimize diffusive influx (O
2
) or diffusive efflux
(radon) of gas through the cover.
Tailings
Dam
Tailings
Dam
H
2
O
O
2
Acid Drainage (pH < 2)
(a)
Cover
Sulphidic
Tailings
Tailings
Dam
Tailings
Dam
H
2
O Radon
Radionulcides
(b)
Cover
Uranium
Tailings
Figure 19. Tailings disposal scenarios where gas-phase diffusion
plays an important role: (a) oxidation of sulphidic tailings and
generation of acid drainage; (b) radon gas emission (modified
after Shackelford and Nelson 1996, Shackelford 1997).
For example, Stormont et al. (1996) evaluated the effect
of unsaturated flow through the three cover sections shown
in Fig. 20a in terms of the effective air-phase diffusion
coefficient for oxygen gas (O
2(g)
),
D
e
, at a depth of 0.6 m
(i.e., the interface between the cover and the underlying
material). Their results are shown in Fig. 20b in the form
of a normalized oxygen diffusion coefficient,
D
N
, defined
as follows (e.g., see Charbeneau and Daniel 1993,
Stormont et al. 1996):
10/3
e
a
N
e,max
D D
D
n
(7)
where
D
e
is the effective air-phase diffusion coefficient (=
a
a
D
a
),
a
is the volumetric air content,
n
is total soil
porosity,
a
is the apparent tortuosity factor for the air
phase (=
a
7/3
/
n
2
),
D
a
is the pure air-phase diffusion
coefficient (
2.26 x 10
-5
m
2
/s), and
D
e,max
=
D
e
at
a
=
n
.
Thus, 0
≤
D
N
≤ 1, such
that diffusion of O
2(g)
via the air
phase will be minimized as
a
approaches zero (
a
→ 0).
However, as shown by Aachib et al. (2004), minimizing
the diffusion of O
2(g)
via the air-phase does not necessarily
mean that the liquid-phase diffusion of O
2(g)
also will be
unimportant.
As shown in Fig. 20b,
D
N
for the monolithic and
resistive covers remained relatively high because the water
content at the 0.6-m depth tended to remain relatively
constant at the field capacity of the soils. However, in the
case of the capillary barrier,
D
N
was significantly lower
and more variable than the other cover sections, because
the water content immediately above the interface between
the finer and coarser layers remained high due to the
capillary barrier effect. Stormont et al. (1996) attributed
the variability in
D
N
to the variability in water contents
associated with wet and dry seasons.


