2459
Technical Committee 211 /
Comité technique 211
Proceedings of the 18
th
International Conference on Soil Mechanics and Geotechnical Engineering, Paris 2013
sults of the
chemical stabilization of the soft soil of “Baixo Mondego”.
M OTHER CEMENT BASED STABILIZED
ethod here proposed is
versatile as it is valid for other soft soils.
bilization of other 7 soft soils (Horpibulsuk 2001, Kawasaki
et al 1981)
Soft soil
In order to validate this simple method, it will be applied to
other soft soils as presented in the next section.
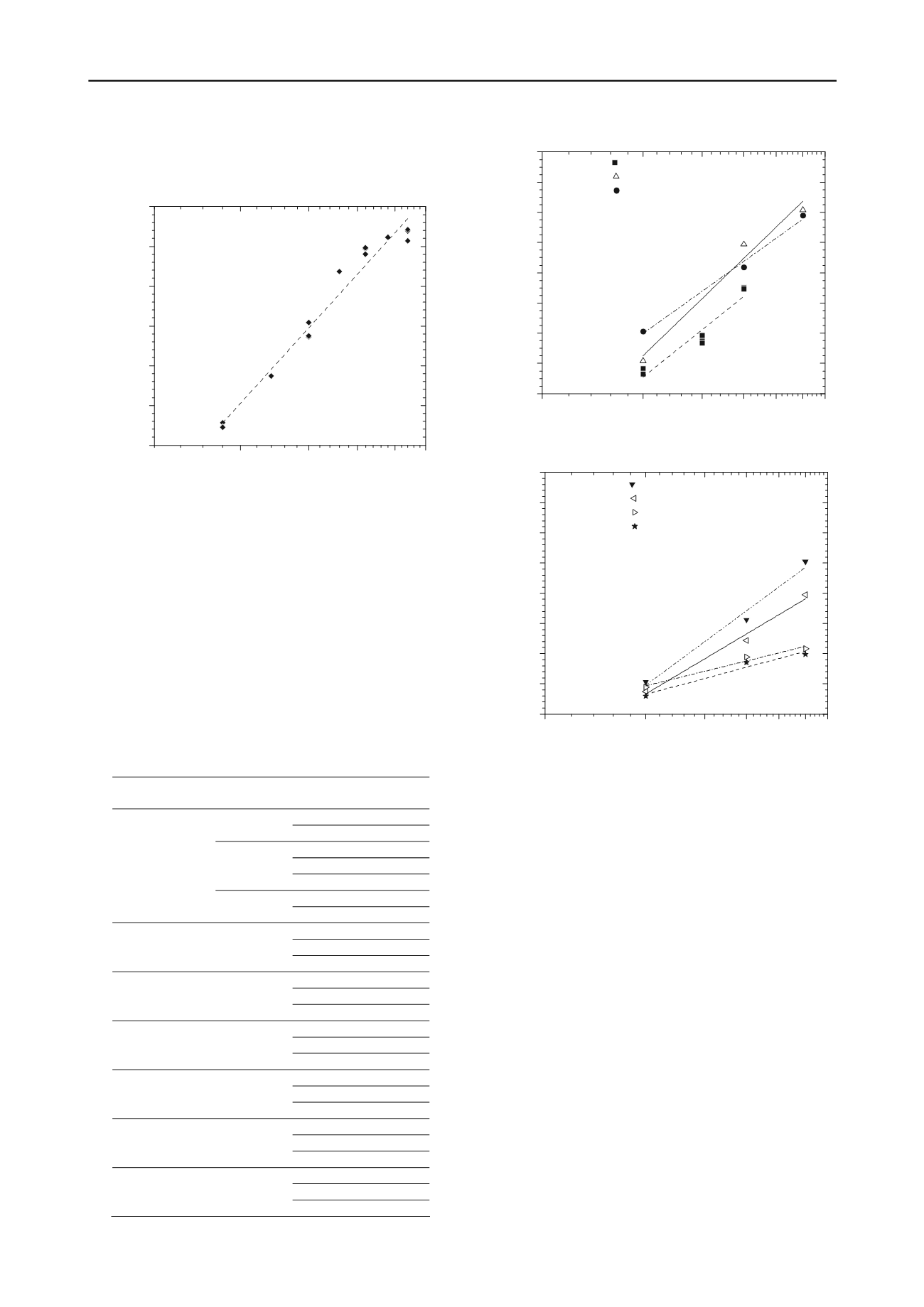
Figure 2. Normalized unconfined compressive strength re
3 DATA FRO
SOFT SOILS
Table 4 presents the main results of 7 other cement based
stabilized soft soils whose geotechnical properties are described
in Horpibulsuk (2001) and Kawasaki et al (1981). Figure 3
presents the results of the unconfined compressive strength
normalized by the liquidity index, from which it can be
concluded that each cement based stabilized soft soil has its
normalization (fitting curve). Thus the m
Table 4. Unconfined compressive strength results of cement based
chemical sta
.
I
L
a
w
q
u max
(-)
(%)
(kPa)
Ariake clay
1.0
10
833
15
1798
1.5
10
434
15
1286
20
2343
2.0
15
839
20
1736
Toky clay
1.
o
0
10
1085
20
4941
30
6072
Chiba clay
1.0
10
2063
20
4189
30
5894
Kangawa clay
1.0
10
1068
20
3120
30
5047
Aichi clay
1.0
10
887
20
1889
30
2159
Osaka clay
1.0
10
595
20
1707
30
1976
Hiroshima clay
1.0
10
748
20
2436
30
3952
5
10
15 20 25
0
1000
2000
Figure 3. Normalized unconfined compressive strength for other cement
based stabilized soft soils.
4 GENERALIZING THE PROPOSED METHOD
As it was observed in Figures 2 and 3, the method proposed can
be applied satisfactory to a wide range of soft soils. However,
each cement based stabilized soft soil has its own fitting
parameters (see the equations for q
IL
in Figures 2 and 3),
different for each soil.
In order to find a generalized strength equation, independent
of the soft soil, the q
IL
data of a particular soft soil was
normalized by the unconfined compressive strength defined for
a liquidity index of 1.0 and for a constant binder content (it was
considered the value 18% for all soft soils), q
IL=1 (aw=18%)
. For
each soft soil, this last value was evaluated from the fitting
curves presented in Figures 2 and 3. All data are presented in
igure 4, where it can be seen that the values are in a narrow
linear band, fitted relatively well by a linear logarithmical
regression (R
2
= 0.94). Thus, the method proposed in this paper
seems to be independent of the soft soil type, being valid for the
prediction of the unconfined compressive strength at 28 days of
curing time of cement based stabilized soft soils, which is
helpful for the laboratory optimization process of the chemical
stabilization. The number of unconfined compression tests
required can be reduced to one if it is applied the generalized
equation and the binder content chosen is 18%.
30 35
3000
4000
5000
6000
700
8000
F
0
A ake clay
ri
Tokyo clay
ay
C ba cl
hi
q
IL
41.90.ln(a
w
932.30 (
q
IL
49.59.ln(a
w
50.40 (R 95)
q
IL
3855.12.ln(a
w
27.90 (
IL
(kPa)
a
w
(%)
2000
4000
5000
6000
7000
8000
34
= 46
=
) - 5
R = 0.98)
2
2
= 0.
) - 94
=
) - 83
R
2
= 0.91)
0
500
1000
1500
2000
2500
3000
10
15
20 25 30
q
IL
= q
u max
x I
L
(kPa)
q
IL
= 2337.63.ln(a
w
) - 4854.76
(R
2
= 0.97)
a
w
(%)
q
5
10
15 20 25 30 35
0
1000
3000
Kangawa clay
Hiroshima clay
Aichi clay
Osaka clay
q
IL
= 1294.43.ln(a
w
) -2327.64 (R
2
= 0.93)
q
IL
= 1188.81.ln(a
w
) -1802.35 (R
2
= 0.94)
q
IL
= 2864.59.ln(a
w
) -5928.20 (R
2
= 0.97)
q
IL
= 3550.61.ln(a
w
) -7217.88 (R
2
= 0.96)
(kPa)
q
IL
a
w
(%)


