2464
Proceedings of the 18
th
International Conference on Soil Mechanics and Geotechnical Engineering, Paris 2013
4.3
Résultats
4
MODÉLE SEMI-ANALYTIQUE SIMPLIFIE
4.1
Principe du modèle
On utilise à présent un modèle semi-analytique simplifié basé
sur la méthode dite « t-z » : la colonne est assimilée à une
poutre verticale travaillant en compression axiale, tandis que le
frottement latéral
τ
et la contrainte en pointe
q
suivent une loi de
mobilisation de Frank et Zhao (1982), et sont donc fonctions du
déplacement vertical de la colonne
w
. Chaque loi est
caractérisée à l’aide de deux paramètres : un paramètre de pente
(
K
t
ou
K
p
) et une contrainte unitaire limite (
q
s
ou
q
p
). Ces lois
sont couramment utilisées en France pour estimer le tassement
d’un élément de fondation profonde, et se révèlent très efficaces
dans les exercices de calage par rapport à un essai de
chargement en vraie grandeur.
Frottement latéral
Contrainte en pointe
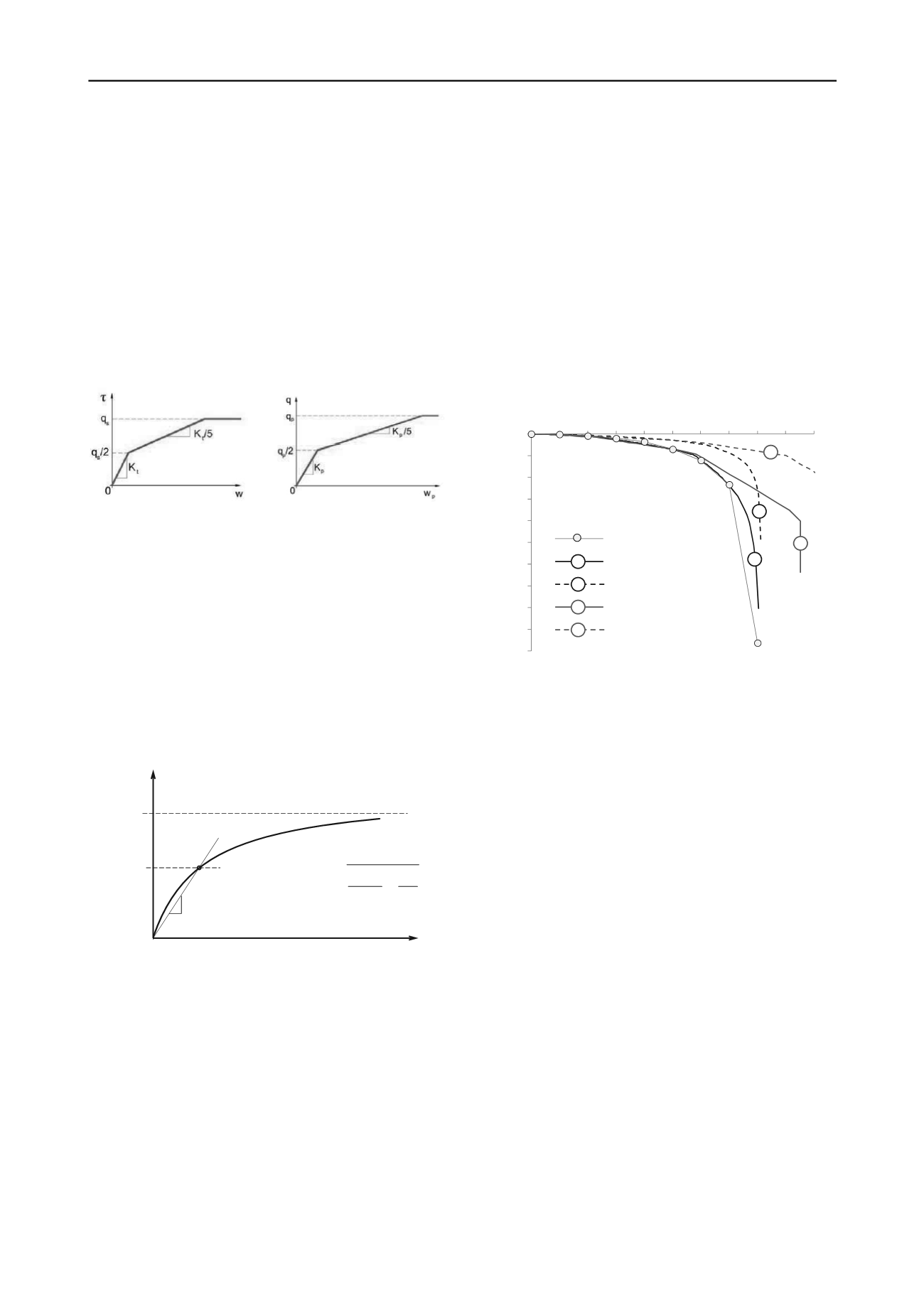
La Figure 11 présente les résultats obtenus (courbe de
chargement). Deux cas ont été étudiés : cas d’un comportement
linéaire élastique de la colonne (E = E
50
), et cas d’un
comportement non linéaire (E = f(σ)) selon la loi décrite dans la
Figure 10. Pour chaque cas, deux situations sont examinées :
frottement de type sol/sol (q
s
= f(σ
v
’)) et frottement de type
béton/sol (q
s
= f(pl*)). Les résultats obtenus confirment la
pertinence d’une loi de comportement non linéaire pour le
matériau constitutif de la colonne, et montrent que le choix d’un
frottement de type « sol/sol » est plus représentatif du
comportement réel observé. Avec ces hypothèses, le résultat du
modèle semi-analytique se révèle très concordant avec celui de
l’essai de chargement jusqu’au palier de rupture. Celui-ci est
obtenu par plastification en tête de la colonne (contrainte
appliquée proche de la résistance à la compression simple Rc).
0
5
10
15
20
25
30
35
40
45
50
0 50 100 150 200 250 300 350 400 450 500
Tassement (mm)
Charge en tête (kN)
1
4
Figure 9. Lois de mobilisation de type Frank et Zhao
2
Les courbes de mobilisation ci-dessus sont combinées avec
la loi de comportement de la colonne, qui relie la contrainte
appliquée σ au taux de déformation axiale de la colonne ε. A la
différence des pieux « classiques » pour lesquels le contraste de
rigidité pieu/sol est tel que l’essentiel des tassements est obtenu
en pointe, la particularité d’une colonne de soil-mixing réside
dans un contraste de rigidité colonne/sol plus faible et une
sensibilité notable de la raideur globale en tête vis-à-vis du
comportement local. Ces éléments ont justifié le recours à une
loi de contrainte-déformation non linéaire pour la colonne : il a
été retenu une loi de forme hyperbolique (Figure 10) construite
à l’aide de deux paramètres : le module sécant E
50
et la
résistance à la compression simple R
c
. Lors du présent exercice,
cette loi s’est révélée apte à retranscrire le comportement
observé, à la différence d’une loi linéaire élastique.
Asymptote = Rc
Rc
0,5 Rc
E
50
ε
σ
c
R E
50
2
1
Figure 10. Loi de contrainte-déformation retenue pour la colonne
4.2
Mise en œuvre
La loi de contrainte-déformation de la Figure 10 est construite à
partir des paramètres (E
50
, R
c
) qui Figurent dans le Tableau 2.
Les paramètres de pente des lois de Frank et Zhao (Figure
9) s’obtiennent par corrélation avec le module
pressiométrique E
M
:
K
t
= 0,8 E
M
/ B
et
K
p
= 4,8 E
M
/ B
, où
B
désigne le diamètre de la colonne. Ensuite, pour le choix du
frottement latéral limite q
s
, deux hypothèses enveloppes sont
examinées : la première est celle d’un contact béton/sol pour
laquelle la valeur de q
s
s’obtient par corrélation avec la pression
limite pl* ; la deuxième hypothèse est celle d’un contact sol/sol
pour laquelle la valeur de q
s
est celle du cisaillement limite de
Mohr Coulomb : q
s
= tan(φ’).K
0
.σ
v
’, avec K
0
= 0,5 et σ
v
’ la
contrainte verticale effective initiale à l’interface de la colonne.
Enfin, la contrainte limite en pointe q
p
est prise égale à 4 MPa.
3
1
2
3
4
Essai
E = f(σ) et q
s
= f(σ
v
’)
E = f(σ) et q
s
= f(pl*)
E = E
50
et q
s
= f(σ
v
’)
E = E
50
et q
s
= f(pl*)
Figure 11. Courbe de chargement – Modélisation analytique simplifiée
5
CONCLUSION
Les enseignements tirés de l’essai de chargement en vraie
grandeur ont permis d’orienter le choix des paramètres d’entrée
des différents outils numériques développés dans le cadre du
projet RUFEX. Les résultats obtenus, tant par les modèles
numériques que par le modèle semi-analytique, permettent de
bien reproduire le comportement observé lors de l’essai, aussi
bien sur le comportement avant rupture que sur le mode de
rupture. Ils mettent en évidence la nécessité de modéliser
correctement le comportement non linéaire du matériau sol-
ciment qui influe significativement sur le comportement global,
à la différence des pieux « rigides ».
6
REMERCIEMENTS
Les auteurs tiennent à remercier la DGCIS (Direction Générale
de la Compétitivité et des Services) et les Conseils Généraux de
la Région Ile de France et 93 qui cofinancent cette recherche.
7
REFERENCES BIBLIOGRAPHIQUES
D’Aguiar, S. C., A. Modaressi-Farahmand-Razavi, J. A. dos Santos, and
F. Lopez-Caballero (2011).
Elastoplastic constitutive modeling of
soil-structure interfaces under monotonic and cyclic loading
.
Computers and Geotechnics 38(-), 430447.
Frank, R. & Zhao, S. R. (1982),
Estimation par les paramètres
pressiométriques de l’enfoncement sous charge axiale des pieux
forés dans les sols fins
, Bull. Liaison Labo. P. et Ch. 119 :17-24.
Helwany S. 2000
Applied Soil Mechanics with ABAQUS Applications
,
J. WILEY & SONS, INC pp. 61-67
Hujeux, J. C. (1985).
Une loi de comportement pour le chargement
cyclique des sols en génie parasismique
, pp. 278–302. V.
Davidovici, Presses ENPC.


