2452
Proceedings of the 18
th
International Conference on Soil Mechanics and Geotechnical Engineering, Paris 2013
Table 1. Some soil properties and test conditions
Test
Soil
Plasticity
limit,
W
p
(%)
Liquid
limit,
W
L
(%)
Coefficient
of
consolidation
c
v
or
c
h
(m
2
/min)
C
c
e
0
σ'
v
0
(kPa)
p
vac
(kPa)
p
s
(kPa)
V-test
Ariake clay-1
60.3
120.5
2.3×10
-5
#
0.75
2.5
40*
80
80
R-test
Ariake clay-2
56.8
120.3
5.0×10
-6
-
-
0
80
80
*: Initial vertical effective stress in the sample; #: The value was obtained by fitting the measured consolidation rate;
: After pre-consolidation under
20 kPa pressure.
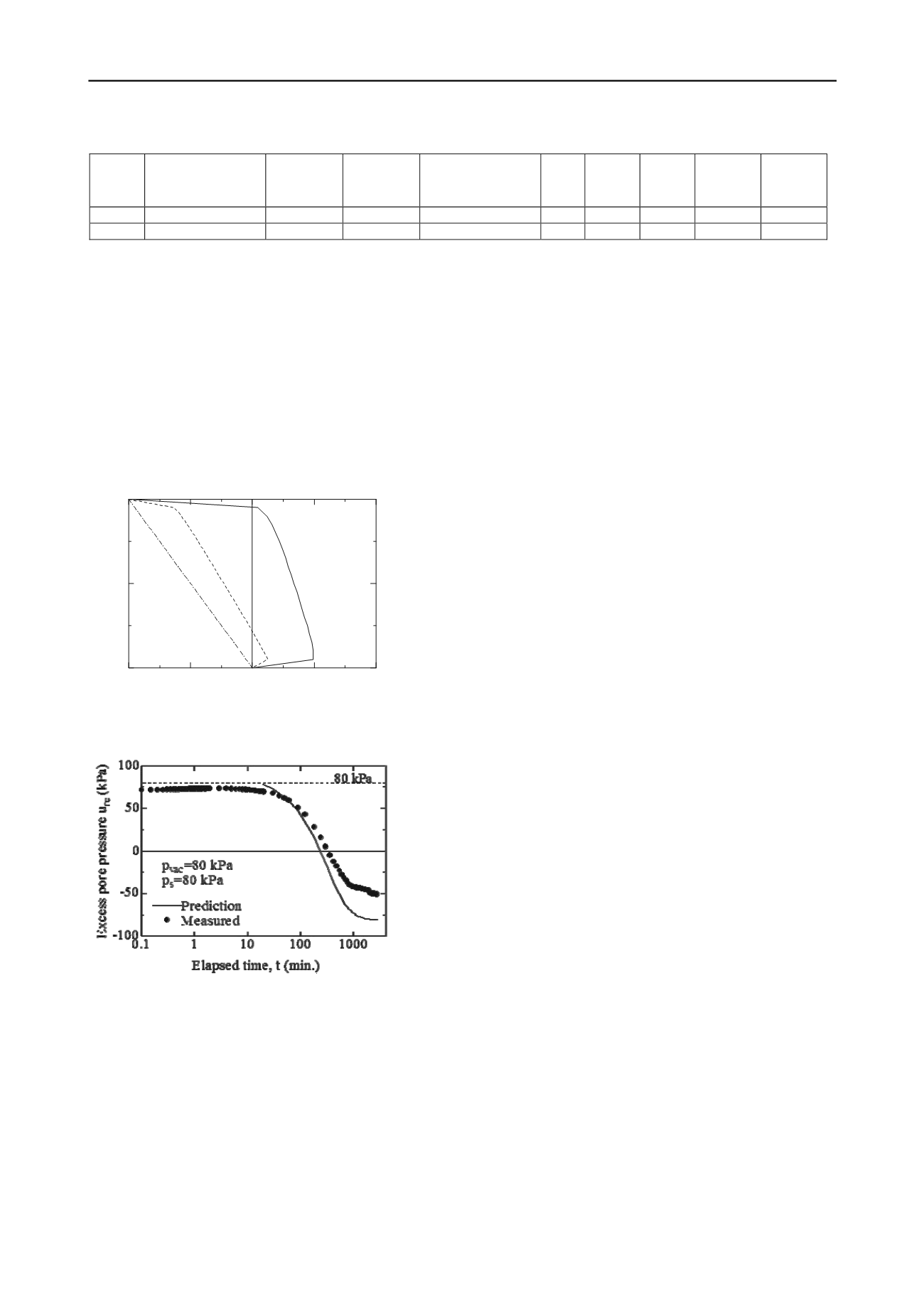
in Fig. 3. Except for the fact that the measured initial value of
u
b
of about 72 kPa is slightly lower than the 80 kPa applied
surcharge load, the prediction almost matches the measured data.
The slightly lower initial
u
b
value may indicate that the
specimen was not 100% saturated.
Although two-way drainage test was not conducted, using
the same soil parameters as for one-way drainage test, and
assuming the thickness of the soil sample is 20 mm, the
predicted excess pore water pressure (
u
) distribution within the
sample at different elapsed times are given in Fig. 4 to
demonstrate the capacity of the proposed theory.
-80
-40
0
40
80
0
10
20
Excess pore pressure, u (kPa)
Depth, D (mm)
1 min
3
15
p
vac
= 80 kPa
p
s
= 80 kPa
Figure 4. Predicted
u
variation in soil sample under two-way drainage
boundary condition
Figure5.Comparison of predicted and measured
u
re
3.2.2
R-test
The geometric parameters required to calculate the predictions
for this case are:
r
e
= 30 mm;
r
w
= 4 mm; and
l
= 20 mm. The
assumed radius of the smear zone,
r
s
= 7 mm; the hydraulic
conductivity ratio,
k
h
/
k
s
= 5;
k
h
= 10
-9
m/s; and
k
w
= 10
-4
m/s. In
the case of radial drainage, with Eqs. (16) and (17) the initial
condition of a uniform excess pore water pressure (
u
0
)
distribution in a unit cell is not satisfied (which is a particular
limitation of this theory). These equations only ensure that the
average initial value of
u
0
is the same as the applied value. The
predicted initial value at the periphery of the sample (unit cell)
is higher than the applied value. The predicted values are
compared with the measured data from the time at which the
predicted value at the periphery was equal to the applied initial
value. In the physical test at the corresponding time, the pore
water pressure at the periphery of the sample starts to reduce.
Comparison of the excess pore water pressures at the periphery
of the sample (
u
re
) is given in Fig. 5. For this case, during the
consolidation period the measured excess pore water pressure
initially decreased but then increased for a brief period before
finally exhibiting further dissipation. Furthermore, the
measured final excess pore water pressure did not reach the
applied vacuum pressure of 80 kPa. Nevertheless, the trends of
both the measured and the predicted dissipation curves are
similar.
From the above comparisons, it can be seen that the theory
provides reasonable predictions of the measured soil behaviour
and so it should be able to be used reliably for designing
preloading projects that adopt a combination of vacuum
pressure and surcharge load to consolidate the soil deposit.
4 CONCLUSIONS
A consolidation theory, expressed in closed-form equations, for
soil consolidation under the combination of a vacuum pressure
and a surcharge load has been developed for a uniform clayey
deposit with and without prefabricated vertical drain (PVD)
improvement. For cases without PVD improvement, both one-
way and two-way drainage boundary conditions have been
considered.
Laboratory consolidation tests were conducted, adopting a
combination of vacuum pressure and surcharge loading under
oedometer conditions with both vertical and radial drainage.
The excess pore water pressures measured in these test were
compared with values predicted by the suggested theory. It has
been demonstrated that the theory is valid and can be used for
designing preloading projects that adopt a combination of
vacuum pressure and surcharge load to pre-consolidate soft soil
deposits.
REFERENCES
Chai, J. C., Carter, J. P. and Hayashi, S. 2006. Vacuum consolidation
and its combination with embankment loading.
Canadian
Geotechnical Journal
43(10), 985-996.
Chai, J.-C., Matsunaga, K., Sakai, A. and Hayashi, S. 2009. Comparison
of vacuum consolidation with surcharge load induced consolidation
of a two-layer system.
Géotechnique
59(7), 637-642.
Chai, J.-C. and Carter, J. P. 2011.
Deformation analysis in soft ground
improvement
. Springer, p. 247.
Hansbo S. 1981. Consolidation of fine-grained soils by prefabricated
drains.
Proceedings of 10th International Conference on Soil
Mechanics and Foundation Engineering
, Stockholm 3, 677-682.
Hirata, M., Kitoh, M., Yamada, K., Iizuka, A. and Arai, K.
2010.Deformation behavior and counter measures of expressway
embankment on super-soft ground.
Journal of Japan Society of Civil
Engineers
66(2), 356-369 (in Japanese).
Indraratna, B., Rujikiatkamjorn, C., Ameratunga, J. and Boyle, P. 2011.
Performance and Prediction of Vacuum Combined Surcharge
Consolidation at Port of Brisbane.
Journal of Geotechnical and
Geoenvironmental Engineering
ASCE137(5), 550-554.
Kelly, R. B., Wong, P. K. 2009. An embankment constructed using
vacuum consolidation.
Australian Geomechanics
44(2), 55-64.
Terzaghi K. 1943.
Theoretical soil mechanics
. New York, John Wiley
and Sons.


