2447
Technical Committee 211 /
Comité technique 211
of the unit cell, the soil was modelled as elastic and the
encasement and the column as elastic-perfectly plastic.
3.2
Stress concentration
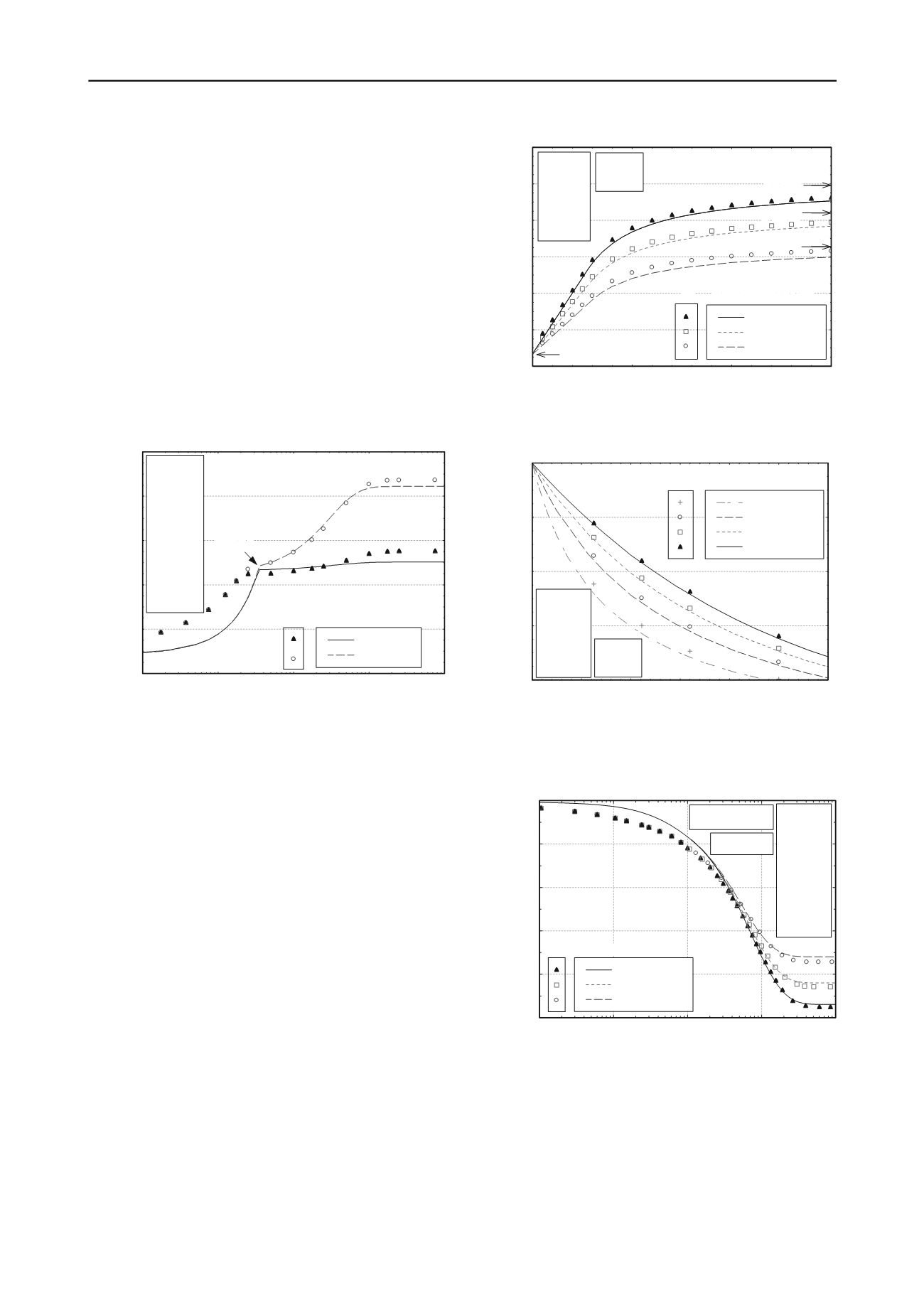
The ratio between the vertical stress on the column and on the
soil is usually called the stress concentration factor
(
SCF
=
σ
zc
/
σ
zc
) and gives an idea of the part of the applied load
that the soil transfers to the column. Figure 3 shows its variation
with time. The vertical stresses on the soil and on the column
may vary with the radius, and therefore, their averaged values
are used to calculate the
SCF
.
A higher encasement stiffness provides a better lateral
confinement to the column, and hence, the column supports a
higher load. A good agreement is found between the analytical
and the numerical results. However, as it happens for the stone
column solution (Castro and Sagaseta 2009), the agreement for
low degrees of consolidation (<30%) is not very good due to
inherent assumptions of Barron’s solution.
0
2
4
6
8
10
0.0001
0.001
0.01
0.1
1
J
g
/(
r
c
E
s
)=0
J
g
/(
r
c
E
s
)=2
FE Closed-form solution
Column
yielding
E
c
/
E
s
=40
E
s
=1 MPa
c
=
s
=0.3
a
r
=0.25
r
c
=0.5 m
c
=40º
c
=10º
K
0
s
=0.6
p
a
/(z
')=
10
Time factor,
T
r
SCF
,
zc
/
zs
Figure 3. Stress concentration on the column with time.
3.3
Settlement reduction
The settlement reduction decreases with the applied load,
p
a
,
from an elastic value,
e
, and approaches a plastic one,
p
, at
the same rate as plastic strains develop in the column (Figure 4).
The applied load is normalized by the initial vertical stress
because column yielding depends on that factor,
p
a
/(
L
'
s
).
On the other hand, the settlement reduction introduced by the
encasement is nearly the same for different area replacement
ratios (Figure 5), which means that column encasement is
equally useful for different area replacement ratios, yet columns
of smaller diameters are better confined. In Figures 4, 5 and 6,
the numerical results validate the accuracy of the analytical
solution, but the agreement gets slightly worse as the tensile
stiffness of the encasement increases. Hence, the only
assumption that has a slightly noticeable effect in the results is
neglecting the elastic strains in the column during its plastic
deformation. A future improvement of the analytical solution
including those elastic strains is currently being developed.
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0
0.5
1.0
1.5
J
g
/(
r
c
E
s
)=0
J
g
/(
r
c
E
s
)=0.75
J
g
/(
r
c
E
s
)=2
Closed-form solution
FE
'
s
=
'
c
K
0s
=0.6
p
=0.53
p
=0.62
p
=0.70
e
=0.233-0.235
E
c
/
E
s
=40
c
=
s
=0.3
a
r
=0.11
c
=40º
c
=10º
Normalised applied load,
p
a
/(
L
'
s
)
Settlement reduction factor,
Figure 4. Settlement reduction. Influence of the applied load.
0.2
0.4
0.6
0.8
1.0
0
0.05 0.10 0.15 0.20 0.25 0.30
J
g
/(
r
c
E
s
)=5
J
g
/(
r
c
E
s
)=2
J
g
/(
r
c
E
s
)=0.75
J
g
/(
r
c
E
s
)=0
Closed-form solution
FE
'
s
=
'
c
K
0s
=0.6
E
c
/
E
s
=40
c
=
s
=0.3
c
=40º
c
=10º
p
a
/(
L
'
s
)=1
Area replacement ratio,
a
r
Settlement reduction factor,
Figure 5. Settlement reduction. Influence of the encasement stiffness for
different area replacement ratios.
0
100
200
300
400
500
0.0001
0.001
0.01
0.1
1
J
g
/(
r
c
E
s
)=0
J
g
/(
r
c
E
s
)=0.75
J
g
/(
r
c
E
s
)=2
p
a
=100 kPa
'
c
=
'
s
=10 kN/m
3
E
c
/
E
s
=40
E
s
=1 MPa
c
=
s
=0.3
a
r
=0.11
c
=40º
c
=10º
L
=10 m
K
0s
=0.6
FE Closed-form solution
Time factor,
T
r
Settlement,
s
z
[mm]
Figure 6. Time-settlement curve.
3.4
Encasement length
The effectiveness of encasing the columns in reducing the
settlement is directly related to the tensile stress of the
encasement, which provide lateral support to the column. Some
authors (e.g. Khabbazian et al. 2010, Gniel and Bouazza 2009,
Murugesan and Rajagopal 2006) have proposed a partial
encasement of the columns, limiting it to the upper part where


