2337
Technical Committee 209 /
Comité technique 209
-150
-100
-50
0
50
100
150
0
0.5
1
1.5
2
2.5
u
t
[cm]
(c)
q
s
[kPa]
Figures 2. Modélisation d’essai de cisaillement suivant différentes
conditions (a : déplacement symétrique, b : déplacement non symétrique
– relaxation, c : déplacement non symétrique – relaxation nulle)
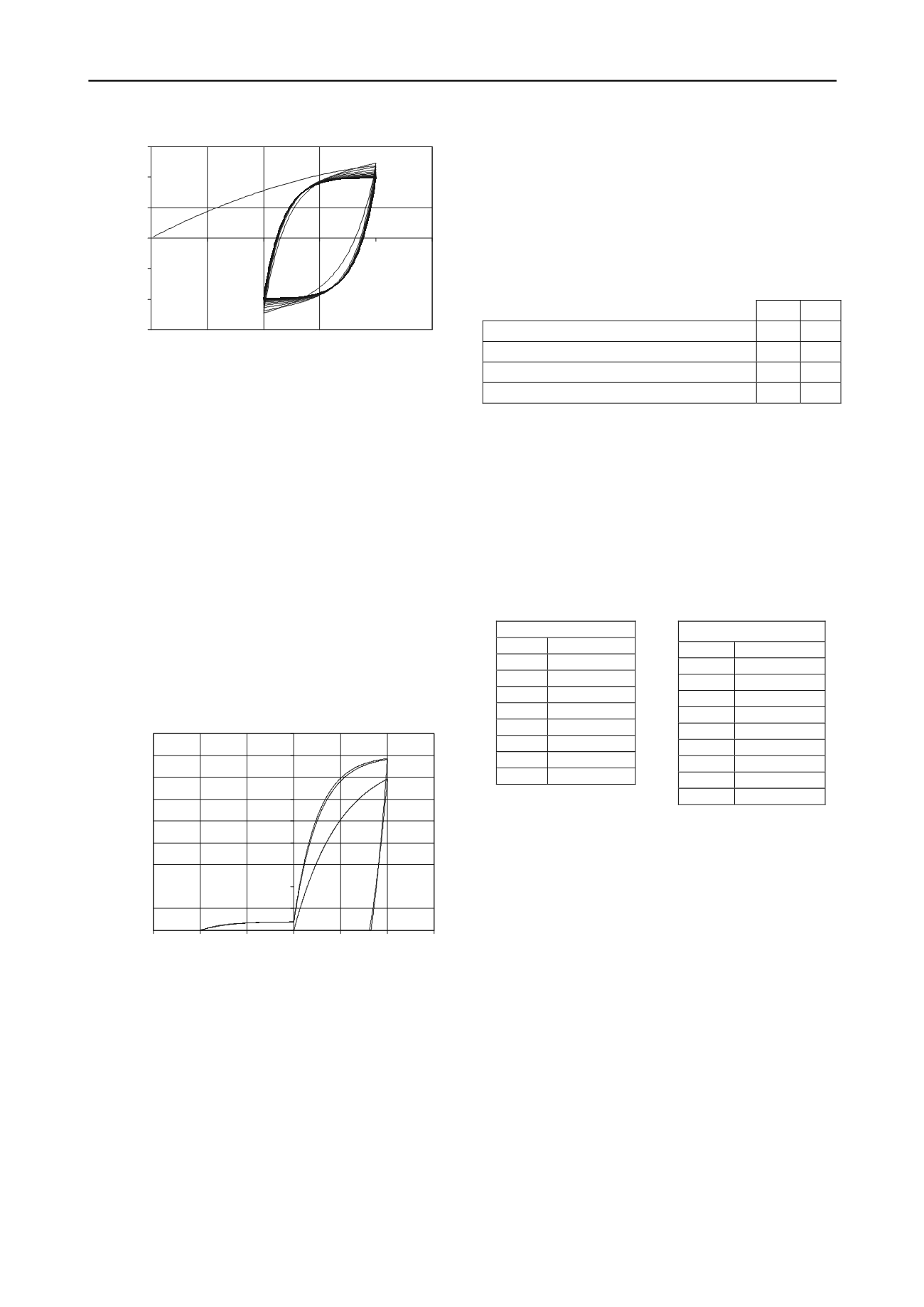
2.3 Comportement de la base du pieu
La loi utilisée pour modéliser l’enfoncement de la base d’un
pieu u
p
a été développée sur le même modèle que la loi
précédente. Elle est formulée directement en termes d’effort
axial mobilisable sous la base du pieu et comprend neuf
paramètres dans sa version la plus évoluée. Pour des
chargements monotones, les paramètres Q
p0
et
sont toujours
calés respectivement selon la norme française d’application de
l’Eurocode 7 relative aux fondations profondes (AFNOR 2012)
et selon les lois de Frank et Zhao (1982).
Un paramètre complémentaire p
r
(variant entre 0 et 1) a été
introduit de manière à prendre en compte le fait que la pointe
d’un pieu sollicitée axialement peut se trouver au-dessus de sa
position d’origine. Plus il est faible, moins l’effort mobilisé sous
la pointe du pieu, tant que ce dernier est au-dessus de sa
position initiale, est important (Figure 3).
0
200
400
600
800
1000
1200
1400
1600
1800
-3
-2
-1
0
1
2
3
u
p
[cm]
Q
p
[kN]
Figure 3. Modélisation de la mobilisation de l’effort de pointe
3 PRÉSENTATION DES ESSAIS EN CENTRIFUGEUSE
Le modèle réduit considéré, à l’échelle du 1/23
ème
, est soumis à
une accélération centrifuge de 23×g. Les propriétés du sable
sont les suivantes (Jardine
et al.
2009, Andria-Ntoanina
et al.
2010) :
dmin
= 1395-1408 kg/m
3
,
dmax
= 1755 kg/m
3
,
s
= 2650
kg/m
3
, d
10
=0,15 mm, d
50
=0,207-0,210 mm, d
60
=0,23 mm et
CU=1,49-1,43. Le pieu modèle a les caractéristiques suivantes :
forme cylindrique « pointe » plate, diamètre de 18 mm,
longueur de 590 mm, fiche de 560 mm, barreau d’aluminium de
masse totale 0,405 kg, rugosité à l’état « neuf » définie par
R
t
=112 μm, R
a
=25,9 μm soit R
t
/d
50
=0,54 et R
a
/d
50
=0,13,
rugosité à l’état « usé » (après 10 essais) définie par R
t
=90 μm,
R
a
=23,9 μm soit R
t
/d
50
=0,44, R
a
/d
50
=0,12. Les massifs sont
reconstitués par pluviation de sable sec dans un conteneur
double (Figure 4).
Les expérimentations réalisées comprennent deux séries
d’essais monotones permettant de déterminer la résistance
ultime du pieu en compression (Q
p
) et en traction (Q
s
). Quatre
essais cycliques ont ensuite été réalisés : la charge atteint
d’abord la valeur V
m
puis oscille entre V
max
= V
m
+ V
c
et V
min
=
V
m
- V
c
(Tableau 2).
Tableau 2. Programme de chargement des essais cycliques
V
m
/Q
p
V
c
/Q
p
Essai 1 (traction cyclique)
-0,33 0,05
Essai 2 (traction cyclique)
-0,133 0,133
Essai 3 (cyclique alterné – compression dominante)
0,3
0,4
Essai 4 (cyclique alterné)
0
0,133
4 ANALYSE DES RÉSULTATS OBTENUS
4.1 Présentation des résultats
Les paramètres de calcul (Tableau 3) sont calés sur les deux
essais monotones en traction (Figure 4) et en compression
(Figure 5) en supposant le module de Young du pieu égal à 10
GPa et sur l’essai cyclique 3 qui présente le comportement
a
priori
le plus complexe à modéliser.
Tableau 3. Propriétés des paramètres de la loi t-z pour le frottement
axial et pour la résistance de pointe
Frottement axial
q
s0
102 kPa
1 cm
30 kPa
1,8 cm
2
q
s
- 83 kPa
25 cm
20
0,05
Résistance de pointe
Q
p0
1615 kN
0,1 cm
___
___
___
Q
p
300 kN
5 cm
6
0,1
p
r
0,05
4.2 Analyse des résultats
La figure 6 propose, pour les quatre essais, la comparaison entre
les résultats expérimentaux et les résultats numériques.
Expérimentalement, la rupture du pieu est obtenue pour les
essais 2, 3 et 4 avec un défaut de résistance à la traction du sol.
Pour l’essai 1, alors que l’effort de traction appliqué est plus
important de tous les essais réalisés, la rupture n’a pas été
atteinte pour le nombre de cycles effectués. Il est néanmoins
très probable que le nombre de cycles effectués est insuffisant.
Pour l’essai 3, la rupture en compression peut être observée
puisque l’enfoncement du pieu est supérieur à 10 % de son
diamètre. Les efforts de traction atteints traduisant la rupture du
pieu pour les essais 2, 3 et 4 sont très différents : 1204,6 kN,
843,22 kN et 317 kN. Ce résultat montre que le frottement
mobilisable le long du fût du pieu, après un grand nombre de
cycles de chargement, varie en fonction du chargement
appliqué. Dans l’état actuel, la loi t-z proposée n’est pas en
mesure de rendre compte ce phénomène car les paramètres
q
s
et u
ts
ne traduisent pas suffisamment les effets des cycles sur la
résistance de l’interface.
Les résultats obtenus indiquent toutefois que le modèle
développé rend compte de manière plutôt satisfaisante des
déplacements du pieu lors des premiers cycles de chargement.
Pour des nombres de cycles élevés, les tendances restent plutôt
bien appréhendées même si les amplitudes de déplacement ne
sont pas correctes.


