2248
Proceedings of the 18
th
International Conference on Soil Mechanics and Geotechnical Engineering, Paris 2013
stochastic nature of the algorithm showing value convergence
with increasing generations is reflected in all the results.
5 CONCLUSIONS
0.00001
0.01
10
10000
10000000
0
2
4
6
8
10
12
14
16
18
20
22
24
26
28
30
32
34
36
38
40
42
44
46
48
50
Population Fitness
F
(x)
i
Generation Number
Av. Fitness of Random Population
Std. Dev. of Fitness of Random Population
Variance of Fitness of Random Population
Fitness (
F
i
)=FOS
max.
-FOS
i
(WINDOWING TECHNIQUE)
Fig.6. Change in average fitness, standard deviation & variance of
population fitness function with successive generations.
0.01
0.1
1
10
100
1000
10000
100000
0.005
0.05
0.5
Max. Fitness
=
F
(
x)
max.
=
f(x)
max.
-f(x)
i
i
=G
i
(1-r)
(Gi-1)
i
= Size Reduction Parameter,
G
i
= Generation Number,
r = A constant =0.1 (assumed)
A global population based search procedure (APMA) is
developed and successfully applied to slope-stability problem. It
does not require problem specific knowledge in searching the
critical slip-surface of a soil-slope and is a heuristic technique
based on the ‘generate-and-test’ strategy. Diverse aspects are
presented to demonstrate its efficiency and robustness. The
spectrum of application area of APMA is widespread as it is a
direct search method where no specific search direction is used
and multivariable functions, both continuous and discontinuous
can be handled. Function value evaluations at discrete points
only enable it to handle non-differentiable functions at ease.
The beauty of the process is that, it handles a number of designs
in each simulation run. The result of some simulation runs
revealed minimum factor of safety obtained by APMA is less
than that found by directed grid search, variational method, GA
and GA-SA hybrid.
Fig.7. Max
m
. fitness of each gen. vs. search space size red. parameter.
0.98
1.00
1.02
1.04
1.06
1.08
1.10
1.12
1.14
1.16
1.18
1.20
0
2
4
6
8
10
12
14
16
18
20
22
24
26
28
30
32
34
36
38
40
42
44
46
48
50
Min. Obj. Func. = f(x) min. =
FoSmin.
Generation Number
1st Simulation Run
2nd Simulation Run
3rd Simulation Run
4th Simulation Run
5th Simulation Run
QUICK RANDOMMOVEMENT TOGLOBALOPTIMUM
Fig.8. Stochastic movement of Min. FOS (obj. func.) in successive
gens. to converge to global optimum (Results of five simulation runs).
9.6317, 63.7615
7.2727, 57.5073
7.9765, 59.6188
0
20
40
60
80
100
120
140
160
180
-20
-10
0
10
20
30
40
50
60
70
Design Variable,CY
Design Variable, CX
G1 G2 G25 G50
0
0.2
0.4
0.6
0.8
1
1.2
1.4
1.6
1.8
0
20
40
60
80
100
120
140
160
180
Design Variable, N
d
Design Variable,CY
G1 G2 G25 G50
Fig.9. CX vs. CY & CY vs. N
d
: The artificial intelligent character
depiction. Fast random movement of candidate solutions to best part of
the search space with increasing generations.
0.001
0.01
0.1
1
10
100
1000
10000
100000
0
2
4
6
8
10
12
14
16
18
20
22
24
26
28
30
32
34
36
38
40
42
44
46
48
50
Max. Fitness of Population
in Each Generation (
F
max
. )
Generation Number
1st Simulation Run
2nd Simulation Run
3rd Simulation Run
4th Simulation Run
5th Simulation Run
Fitness (
F
i
)=FOS
max.
-FOS
i
(WINDOWING TECHNIQUE)
Fig.10. Stochastic decrease of maximum fitness in successive
generations (Results of five simulation runs superimposed).
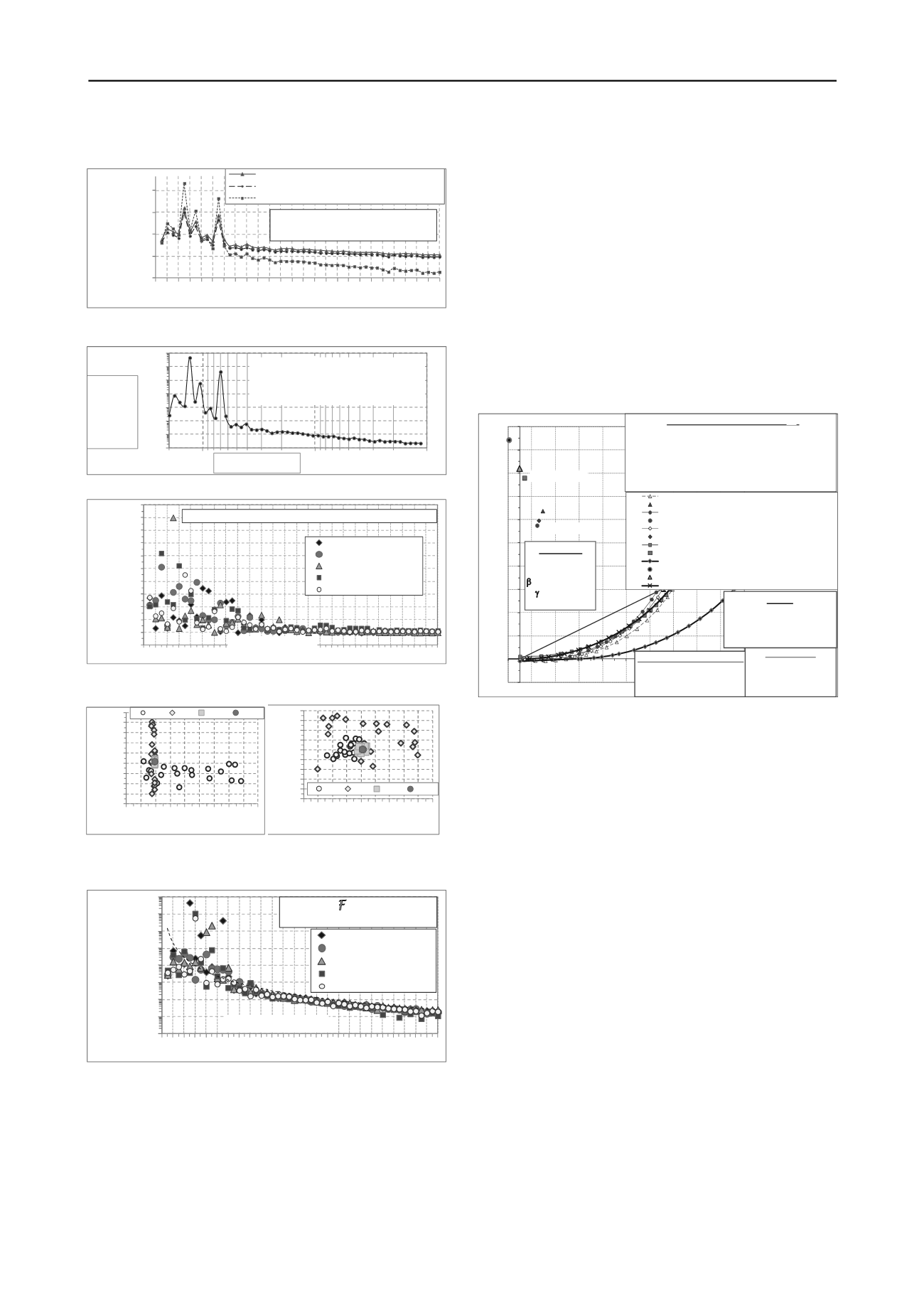
Fig.9 depicts the artificial intelligent character of the
algorithm wherein a fast random movement of candidate
solutions with increasing generations to best part of the search
space is noticed. Fig.10 shows the stochastic decrease of
maximum fitness in successive generations in 5 simulation runs.
Fig.-11 gives the validation of results against other studies
reported in literature.
1.9062, 77.9340
-4.662756598,
94.31524927
-0.143410414,
81.98342133
-10
0
10
20
30
40
50
60
70
80
90
100
-5 5 15 25 35 45 55 65 75 85 95
Height inmetres
Distance in metres
Spencer Arc
Spencer Center
GA Arc-Toe Slide(n=64, Generation=24th)
GA Center-Toe Slide(n=64, Generation=24th)
GA Arc-Toe Slide (n=20, Generation=4th)
GA Center-Toe Slide(n=20, Generation=4th)
GA Arc (n=20, Generation=70th)
GA Center (n=20, Generation=70th)
GA-SA Hybrid: Arc (n=20, Generation=37th)
GA-SA Hybrid: Centre (n=20, Generation=37th)
APMA Centre (n=20, Generation=49th)
APMA Arc (n=20, Generation=49th)
Minimum Factor of Safety (FOS
min
)
Spencer(1967) :1.07
Narayan et.al.(1976):1.13
Saha (2003):GA(ToeSlide-2Variables) (n=20,Gen.=25) :1.05
Saha (2003):GA(ToeSlide-2Variables) (n=64,Gen.=25) :1.04
Saha (2011):GA (3 Variables) (n=20,Gen.=75):1.0104
Saha (2011):GA-SAHybrid (3 Variables) (n=20,Gen.=75):1.00249
Present Study:APMA (3 Variables) (n=20,Gen=50):0.9993828
SOIL DATA
B = 60 m
H = 30 m
= 26.50 deg.
c
/
/
H= 0.02
r
u
= 0.50
GA
(RouletteWheelSelection)
CX=1.906, CY=77.934
N
d
=0.965,R=f(CX,CY,N
d
) =76.87
FoS=1.0104
GA-SA Hybrid
APMA
CX=-0.14341, CY=81.983421,
N
d
=0.9998627
R=f(CX,CY,N
d
)=81.979442
FoS=0.9993828
CX=-4.663, CY=94.315
N
d
=0.995
R=f(CX,CY,N
d
) =94.304
FoS=1.00249
Fig.11. Comparison of results obtained by various methods.
6 REFERENCES
A.Hedar. Test function web pages,
-
u.ac.jp/member/student/hedar/Hedar_files/TestGO_files/Page364.htm
Bishop A.W. 1955. “The use of slip circles in the stability analysis of
slopes”, Geotechnique. Vol.-5, 7-17.
Deb Kalyanmoy 2000.
Optimization for Engineering Design,
Algorithms and Examples
, Prentice Hall, New Delhi, India.
Duncan J.M. 1996. State of the art: limit equilibrium and finite-element
analysis of slopes, Journal of Geotec. Eng.,ASCE, 122(7), 577-596.
Li K.S., Z. Shangguan, H. Duan, Y Liu, M. Luan 2009. Searching for
critical failure surface in slope stability analysis by using hybrid
genetic algorithm, Geomechanics and Engg., 1(1), 85-96.
Malkawi A.H., Hassan W.F., and Sarma S.K. 2001. Global search
method for locating general slip surface using Monte Carlo
techniques, Journ. of Geotech. & Geoenv. Engg., 127(8), 688-398.
Narayan C.G.P., Bhatkar V.P. & Ramamurthy T. 1976. Slope stability
analysis by variational method, Indian Geotech. J., Vol.- 6, 68-90.
Saha Abhijit 2003. Genetic algorithm based search in slope stability
analysis, Proc. of 12
th
Asian Regional Conference in Soil Mech. &
Geotechnical Engg., Singapore, Vol.-I, 981-984.
Saha Abhijit 2011. Genetic algorithm based search coupled with
Boltzmann selection in locating the critical surface in slope
stability, Proc. of 14
th
Asian Regional Conference in Soil Mech. &
Geotechnical Engg., Hong Kong, Paper No.-115.
T. Beielstein 2003. Tuning evolutionary algorithms/Overview &
Comprehensive Introduction. Tech. Report 148/03, Universität
Dortmund, Germany.
Spencer E. 1967. A method of analysis of the stability of embankments
assuming parallel inter-slice forces, Geotechnique, London, Vol.-
17, 11-26.
X.-S. Yang 2010.
Test problems in optimization, in: Engineering
Optimization: An Introduction with Metaheuristic Applications
(Eds Xin-She Yang)
, John Wiley & Sons.


