2160
Proceedings of the 18
th
International Conference on Soil Mechanics and Geotechnical Engineering, Paris 2013
areas with different volumes were considered (Table 1). The
initiation of the debris flow is assumed to be caused by soil slips
and the flows are unchanneled along most of the path. The unit
weight of debris flow was set to the same value as in the case of
Faucon. The total duration for each simulation was 500 s. The
Voellmy model was used in the run-out analysis.
In total, 5,000 simulations were carried out associated to the
corresponding set of input parameters sampled from the
Gaussian
copula.
For
each
simulation
Table 1 Release volume used for the Monte Carlo simulation for the
three different release areas in the Tresenda village
Release Volume (m
3
)
Release area 1
1424
Release area 2
1410
Release area 3
1518
Total released volume
4352
the maximum flow heights and maximum velocities were
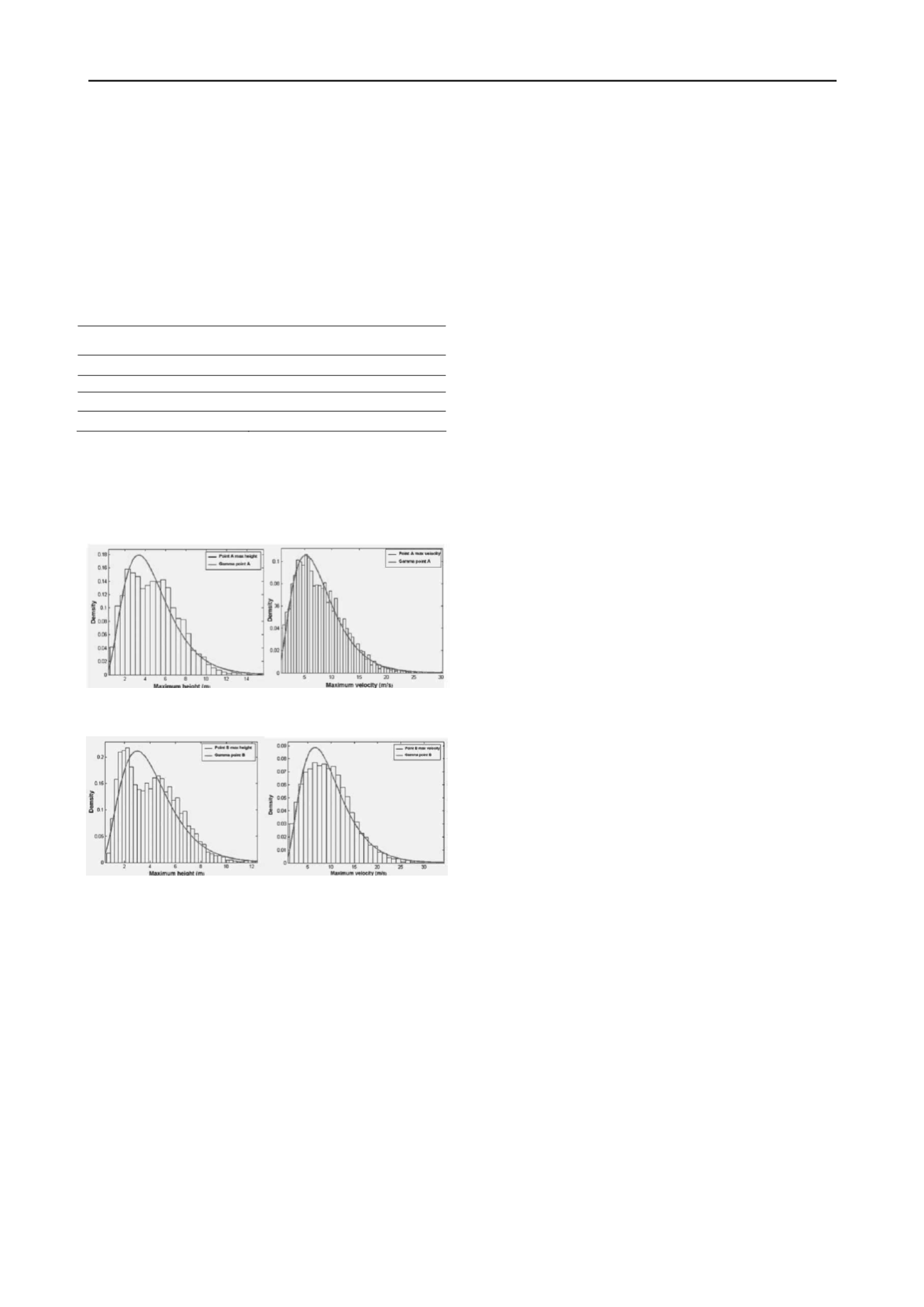
reported for each point. Also in the Tresenda case, a Gamma
distribution had the best fit to the output parameters. Figures 7
and .8 show the results for the maximum flow height and
velocities calculated in points A and B.
Figure 7. Gamma distribution fitted to the maximum height
(left) and velocities (right) values obtained in point A.
Figure 8. Gamma distribution fitted to the maximum height
(left) and velocities (right) values obtained in point B.
The results for the Tresenda case study were compared with
events in 1983 and 2002. In these incidents, only information
regarding the flow heights was available (no velocities were
estimated for these events). In the Tresenda case, the mean
value of the flow height in point A is overestimated compared
to the actual event while point B has a lower mean value than
the observed event. In the Tresenda case the simulated values
are closer to the actual events than in the Faucon case. This can
be possibly attributed to the potential of the Voellmy rheology
to model consistently these types of events.
5 CONCLUSIONS
The Monte Carlo method offers the advantage of modelling the
probability distributions of the intensity parameters from run-
out simulations. Of course, the reliability of the fitted
probability density functions for the input parameters strongly
depends on the completeness and accuracy of the original back-
analyses included in the collected database. Another limitation
of this study is that the estimated probabilities do not explicitly
account for the temporality of the phenomena.
For future
assessments it is recommended that run-out simulations using a
stochastic approach become a routine practice in order to
produce adequate future hazard scenarios and quantify the
uncertainty due to the input parameters. This will result in
intensity maps that are easier to interpret for end users,
especially within a probabilistic framework for landslide
mitigation.
6 ACKNOWLEDGEMNETS
The authors would like to thank Jean Philippe Malet and
Alexandre Remaître from the University of Strasbourg for the
data of the Faucon catchment.
7 REFERENCES
Begueria S., van Asch Th.W.J., Malet J.-P., Grondahl S. 2009. A GIS-
based numerical model for simulating the kinematics of mud and
debris flows over complex terrain.
Nat. Hazards and Earth Syst.
Sci
., 9, pp. 1897-1909.
Cancelli A. and Nova R.. 1985. Landslides in soil debris cover triggered
by rainstorms in Valtellina (Central Alps – Italy). In: Proceedings
of 4th International Conference and Field Workshop on
Landslides. The Japan Geological Society, Tokyo, pp. 267–272.
Crosta G.B., Dal Negro P., Frattini P. 2003. Soil slips and debris flows
on terraced slopes.
Nat. Hazards and Earth Syst. Sci.
, 3, 31- 42.
Guzzetti F., Crosta G., Marchetti M., Reichenbach P. 1992. Debris
flows triggered by the July, 17–19, 1987 storm in the Valtellina
area (Northern Italy). International Symposium Interpraevent 1992,
Bern, Switzerland, pp. 193-203
Hungr O. and McDougall S. 2009. Two numerical models for landslide
dynamic analysis.
Computers & Geosciences
35, pp. 978–992.
Hürlimann M., Medina V., Bateman A., Copons R., Altimir J. 2007.
Comparison of different techniques to analyse the mobility of
debris flows during hazard assessment-Case study in La Comella
catchment, Andorra. In Chen & Majors (eds.) Debris-Flow Hazard
Mitigation :Mechanics, Prediction and Assessment. Millpress,
Netherlands, pp. 411-422.
Karssenberg, D., Burrough, P. A., Sluiter, R., De Jong, K. 2001. The
PCRaster software and course materials for teaching numerical
modelling in the environmental sciences.
Transactions in GIS
, 5(2),
pp. 99-110.
Metropolis N. 1987. "The beginning of the Monte Carlo method". Los
Alamos Science (1987 Special Issue dedicated to Stanisław Ulam):
125–130.
Remaître A., Malet J.-P., Maquaire O. 2005. Morphology and
sedimentology of a complex debris flow in a clay-shale basin.
Earth Surf. Process. Landforms
30 pp.339-348.
Remaître A. 2006. Morphologie et dynamique des laves torrentielles:
Applications aux torrents des Terres Noires du bassin de
Barcelonnette (Alpes du Sud). Ph.D. thesis.
Remaître A., van Asch Th.W.J., Malet J.-P., Maquaire O. 2008.
Influence of check dams on debris flow run-out intensity
. Nat.
Hazards Earth Syst. Sci
. 8, pp. 1403-1416.
Remaître A., Malet J.-P., Maquaire O. 2009. Sediment budget and
morphology of the 2003 Faucon debris flow (South French Alps):
scouring and channel-shaping processes.Proc. Landslide Processes:
from geomorphological mapping to dynamic modelling, pp. 75-80.


