1750
Proceedings of the 18
th
International Conference on Soil Mechanics and Geotechnical Engineering, Paris 2013
0
30
60
90
120
150
180
0
2
4
6
8
1
v
(kPa)
h
(m)
0
overburden
50 MPa
100 MPa
200 MPa
1 000 MPa
10 000 MPa
30 000 MPa
60 000 MPa
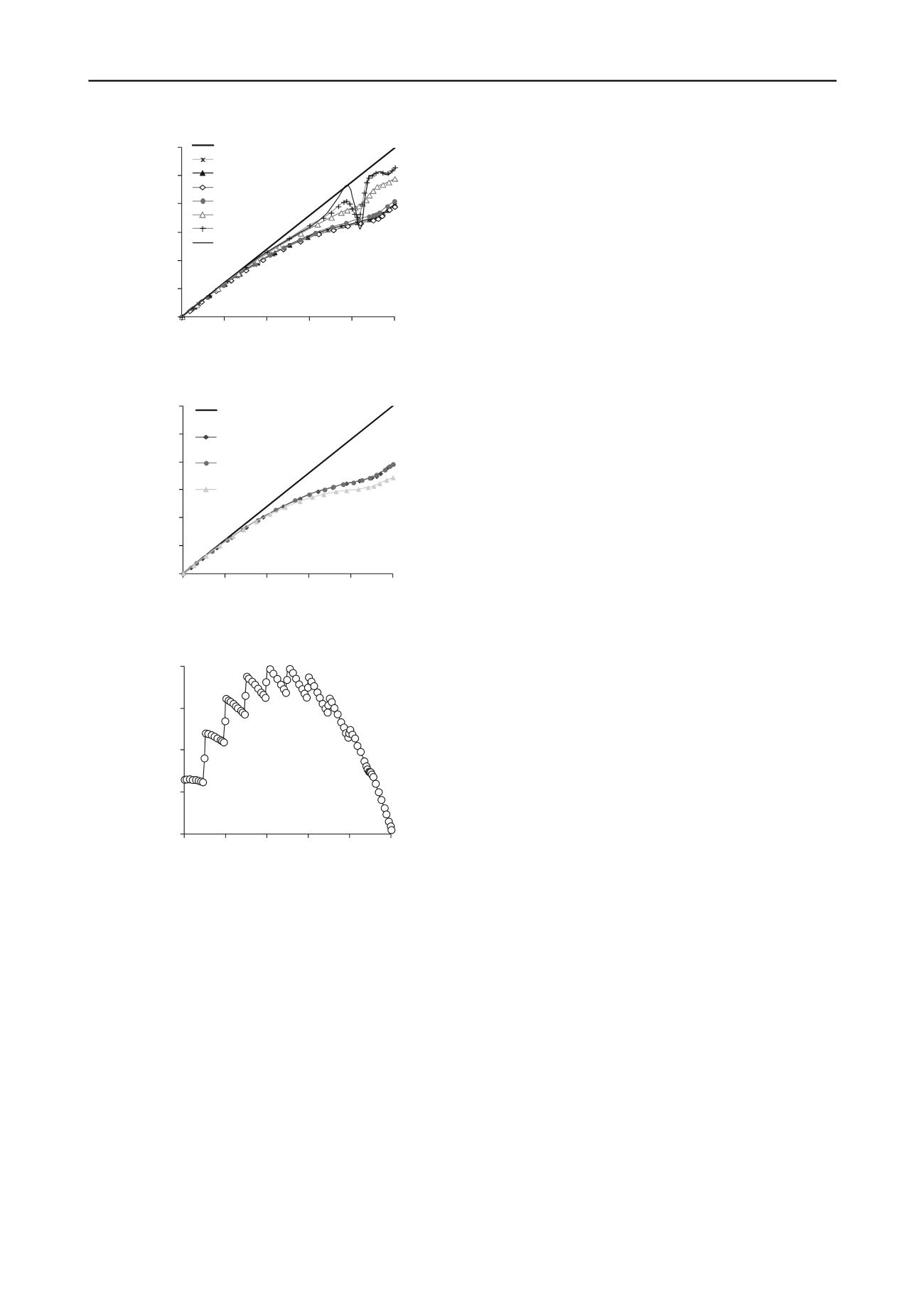
Figure 9. Vertical stress distribution along the VCL for different
Young's modulus of the backfill
E
b
; details are given in Table 1.
0
30
60
90
120
150
180
0
2
4
6
8
1
v
(kPa)
h
(m)
0
overburden
0.2
0.25
0.35
Figure 10. Vertical stress distribution along the VCL for different
Poisson's ratio of the backfill
b
; details are given in Table 1.
0
0.4
0.8
1.2
1.6
0
2
4
6
8
1
Vertical displacement (mm)
h
(m)
0
Figure 11. Vertical displacement distribution along the VCL for filling
in 10 layers; case shown in Figure 3, with details given in Table 1.
4 DISCUSSION AND CONCLUSION
In this paper, influencing factors related to trench geometry and
properties of the backfill are investigated using numerical
simulations to assess their effect on the vertical stress
distribution.
The results show that the most influential factors are the
walls inclination angle, trench width, and backfill cohesion,
friction angle and stiffness. The vertical stress distributions
along the VCL of trenches are less sensitive to variations of the
Poisson's ratio and dilation angle of the backfill.
The Young's modulus of the backfill may also significantly
influence the vertical stress distribution when its value is larger
than about 1/30
th
of that of the material along the walls. Below
this value, the vertical stress distribution can be considered
insensitive to the backfill stiffness.
It is finally noted that most of the vertical stress distributions
along the VCL show an upward curvature at
h
~ 8 to 9 m,
followed at greater depth by a quasi-linear trend (almost parallel
to the overburden pressure). This indicates a reduced stress
transfer near the base of the trench. Figure 11 shows the vertical
displacements along the VCL for a trench filled in 10 layers
(case shown in Figure 3). It is seen that the displacements of the
backfill tend to increase with depth
h
from the surface down,
reaching a maximum near mid-height of the trench. Below, the
vertical displacements decrease with depth, becoming nil at the
base of the trench. This behavior is associated with a decrease
of the downward displacements that is due in part to the
narrowing geometry of the opening and presence of the trench
floor, and which reduces the shear strains (and stresses) along
the fill-wall interfaces. In turn, this leads to a less pronounced
arching effect and an increase of the vertical stresses. This
explains, at least partially, the tendencies observed on the
results presented above.
5 ACKNOWLEDGEMENTS
The authors acknowledge the financial support of the NSERC
(RGPIN). The authors also received financial support from the
Industrial NSERC Polytechnique-UQAT Chair on Environment
and Mine Wastes Management.
6 REFERENCES
Blight G.E. 2006.
Assessing loads on silos and other bulk storage
structures: Research applied to practice
. Taylor &
Francis/Balkema, The Netherlands.
Goel S. and Patra N.R. 2008. Effect of arching on active earth pressure
for rigid retaining walls considering translation mode.
ASCE
International Journal of Geomechanics
8(2), 123–133.
Handy R.L. and Spangler M.G. 2007.
Geotechnical engineering: soil
and foundation principles
. McGraw-Hill.
Itasca Consulting Group, Inc. 2002.
FLAC - Fast Lagrangian analysis
of continua, User’s Guide
. Itasca, Minneapolis, MN.
Janssen H.A. 1895. Versuche über Getreidedruck in Silozellen.
Zeitschrift Verein Ingenieure
39, 1045-1049.
Li L. and Aubertin M. 2008. An improved analytical solution to
estimate the stress state in sub-vertical backfilled stopes.
Canadian
Geotechnical Journal
45(10), 1487-1496.
Li L. and Aubertin M. 2009a. Influence of water pressure on the stress
state in stopes with cohesionless backfill.
Geotechnical and
Geological Engineering
27(1), 1-11.
Li L. and Aubertin M. 2009b. A three-dimensional analysis of the total
and effective normal stresses in submerged backfilled stopes.
Geotechnical and Geological Engineering
27(4), 559–569.
Li L. and Aubertin M. 2009c. Numerical investigation of the stress state
in inclined backfilled stopes.
ASCE Int. J. Geomech.
9(2), 52-62.
Li L. and Aubertin M. 2010. An analytical solution for the nonlinear
distribution of effective and total stresses in vertical backfilled
stopes.
Geomechanics and Geoengineering
5(4), 237 — 245.
Li L., Aubertin M. and Belem T. 2005. Formulation of a three
dimensional analytical solution to evaluate stresses in backfilled
vertical narrow openings.
Can. Geotech. J.
42, 1705-1717.
Li L., Dubé J.-S. and Aubertin M. 2012a. An extension of Marston’s
solution for the stresses in backfilled trenches with inclined walls.
Geotechnical and Geological Engineering
(under evaluation).
Li L., Dubé J.-S. and Zangeneh-Madar Z. 2012b. Estimation of total and
effective stresses in trenches with inclined walls.
International
Journal of Geotechnical Engineering
6(4), 525-538.
Marston A. 1930. The theory of external loads on closed conduits in the
light of latest experiments. Bulletin No. 96,
Iowa Engineering
Experiment Station
, Ames, Iowa.
Singh S., Sivakugan N. and Shukla S.K. 2010. Can soil arching be
insensitive to
?
ASCE Int. J. Geomech.
10(3), 124–128.
Ting C.H., Shukla S.K. and Sivakugan N. 2011. Arching in soils applied
to inclined mine stopes.
ASCE Int. J. Geomech.
11(1), 29-35.
Thompson B.D., Bawden W.F. and Grabinsky M.W. 2012. In situ
measurements of cemented paste backfill at the Cayeli Mine.
Canadian Geotechnical Journal
49, 755–772.
Whidden W.R. 2009.
Buried flexible steel pipe: Design and structure
analysis
. ASCE Manuals and Reports on Engineering Practice, 119.


