1716
Proceedings of the 18
th
International Conference on Soil Mechanics and Geotechnical Engineering, Paris 2013
The presently available methods have several disadvantages
including (1) computational efficiency is low when they are
used to computing seismic response of super-long immersed
tunnels; (2) the effects of frequencies of excitation on
foundation impedances cannot be considered; (3) inertia of
tunnels is often neglected in most methods. This paper presents
a modified response displacement method in the frequency
domain so as to overcome the defects in the present analysis
methods.
2 RESPONSE DISPLACEMENT METHOD BY JSCE
The response displacement method introduced here is based on
a mass-spring model presented by the JSCE in 1988. It is
assumed in this model that shear motion is the main vibration
mode of strata on bedrock under seismic loading. In addition,
there is another assumption that self-vibration characteristics of
soil layers are not influenced by the existence of the tunnel. The
soil around the immersed tunnel along the longitudinal direction
is modeled as a series of particles. The springs and dashpots are
used to connect adjacent particles, as well as particle and
bedrock. The multi-segment tunnel is modeled as a beam with
longitudinal translational springs located at segment joints. The
segments and its surrounding soil particles are connected
through calibrated interaction springs and dashpots (Fig. 2).
k
k
-1
k
+1
L
k
L
k-1
L
k+1
K
1
K
2
K
3
M
e
Figure 2. Mass-spring model under longitudinal seismic loading
The response displacement method is a pseudo-static analysis
approach and consists of two steps: (1) determining the free-
field ground seismic deformation without considering the
presence of tunnel; (2) imposing the ground deformation
obtained in step one on the tunnel structure as a static load. The
computational process in detail is described as follows.
3 SEISMIC DEFORMATION OF FREE FIELD
Seismic deformation of free field can be derived by solving
dynamic equilibrium equation of the mass-spring model.
According to D'Alembert principle, the dynamic equilibrium
equation can be expressed as
g s
s
s
s s
uM uK uC uM
(1)
where
M
s
,
C
and
K
= lumped mass coefficient, damping
coefficient and stiffness coefficient, respectively;
u
s
= response
displacement of soil particles; and
u
g
= seismic acceleration at
the base of bedrock. The elements of tridiagonal symmetric
stiffness matrix are expressed as
1 1
2
3
11
k
k k
(2)
,
3
2
2
1 ( 2,3, , -1)
i i
k k i k i k i
i
n
(3)
1
2
3
nk nk k
nn
,
(4)
) , ,,
(
-,
n
i
i k
k
ii
32 1
2
1
(5)
where
k
3
= spring between soil particle and bedrock;
k
2
= spring
between adjacent soil particles;
i
= the number of the soil
particle; and
n
= number of soil particles.
Seismic displacement of the free-field soil at the base of the
immersed tunnel can be obtained by
s
b
u
u
(6)
where
u
b
= displacement of tunnels; and
α
= ratio of soil
displacement at the base of the tunnel to that of soil particles.
The calculation method for
α
is not given in this paper due to
limitation of the space and the specific computational process
have been presented in detail in the related reference (Zhou,
1989).
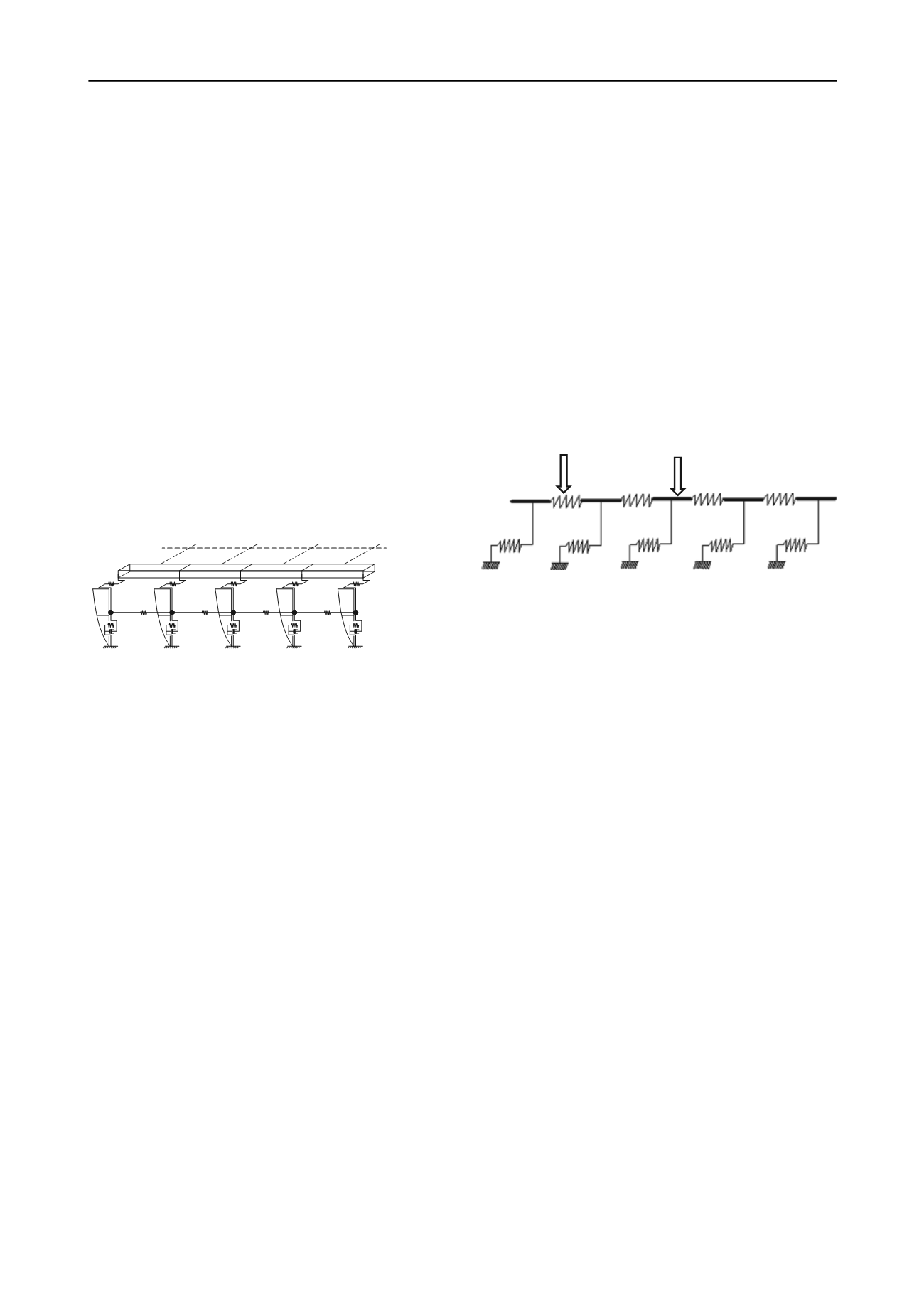
4 INTERNAL FORCE OF THE TUNNEL STRUCTURE
The tunnel structure is modeled as a Winkler elastic foundation
beam with joints, which is simplified into translational springs
to simulate the behavior of compressing and tension of GINA
gaskets under seismic loading (Fig. 3). The seismic response of
the tunnel is obtained by applying the seismic displacement of
free field to interaction springs between the tunnel and strata
without considering the inertia of the tunnel. The seismic
displacement of the tunnel can be obtained by
t
b
t
t
u uK uK
1
(7)
where
K
t
and
K
1
= stiffness matrix of the tunnel and interaction
spring, in which
K
1
is frequency-independent static stiffness;
u
t
= seismic response displacement of the tunnel.
Immersion joint
Segment
Figure 3. Simplified model of the immersed tunnel structure for response
displacement method
5 MODIFIED RESPONSE DISPLACEMENT METHOD
Based on the Fast Fourier Transformation (FFT) technique and
the theory of dynamic elastic Winkler foundation beam, a
modified response displacement method is presented in this
paper. Inertia of the immersed tunnel can be considered in this
method as well as the dependency of soil-tunnel interaction
parameters on the frequency of external seismic loading.
5.1
Seismic deformation of free field
According to FFT, Eq. (1) given in Session 2.1 is changed into
s
s
s
s
UK i
UM
) 21(
2
(8
)
g s
UM
2
where
U
s
(
ω
) and
U
g
(
ω
) = Fourier amplitude of particle and
input seismic displacements, respectively;
i
= the imaginary unit;
ξ
= frequency-independent hysteretic damping ratio of the soil;
and
ω
= external frequency of seismic loading. The response
displacement of soil particle
u
s
in the time domain can be
obtained by the inverse Fast Fourier Transformation (IFFT) of
U
s
(
ω
).
Likewise, eq. (6) can be changed into
s
b
U
U
(9)
where
U
b
(
ω
) = Fourier amplitude of the displacement of the soil
at the base of the tunnel. Accordingly, the seismic displacement
of the free-field soil at the base of the tunnel
u
b
in the time
domain can be obtained by IFFT of
U
b
(
ω
).
5.2
Internal force of the tunnel structure
Inertia of the tunnel and dependence of soil-tunnel interaction
parameters on external frequencies are taken into account in the
modified response displacement method. The tunnel structure is
discretized into a series of particles, which is combined with the
soil through interaction springs and dashpots (Fig. 4). In
addition, the form of external loading is the seismic acceleration


