1713
Technical Committee 204 /
Comité technique 204
0
20
40
60
80
(MPa)
0
100
200
300
(MPa)
=0.0
=0.3
=0.5
=1.0
=0.1
=0.8
Peak strength
Residual strength
=0.2
=0.4
=0.6
=0.7
=0.9
Figure 3. Schematic evaluation of the stress loss parameter by using the
post-peak form of the Hoek-Brown failure for the Test No.1
marble specimen
Table 2. Results of post-peak strength estimation for the Test No.1
marble specimen (stress unit: MPa)
Mechanical parameters
Confining
stress
(
3
)
c
R
c
b
m
R
b
m
s
a
Peak
-
0 94
-
6.0
-
1.0 0.5
64
0.05
89
5.7 1.0 0.5
32
0.30
66
4.2 1.0 0.5
Post-peak
16
0.48
-
49
-
3.1 1.0 0.5
8
0.70
28
1.8 1.0 0.5
4
0.80
19
1.2 1.0 0.5
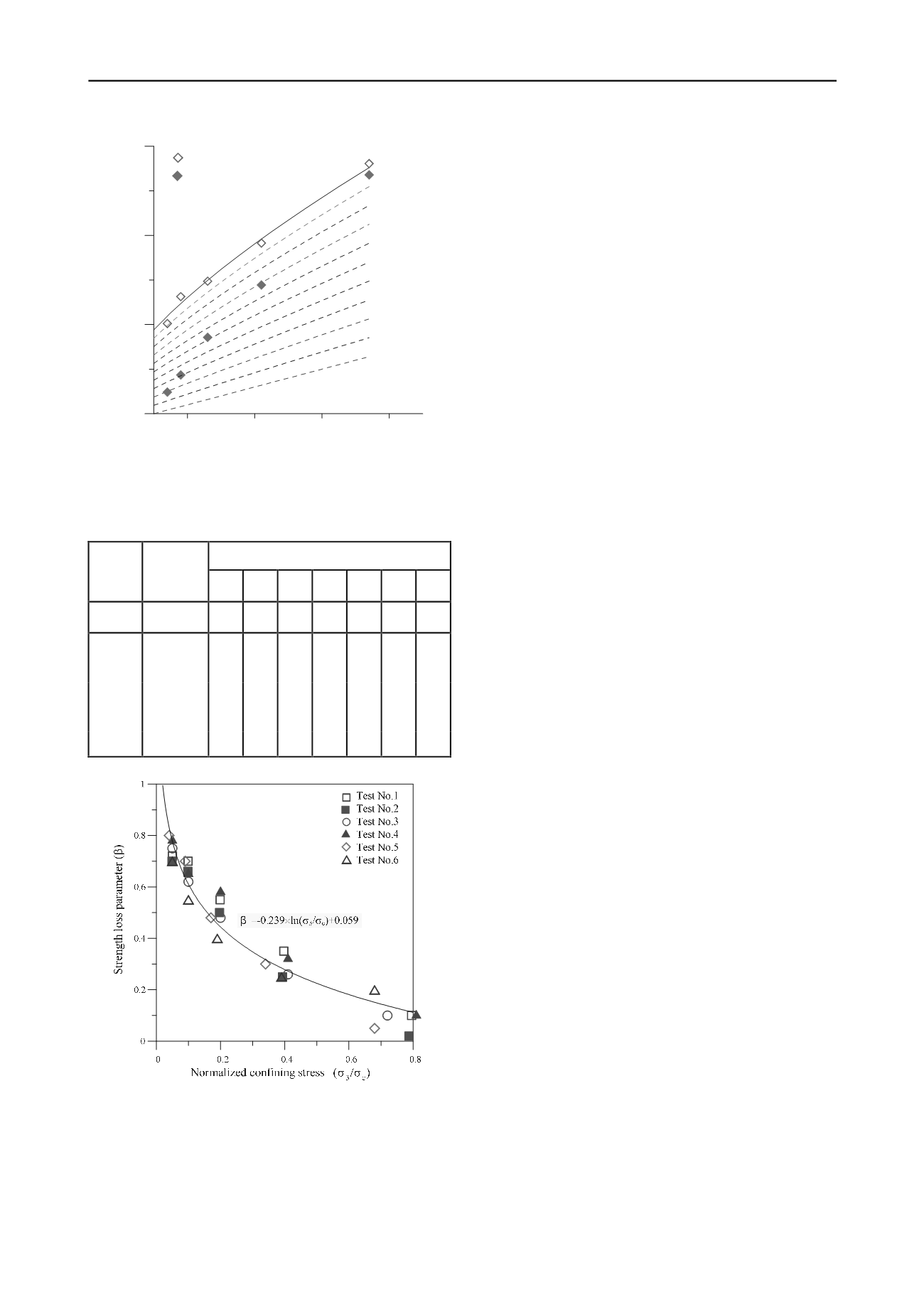
Figure 4. Correlation between strength loss parameter and normalized
confining stress on marble
Furthermore, the relationship between the strength loss
parameter and the normalized confining stress (divided by
uniaxial compressive stress) for the tests showed in Table 1 was
sketched (see Figure 4). From the figure, the strength loss
parameter is progressively increased with the decreasing of the
confining stress and the regression equation can be obtained as
059 .0 /
ln 239 .0
3
c
(5)
4 CASE STUDY
The effect of post-peak strength degradation on deep
underground excavation was examined by a modeling of a road
tunnel. The tunnel is part of the project providing a safe and
reliable connecting highway for east and north Taiwan. The
case tunnel is a twin-hole tunnel with excavation span of 12.5 m.
The pillar width between two tunnels is about 30 m. According
to the geotechnical survey report (Sinotech 2011), the main rock
type along the tunnel is marble, which average uniaxial
compressive strength is around 80 MPa. The strength
parameters of rock mass in good quality range (GSI=80) was
estimated by using the method suggested by Hoek (2002). The
estimation results of peak strength are listed in Table 3.
Furthermore, Equation 2, 3 and 5 was adopted to estimate the
post-peak strength under various confining stresses. The
computer program FLAC was used to simulate the tunnel
construction. A subroutine of FISH language embedded within
FLAC was developed to input the parameters of post-peak
strength depending on the value of confining stress as the
element is yielding during period of calculation.
The top heading method is designed for the tunnel
excavation and the cycle length is 3.5 m for good rock mass
(GSI=80). The support works used including 8 cm thick steel
fiber reinforced shotcrete with systematic rock bolts. The rock
bolts installed are of 25 mm
with length of 4 m and spaced of
2.0m
×
3.0~4.0m. The allowable tunnel deformation is 5 cm in
the support system. Two different overburden depths of 500 m
and 1000 m were considered in the case study. Vertical stress
(P
0
) was calculated by dead weight of rock mass as P
0
=
H,
where
is the unit weight of rock mass and H is the overburden
depth. The horizontal stress was estimated with references to the
results of in-situ overcoring test in the eastern Taiwan (Hsiao et
al. 2006). The maximum horizontal stress is 1.2 times of
vertical stress.
The Hoek-Brown model (no strength degradation, HB model)
and the post-peak strength degradation model (SD model) were
adopted to analyze the tunnel excavation behavior. The results
of the analyses are displayed in Table 4. When the overburden
depth is 500 m with the Hoek-Brown model, the roof settlement
of tunnel is 1.7 cm, the horizontal convergence of bench is 1.9
cm and both the relaxation zone thickness at the roof and the
sidewall are 0.5 m. Then the tunnel deformation would increase
apparently where the overburden reaches to 1000 m, that is, 3.8
cm in the roof settlement and 4.2 cm in the horizontal
convergence. And the relaxation zone thickness surrounding the
tunnel would increase to 1.5 m as well. However, the tunnel
deformation is still under the designed allowable value of 5 cm
even the tunnel depth reaches to 1000 m.
In case the post-peak strength degradation is considered, the
roof settlement of 3.7 cm and the horizontal convergence of
bench of 4.4 cm are obtained at the tunnel depth of 500 m in the
SD model. And approximate 2.6 times of deformation increased
would occur when the tunnel depth reaches to 1000 m, that is,
9.8 cm in roof settlement and 9.0 cm in horizontal convergence.
The tunnel deformation obviously exceeds the designed
allowable value and tunnel may need re-mining in deep
overburden condition, as shown in Figure 5.
The above analyses demonstrate that the characteristic of
post-peak strength degradation may affect the tunnel behavior.
The effect intensity is progressively significant with increasing
tunnel depth, as illustrated in Figure 5. There is an outstanding
increase in tunnel deformation at the depth of 1000 m for the
SD model. In case additional reinforcement or modified
excavation measure is not adopted, severe tunnel deformation
may endanger tunnel stability. The strength degradation of
marble beyond brittle failure plays an important role in the
stability of deep tunneling.


