1628
Proceedings of the 18
th
International Conference on Soil Mechanics and Geotechnical Engineering, Paris 2013
;
0
BB B
t
t
,
0
EE E
t
t
(4)
their relationship can be easily written as
,
0
0
B
E
K
B
E
t
t
t
(5)
where K
t
is the coefficient of the time variation of the
relationship between the base and foundation stiffness,
depending on the creep leak rate in the foundation and base, on
the level of their stress state, load duration etc.
0
40
80
120
160
1
2
3
3.5
Base
Foundation
t, days
t
Figure 1 – Chart of time behavior of creep properties of base soil
and foundation concrete
If, for example, the mean stress in the soil for the foundation
under consideration is assumed to be equal to σ=0,2МPа, a
different time behavior of K
t
will be obtained for all three
processes of loading the «base-foundation» system under
consideration (See Figure 2).
0
20
40
60
80
100
t, days
1
0.6
0.2
1.4
1.8
2.2
K
t
t
êð
K
t
min
Base soil and foundation concrete creep
Base soil creep
Foundation concrete creep
Figure 2 – Coefficient of base stiffness–to-foundation stiffness
relation time variation.
It is easy to note that K
t
≥1 grows over time with
development of the foundation material creep, with the base
creep manifestation (consolidation), K
t
≤1 – decreases, and at
simultaneous manifestation of rheological properties of the
foundation and base, there is a certain critical loading time tcr,
corresponding to the minimum value K
t
=K
tmin
. Consequently,
the moment of sustained loading, corresponding to the critical
time t= t
cr
may turn out to be the worst in terms of force
distribution in the system.
2 FOUNDATIONS SETTLEMENT UNDER DYNAMIC
LOADS
The dynamic loads caused by machinery operation can lead to
weak decaying machinery foundations settlements which can
often be quite substantial and uneven.
The available observational and experimental data obtained
while facilities were being subjected to dynamic loads indicate
that such settlements can cause buildings and structures
damages and the machines involved in the same technological
process dysfunction (Aleksandrovych 2012).
2.1
Foundation settlement forecast using heritable creep
theory
Soil massif provided with linearity in the dynamic tasks and its
rheological properties are estimated from the solution of energy
balance equation or heritable mechanics of deformable bodies.
The second case is considered in the paper. According to
Volterra`s approach, who interprets operators as constants, the
solution consists in a form of elastic constants and coordinates
function multiplication by function of time. Relying on known
Schleicher’s solution, the relation of stamp settling on linearly
elastic heritable half-space under fixed constant load is
presented in the following way:
t
ст
d tK
Е
b tS
0
2
)
(
1 )
1(
)(
,
(6)
where
)
(
tK
– is a creep kernel (Khain 1977, Savinov
1979).
According to Boltzmann, who was the first to formulate the
principle of inheritance, the kernel is used in the following way:
)
(
)
(
t
c
tK
(7)
Boltzmann kernel application results in the logarithmical
increase of the settlement with time (Rabotnov 1977). Under the
constant strain the finite expression reflecting the settlement
progressing with time equates as follows:
c t
tS
) ln(
)(
(8)
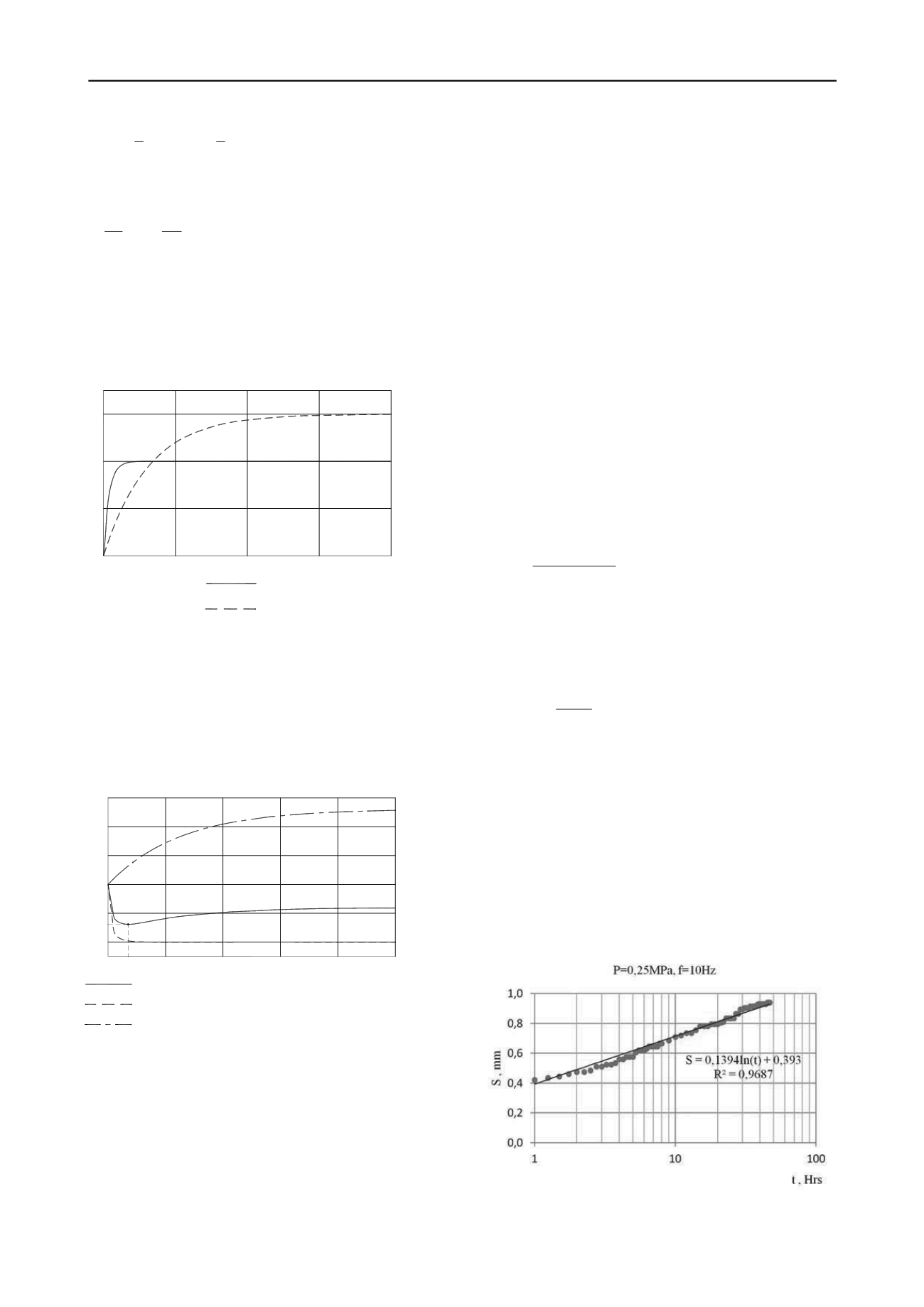
Data obtained from special vibrostamp experimental tests
conducted in compliance with the technique specified in
(Ilyichev at al. 1986) validate the expression competence to
describe the deformation progress with time on steady-state
(exhaustion) phase of creep (see figures 3 & 4).
Figure 3. The curve of settlement progress with time a
z
= 5µm.


