1653
Technical Committee 203 /
Comité technique 203
Proceedings of the 18
th
International Conference on Soil Mechanics and Geotechnical Engineering, Paris 2013
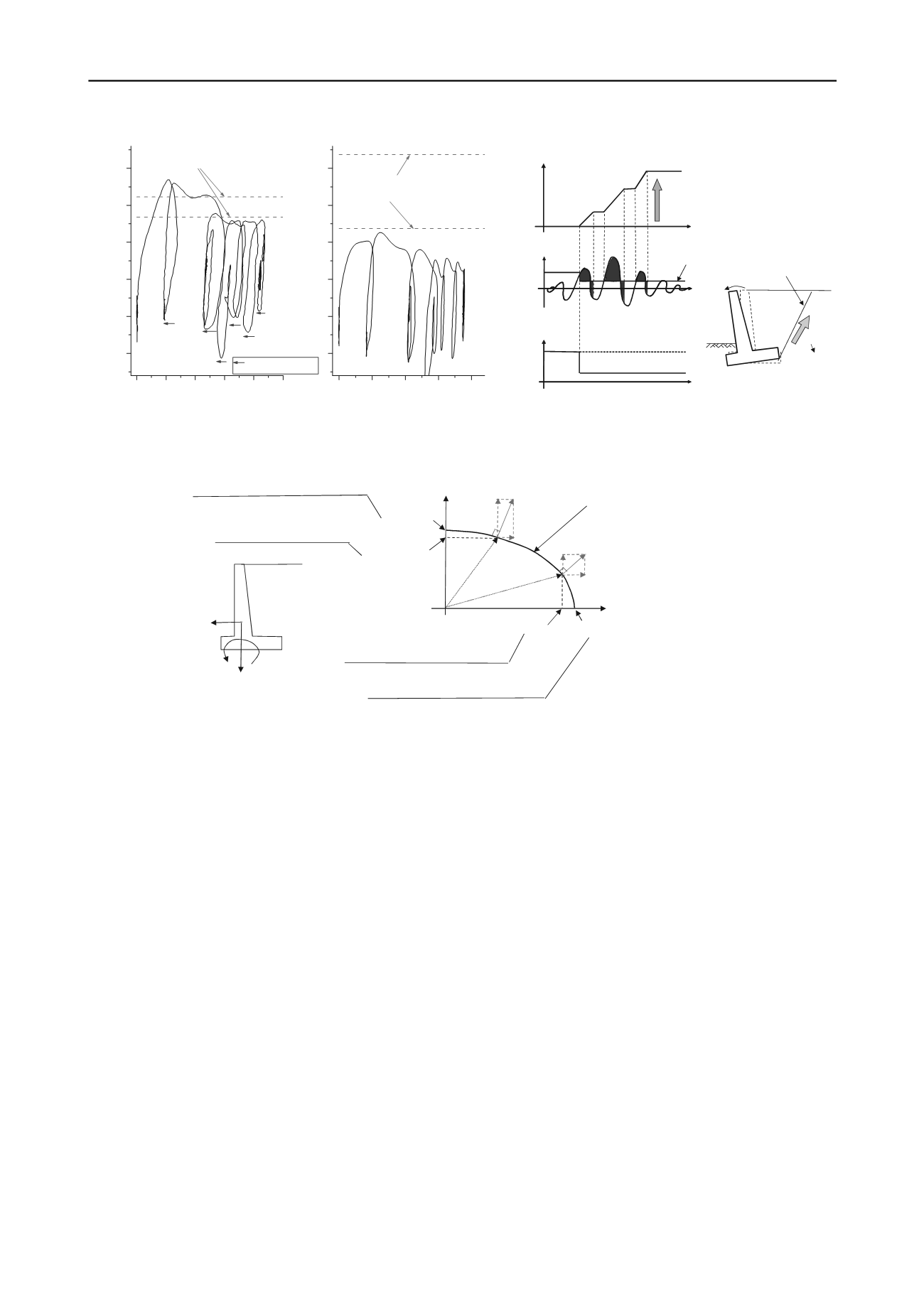
force reaches the maximum value. This maximum value has
been identified as being generally consistent with the maximum
resistance moment (M
md
) and the maximum horizontal bearing
capacity (R
hd
) of a retaining wall as shown in Figure 5 (see
below for detail). On the other hand, recovery of displacement
(elastic behavior) was small when the external forces were
applied in the backward direction (passive direction). It can be
said that the displacement increment of the retaining wall to the
active direction is largely affected by seismic ground motion
characteristics (duration and number of seismic motions).
3 A NEW METHOD TO EVALUATE THE RESIDUAL
DISPLACEMENT OF RETAINING STRUCTURES.
3.1
4B
Retaining wall
Based on the test results, a seismic design method using the
Newmark method (Newmark, 1965) was proposed for the
retaining wall (Figure 6).
The Newmark method has various advantages in that (1) the
theory is very simple and has very few analytical parameters
while still providing an adequate result; (2) seismic ground
motion characteristics can be directly considered, and (3) the
strength characteristics and strain softening behavior of the
backfill soil can be taken into account.
According to experience gained in the wake of past disasters
and model experiment results, overturning modes (rotational
mode) are common in the seismic response of retaining wall
foundations. Therefore, the Newmark method is indicated as
the method for calculating the response rotational angle of a
retaining wall in the new design standard. However since a
considerable eccentricity/inclined load at the base footing is
often caused by seismic earth pressure, this effect should be
considered when calculating the maximum resistance moment
(M
md
’
in Figure 7) of the foundation.
Furthermore, an
overturning mode does not necessarily occur independently but
can also be simultaneously accompanied by a sliding mode
when a spread foundation-type retaining wall has a low center
of gravity or when the passive resistance force at the front side
of base footing is small.
However, such failure mode
combinations cannot be taken into direct consideration since the
Newmark method uses a different motion equation for sliding
modes and overturning modes. Therefore, the combination of a
sliding mode and an overturning mode is determined if the
horizontal external force exceeds an horizontal stability level
when the response of the retaining wall reaches the maximum.
The displacement caused by the major failure mode is
calculated by the Newmark method and the displacement
caused by the minor failure mode is calculated from the yield
surface of the bearing capacity considering the associated flow
rule (Figure 7).
3.2
5B
Bridge abutment
Although the details of a study for bridge abutments have
been omitted due to space limitations in this paper, the effect of
inertial force and dynamic amplification was significant for
bridge abutments (Nishioka et al, 2011). This is because the
bridge abutment sustains the heavy bridge girder at the top.
This dynamic response characteristic is similar to that of a
bridge pier. In view of the above, a seismic design method was
proposed, which models the bridge abutment as a single-degree-
of-freedom system. This design method is almost similar to
bridge pier, however, seismic earth pressure acting on the
backface of bridge abutment is also considered.
0.00 0.01 0.02 0.03 0.04 0.05
0.00
0.05
0.10
0.15
0.20
0.25
of rotational angle
:slight elastic recovery
overturning mode
sliding and
overturing mode
Calculated maximum
resistance moment(M
md
)
Overturning moment(kN m/m)
Response rotational angle(rad)
0 5 10 15 20
0.0
0.5
1.0
1.5
2.0
2.5
a)
b)
overturning mode
sliding and
sliding mode
maximum horizontal
bearing capacity(R
hd
)
Horizontal external force(kN/m)
Horizontal displacment
at the bottom(mm)
Figure 5 Relationship between overturning moment (external
Figure 6 Newmark method for retaining wall (overturning mode)
force) and response rotational angle (horizontal displacement)
H
M
H
M
V
M
md
′
H
max
H
max
′
M
md
Maximum resistance moment
(overturning mode)
• •
=R
hb
• •
• •
=R
hb
′
)
Yield surface of the
bearing capacity
<External force acting on foundation>
Bδθ
Displacement
increment vector
δh
δh
Bδθ
δh
:
Horizontal displacement increment
Bδθ
:
Rotational angle increment
(B
:
footing width)
Displacement
increment vector
Maximum resistance moment
(under the combination of sliding
and overturning mode)
Maximum horizontal bearing capacity
(sliding mode)
Maximum horizontal bearing capacity
(under the combination of sliding and
overturning mode)
Figure 7 Yield surface of bearing capacity and the associated flow rule
Moment, M
M
md
(threshold)
φ
peak
φ
res
Responserotational
angle(rad)
Time
Accumulation of
rotational angle
Mobilized internal
friction angle
Peak strength
Residualstrength
Failureplane
φ
peak
φ
res
Overturning
Time
Time


