1532
Proceedings of the 18
th
International Conference on Soil Mechanics and Geotechnical Engineering, Paris 2013
Figure 2. Augmentation du CRR par augmentation de la compacité
(
cf.
abaque guide AFPS 2012).
3 RÉDUCTION DES SOLLICITATIONS SISMIQUES
Le deuxième effet concerne la diminution de la contrainte de
cisaillement dans le sol (diminution du CSR), sous l’effet d’un
report de contraintes sur la colonne plus raide. Le massif de sol
renforcé présente ainsi une déformation de cisaillement plus
faible qui entraine une réduction du potentiel de liquéfaction.
De nombreuses études ont été effectuées sur le sujet mais
souvent en négligeant un des éléments primordiaux de la
modélisation des colonnes ballastées à savoir la mise en œuvre
par refoulement. Nguyen et al. 2007 montre que sans la prise en
compte de cette expansion de diamètre qui permet de modifier
le rapport des contraintes k =
σ
’
h
/
σ
’
v
, l’augmentation de la
rigidité du massif renforcé par colonnes ballastées est fortement
sous-estimée.
3.1 Non prise en compte de la mise en œuvre de la colonne
ballastée par refoulement
Rayamajhi et al. (2012) ont mené une étude aux éléments finis
en élastique linéaire destinée à déterminer l’efficacité des
inclusions non refoulantes (colonne de sol malaxé, colonne de
gravier, inclusion rigide) vis-à-vis de la réduction des
contraintes de cisaillement sismiques dans un profil de sols
liquéfiables. Les résultats de la modélisation d’une cellule
élémentaire comportant une inclusion et le sol environnant au
sein d’une maille montrent que la colonne se déforme en
cisaillement et en flexion (voir Figure 3) avec une
prédominance de la flexion sur les deux premiers mètres puis
ensuite de cisaillement. La réduction des sollicitations de
cisaillement dans le sol environnant de l’inclusion est croissante
avec la profondeur mais négligeable sur les deux premiers
mètres en raison de la flexion.
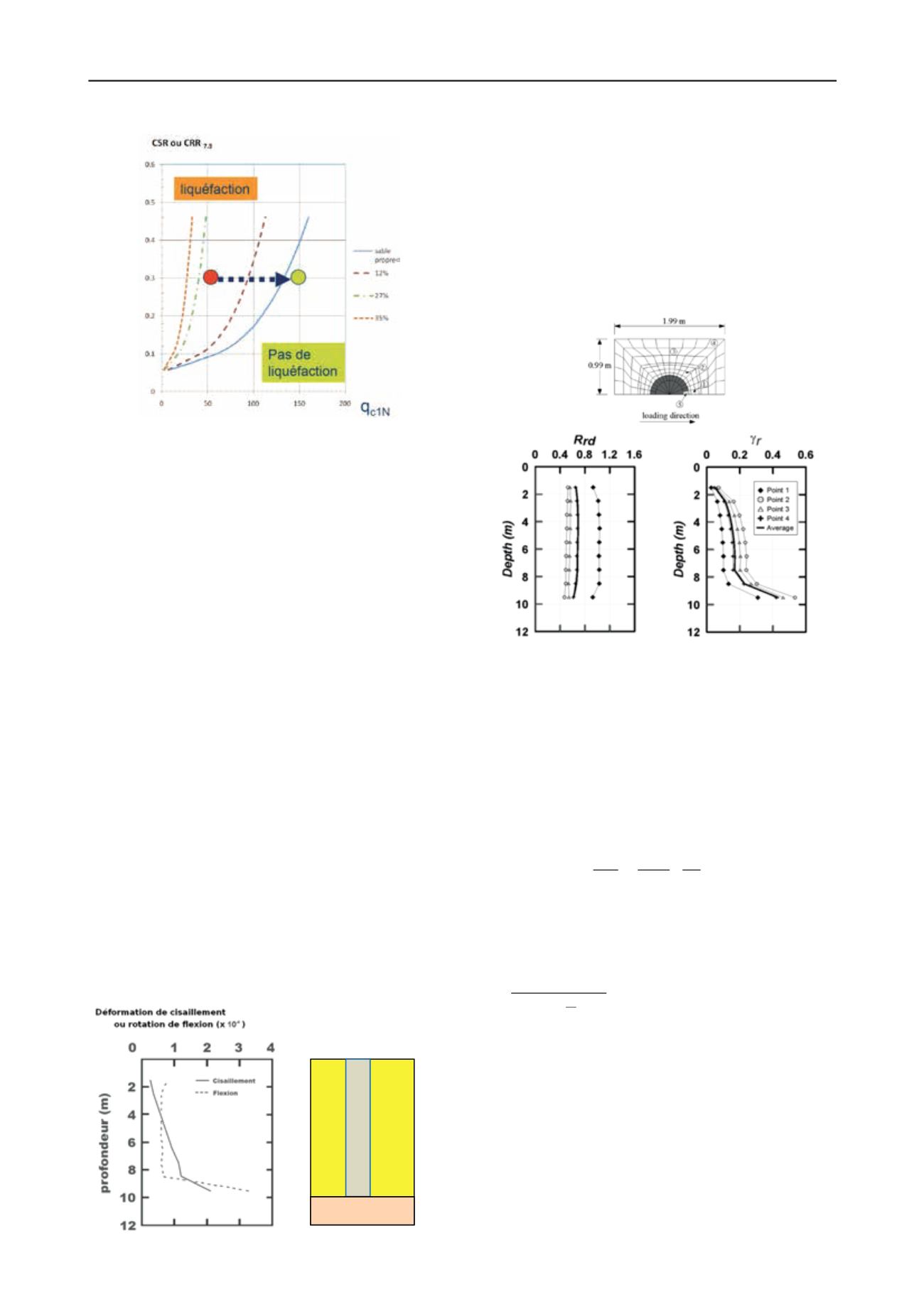
Figure 3. Déformation de cisaillement et de flexion d’une analyse
pseudo-statique Ar = 20 % et Gr = 10 (Rayamajhi et al. 2012).
Rayamajhi montre également que du fait de la non
homogénéité de la distorsion dans la maille élémentaire, une
diminution de la distorsion moyenne du volume renforcé
n’entraîne pas nécessairement une réduction de la distorsion
équivalente en tout point du sol. Sur la Figure 4, les profils de
γ
r
(rapport de la déformation de cisaillement de la colonne sur
celle du sol) pour cinq positions différentes en plan, sont
représentés en fonction de la profondeur. On peut constater que
la déformation de cisaillement est maximale dans la zone 1.
Figure 4. Distributions spatiales de R
rd
et
γ
r
obtenues à partir d’une
sollicitation sismique avec A
r
= 20 % et G
r
=10
(
Rayamajhi et al. 2012).
Les méthodes de dimensionnement qui supposent la
compatibilité des déformations de l’inclusion et du sol (
cf.
Baez
et Martin 1993) peuvent donc amener à surestimer la réduction
potentielle des contraintes de cisaillement liée à la présence
d’inclusion.
À partir de la méthode simplifiée de Seed et Idriss (1971)
pour la détermination du CSR, Rayamajhi propose de
déterminer l’augmentation du coefficient de sécurité du sol
renforcé en introduisant un coefficient de réduction de CSR
nommé R
CSR
tel que :
F
s final
= F
s initial
/ R
CSR
(1)
avec R
CSR
=
= (
,
,
).(
,
,
) = R
a max
. R
rd
u = sol non renforcé, i = sol renforcé,
r
d
coefficient de profondeur.
Rayamajhi et al. (2012) propose de modifier l’équation de Baez
et Martin (1993) de la manière suivante :
R
rd
=
.
(2)
où
C
G
: facteur équivalent de cisaillement de l’élément de
renforcement de sol qui dépend de sa géométrie (C
G
= 1
pour des éléments de renforcement circulaire),
G
r
: rapport du module de cisaillement de la colonne sur celui
du sol,
A
r
: taux de substitution soit A
col
/A
maille
,
γ
r
: rapport de déformation de cisaillement entre la colonne et la
déformation du sol environnant. Sur la base de plusieurs
études paramétriques pour des A
r
et G
r
différents, il peut
être estimé par
γ
r
= (G
r
)
-0,8
pour des modèles géométriques
basiques.
Sable compact
Sable
lâche
CB


