1529
Technical Committee 203 /
Comité technique 203
Après avoir installé la semelle sur le renforcement de sol, une
charge verticale de 5 000 N est appliquée progressivement en
cinq paliers réguliers. Cette charge est maintenue ensuite
constante pour assurer une complète consolidation du sol. La
charge verticale de 5 000 N correspond au tiers de la charge de
rupture du sol renforcé. Après la phase de consolidation du sol
sous la charge verticale, un chargement horizontal de 30 cycles
est appliqué sous déplacements contrôlés de +/- 2 mm à une
fréquence de 2,7 Hz.
Le macro capteur instrumenté mesure des déformations de
flexion à partir de 20 jauges. Les moments de flexion le long du
pieu ont été obtenus à partir de la loi de Hooke et de l’équation
de Euler-Bernoulli. La principale difficulté pour une telle
analyse est une interpolation temporelle correcte du moment sur
la hauteur de l’inclusion (Rosquoët et al. 2007). Ceci est
effectué avec une fonction polynomiale de degré 6 (Hana
Santruckova 2012).
3.3 Résultats des essais en laboratoire
3.3.1. Chargement vertical et horizontal
L’objectif est de trouver la combinaison des charges limites
verticale V et horizontale H qui provoque la rupture de la
fondation isolée.
Cette courbe enveloppe de rupture peut être trouvée
expérimentalement par une augmentation de la charge verticale
jusqu’à sa capacité ultime, puis en appliquant une force
horizontale tout en bloquant la fondation verticalement en
déplacement. Cette procédure est communément appelée le
« swipe test ». La mesure des forces verticales et horizontales
appliquées sur la fondation donne pour la semelle la courbe de
rupture du sol renforcé par Colonnes Mixtes.
Le « swipe test » a été effectué pour le sol non renforcé et le
sol renforcé par les Colonnes Mixtes. Un comparatif de ces 2
courbes (voir figure 5) met en évidence que la courbe de rupture
du sol renforcé est bien plus large que celle du sol non renforcé.
La forme de ces deux enveloppes est homothétique avec un
rapport approximatif de 4 entre les deux courbes.
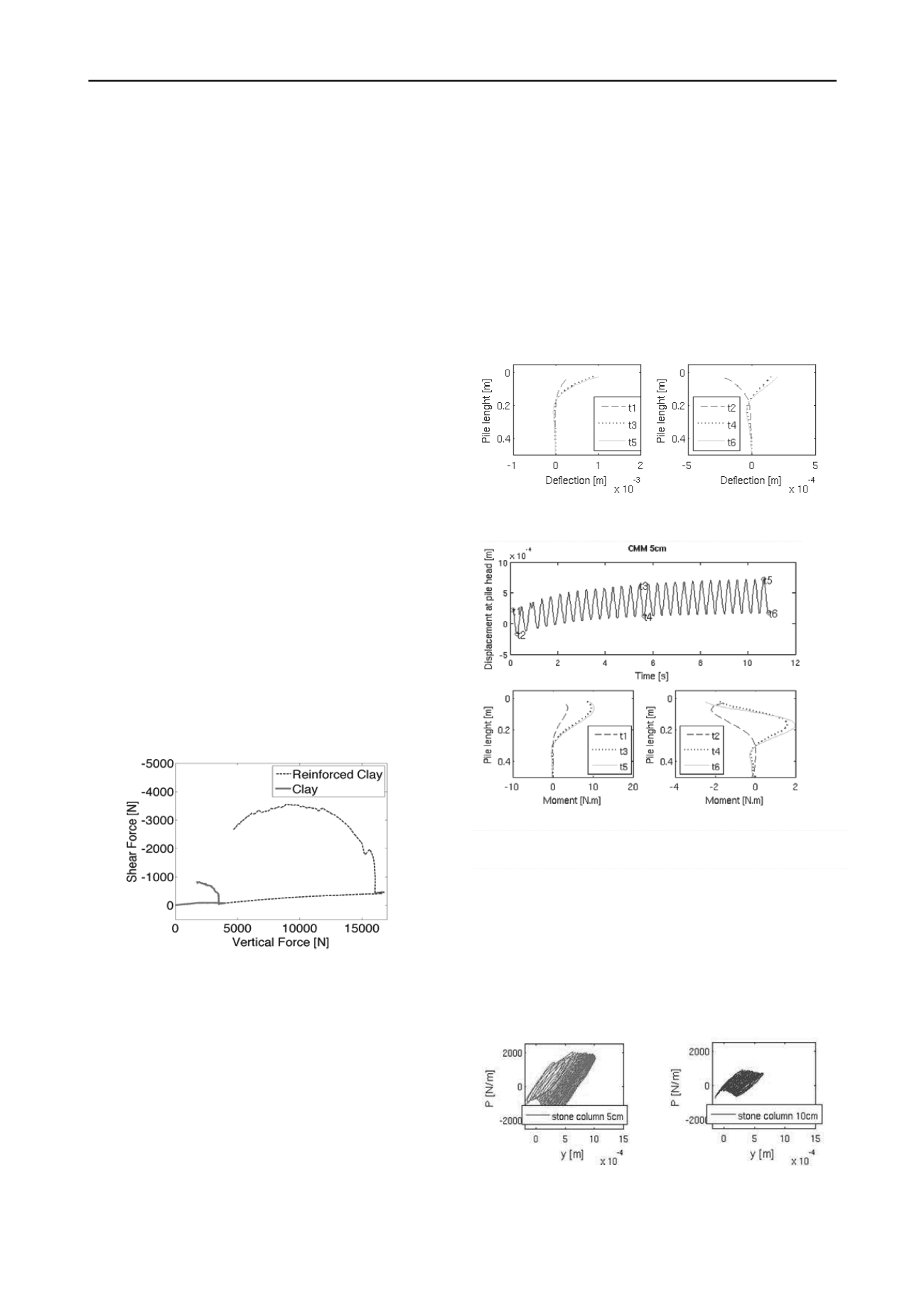
Figure 5. Swipe test pour le sol argileux non renforcé et le sol renforcé
avec Colonnes Mixtes
.
3.3.2. Chargement cyclique horizontal
La partie souple en gravier de la CMM
®
a pour intérêt principal
de dissiper au maximum l’énergie cinématique venant de la
fondation afin de réduire les sollicitations sur la partie rigide
constituée de mortier ou de béton. Dans le modèle physique
expérimental, il est apparu important d’étudier l’influence de la
hauteur de la partie souple (hauteurs variables de 5, 8 et 10 cm)
sur les sollicitations horizontales de la partie rigide sous-jacente.
La figure 6 montre ainsi que la tête de la partie rigide de la
Colonne Mixte se déplace horizontalement bien moins (0,2 mm
pour le premier cycle) que la fondation (+/- 2 mm) et que son
déplacement forme également une sinusoïde. Les courbes ont
été tracées pour les temps t1 à t6 correspondant aux premier,
quinzième et trentième cycles.
Sachant qu’une seule inclusion a été instrumentée, il est
possible de connaître les sollicitations des inclusions avant (sens
du déplacement) pour t1, t3 et t5 et les sollicitations des
inclusions arrière pour t2, t4 et t6 (voire Figures 6 et 7). On peut
constater que le moment de flexion en tête de l’inclusion rigide
n'a pas une valeur nulle comme c’est obligatoirement le cas
pour les Colonnes Mixtes. Ceci est dû à un moment parasite
provoqué par l’évasement du tube fixé en tête.
La figure 7 montre un déplacement réversible au début du
chargement puis, à mesure que le nombre de cycles augmente,
l’inclusion n’a plus un débattement négatif et montre une
accumulation des déplacements avec le chargement dynamique.
Ce déplacement latéral cumulé, tout en restant toujours
faible par rapport au déplacement de la semelle, se développe
vers l’extérieur de la fondation et a une tendance à se stabiliser
vers la fin du chargement cyclique.
Fig
ure 6. Profils de déplacements pour les temps t1 à t6 (hauteur partie
souple 5 cm).
Figure 7. Profils des moments pour les temps t1 à t6 (hauteur partie
souple 5 cm).
L’influence de la hauteur de la partie souple de la Colonne
Mixte sur les sollicitations mesurées dans la partie rigide est
caractérisée par la représentation du déplacement y de la tête de
la partie rigide en fonction de la pression latérale du sol p de la
figure 8. On peut constater que le déplacement est beaucoup
plus faible avec une hauteur de colonne de 10 cm (déplacement
maximum de 0,6 mm) qu’avec une hauteur de 5 cm
(déplacement maximum de 1,0 mm) et que par conséquent les
fortes épaisseurs sont à favoriser pour réduire les sollicitations
dans les inclusions rigides.
Figure 8. Courbes p-y en tête de la partie rigide pour 5 et 10 cm de
colonne de gravier.
avoir installé la semelle sur le renforcement de sol, une
verticale de 5 000 N est appliquée progressivement en
aliers réguliers. Cette charge est maintenue ensuite
te pour assurer une complète consolidation du sol. La
verticale de 5 000 N correspond au tiers de la charge de
du sol renforcé. Après la phase de consolidation du sol
charge verticale, un chargement horizontal de 30 cycles
liqué sous déplacements contrôlés de +/- 2 mm à une
ce de 2,7 Hz.
macro capteur instrumenté mesure des déformations de
à partir de 20 jauges. Les moments de flexion le long du
t été obtenus à partir de la loi de Hooke et de l’équation
ler-Bernoulli. La principale difficulté pour une telle
est une interpolation temporelle correcte du moment sur
teur de l’inclusion (Rosquoët et al. 2007). Ceci est
é avec une fonction polynomiale de degré 6 (Hana
kova 2012).
Résultats des essais en laboratoire
Chargement vertical et horizontal
ctif est de trouver la combinaison des charges limites
le V et horizontale H qui provoque la rupture de la
on isolée.
tte courbe enveloppe de rupture peut être trouvée
entalement par une augmentation de la charge verticale
sa capacité ultime, puis en appliquant une force
tale tout en bloquant la fondation verticalement en
ment. Cette procédure est communément appelée le
test ». La mesure des forces verticales et horizontales
ées sur la fondation donne pour la semelle la courbe de
du sol renforcé par Colonnes Mixtes.
« swipe test » a été effectué pour le sol non renforcé et le
forcé par les Colonnes Mixtes. Un comparatif de ces 2
s (voir figure 5) met en évidence que la courbe de rupture
renforcé est bien plus large que celle du sol non renforcé.
me de ces deux enveloppes est homothétique avec un
approximatif de 4 entre les deux courbes.
. Swipe test pour le sol argileux non renforcé et le sol renforcé
lonnes Mixtes
.
3.3.2. Chargement cyclique horizontal
ie souple en gravier de la CMM
®
a pour intérêt principal
iper au maximum l’énergie cinématique venant de la
on afin de réduire les sollicitations sur la partie rigide
uée de mortier ou de béton. Dans le modèle physique
ental, il est apparu important d’étudier l’influence de la
r de la partie souple (hauteurs variables de 5, 8 et 10 cm)
sollicitations horizontales de la partie rigide sous-jacente.
figure 6 montre ainsi que la tête de la partie rigide de la
e Mixte se déplace horizontalement bien moins (0,2 mm
premier cycle) que la fondation (+/- 2 mm) et que son
ment forme également une sinusoïde. Les courbes ont
ées pour les temps t1 à t6 correspondant aux premier,
me et trentième cycles.
hant qu’une seule inclusion a été instrumentée, il est
e de connaître les sollicitations des inclusions avant (sens
du déplacement) pour t1, t3 et t5 et les sollicitations des
inclusions arrière pour t2, t4 et t6 (voire Figures 6 et 7). On peut
constater que le moment de flexion en tête de l’inclusion rigide
n'a pas une valeur nulle comme c’est obligatoirement le cas
pour les Colonnes Mixtes. Ceci est dû à un moment parasite
provoqué par l’évasement du tube fixé en tête.
La figure 7 montre un déplacement réversible au début du
chargement puis, à mesure que le nombre de cycles augmente,
l’inclusion n’a plus un débattement négatif et montre une
accumulation des déplacements avec le chargement dynamique.
Ce déplacement latéral cumulé, tout en restant toujours
faible par rapport au déplacement de la semelle, se développe
vers l’extérieur de la fondation et a une tendance à se stabiliser
vers la fin du chargement cyclique.
Fig
ure 6. Profils de déplacements pour les temps t1 à t6 (hauteur partie
souple 5 cm).
Figure 7. Profils des moments pour les temps t1 à t6 (hauteur partie
souple 5 cm).
L’influence de la hauteur de la partie souple de la Colonne
Mixte sur les sollicitations mesurées dans la partie rigide est
caractérisée par la représentation du déplacement y de la tête de
la partie rigide en fonction de la pression latérale du sol p de la
figure 8. On peut constater que le déplacement est beaucoup
plus faible avec une hauteur de colonne de 10 cm (déplacement
maximum de 0,6 mm) qu’avec une hauteur de 5 cm
(déplacement maximum de 1,0 mm) et que par conséquent les
fortes épaisseurs sont à favoriser pour réduire les sollicitations
dans les inclusions rigides.
Figure 8. Courbes p-y en tête de la partie rigide pour 5 et 10 cm de
colonne d gravier.
Après avoir installé la semell sur le renforcement de sol, une
harge verticale de 5 000 N est appliquée progressiv ment en
cinq paliers réguliers. Cette charge est maintenue ensuite
constant pour assurer une mplète consolidation du sol. La
charge verticale de 5 000 N correspond au tiers de la charge de
rupture du sol renforcé. Après la phase de consolidation du sol
sous la charge verticale, un chargement horizontal de 30 cycles
est appliqué sous déplacements contrôlés de +/- 2 mm à une
fréquence de 2,7 Hz.
Le macro capteur instrumenté mesure es déf rmatio s e
fl xion à partir de 20 jauges. Les moments de flexion le long du
pieu ont été obtenus à partir de la loi de Hooke et de l’équation
de Euler-Bernoulli. L principale difficulté pour un telle
analyse est une interpolation temporelle correcte du moment sur
la ha teur de l’inclusion (Rosquoët et al. 2007). Ceci est
effect é avec une fonction polynomiale de degré 6 (Hana
Santruckova 2012).
3.3 Résultats des essais en laboratoire
3.3.1. Chargement vertical et horizontal
L’objectif est de trouver la combinaison des charges limites
verticale V et horizontale H qui provoque la rupture de la
fondation is lée.
Cett courbe enveloppe de rupture peut être trouvé
expérimentalement par une augmentation de la charge verticale
jusqu’à sa capacité ultime, puis en appliquant une force
horizontale tout en bl quant la fondatio verticalement en
déplacem nt. Cette procédure est communément appelée le
« swipe test ». La mesure des forces verticales t horizontales
appliquées sur la fondation don e pour la semelle la courbe de
rupture du sol renforcé par Colonnes Mixtes.
Le « swipe test » a été effectué pour le sol non renforcé et le
s l enforcé par les Colonnes Mixtes. Un comparatif de ces 2
courbes (voir figure 5) met en évidence qu la c urbe de rupture
du sol renforcé est bien plus large que celle du sol non renforcé.
La f rme de ces deux enveloppes est homothétique avec un
rapport approximatif de 4 entre les deux courbes.
Figure 5. Swipe tes pour le sol argileux non renforcé et le s l renforcé
avec Colonnes Mixtes
.
3.3.2. Chargement cyclique ho izontal
La part e souple en gravier de la CMM
®
a pour intérêt principal
de dissiper au maximum l’énergie cinématique venant de la
fonda ion afin de réduire les sollicitations sur la partie rigide
constituée de mor ier ou de béton. Dans le modè e physique
expérimental, il est apparu important d’étudier l’influence de la
haut ur de la partie souple (hauteurs variables de 5, 8 et 10 cm)
sur les sollicitations horizontales de la partie rigide sous-jacente.
La figure 6 montre ainsi que la tête de la partie rigide de la
Colonne Mixte se déplace horizont lement bien moins (0,2 mm
pour le premier cycle) que la fo dation (+/- 2 mm) et que son
déplacement forme également une sinusoïde. Les courbes ont
été tracées pour les t mps t1 à t6 correspondant aux premier,
quinzième et trentièm cycles.
Sachant qu’une s ule in lusi n a été instrumentée, il est
possible de connaître les sollicitations des inclusions avant (sens
du déplacement) pour t1, t3 et t5 et les sollicitations des
inclusions arrière p ur t2, t4 et t6 (voire Figures 6 et 7). On peut
constater que le moment de flexion en tête de l’inclusion rigide
n'a pas une valeur nulle comme c’est obligatoirement le cas
pour les Colonnes Mixtes. Ceci est dû à un moment parasite
provoqué par l’évasement du tube fixé en tête.
La figure 7 montre un déplacement réversible au début du
chargement puis, à mesure que le nombre de cycles augmente,
l’inclusion n’a plus un débattement négatif t montre ne
accumulation des dépl cements avec le chargement dynamiq e.
Ce déplacement latéral cumulé, tout en restant toujours
faible par rapport au déplacement de la semelle, se développe
l’extérieur de la fondation et a une tendance à se stabiliser
vers la fin du chargement cyclique.
Fig
ure 6. Profils de déplacements pour les temps t1 à t6 (hauteur partie
souple 5 cm).
Figur 7. Profils des moments pour les temps t1 à t6 (hauteur partie
souple 5 cm).
L’influence de la hauteur de la partie souple de la Colonne
Mixte sur les sollicitations mesurées dans la partie rigide est
caractérisée par la représentation du déplacement y de la tête de
la partie rigide n fonction de la pression latérale du sol p de la
figure 8. On pe t constate que le déplacement est beaucoup
plus faible av c une hauteur de colonne de 10 cm (déplacement
maximum de 0,6 mm) qu’avec une hauteur de 5 cm
(déplacement maximum de 1,0 mm) et que par conséquent les
fortes épaisseurs ont à favoriser pour réduire les sollicitations
dans les inclusions rigides.
Figure 8. Courb s p-y en tête de la partie rigide pour 5 et 10 cm de
colonne de gravier.
Après avoir installé la semelle sur le renforcement de sol, une
charg verticale de 5 000 N est appliquée progressivem nt en
cinq paliers réguli rs. Cette charge est maintenue ensuit
constante pour assurer une complète consolidation du sol. La
charge verticale de 5 000 N correspond u tiers de l charge de
rupture du sol renforcé. Après la phase de consolidation du sol
sous la ch rge v rticale, un chargement horizontal de 30 cycles
st appliqué sous déplacements contrôlés de +/- 2 mm à une
fréquence de 2,7 Hz.
Le macro capteur instrumenté mesure des déformations de
flexion à partir de 20 jauges. Les m ments de flexion le long u
pieu ont été obtenu à partir de la l i de Hooke et de l’équation
de Euler-Bernoulli. La principale d fficulté pour une telle
analyse est une interpolation temporelle correcte du moment sur
la hauteur de l’inclusion (Rosquoët et al. 2007). Ceci est
effectué avec une fonction polynomiale de degré 6 (Hana
Santruckova 2012).
3.3 Résultats des essais en laboratoire
3.3.1. Chargement vertical et horizontal
L’objec if est de trouver la combinaison des charges limites
rticale V et horizontale H qui provoque la rupture de la
fondation isolée.
Cette courbe enveloppe de rupture peut être trouvée
expérimentalement par une augmentation de la charge verticale
jusqu’à sa c pacité ultime, puis en appliquant une force
horizontale tout en bloquant la fondation verticalement en
déplacement. Cette procédure est communément appelée le
« swipe test ». La esure des forces verticales et horizontales
appliquées sur la fondation donne pour la semelle la courbe de
rupture du sol renforcé par Colonnes Mixtes.
Le « swipe test » a été effectué pour le sol non renforcé et le
sol r nforcé ar les Colon es Mixtes. Un comparatif de ces 2
courbes (voir figure 5) met en évid nce que la courbe de rupture
du sol renforcé st bien plus large que celle du sol non renforcé.
La forme de ces d ux enveloppes est homothétique avec un
rapport a roximatif de 4 entre les d ux courbes.
Figure 5. Swipe test pour le sol argileux non renforcé et le sol renforcé
avec Colonnes Mixtes
.
3.3.2. Chargement cyclique horizontal
La partie souple en gravier de la CMM
®
a pour intérêt principal
de dissiper au maximum l’ nergie cinématique venant de la
fondation afin de réduire les sollicitations sur la partie rigide
constituée de mortier ou de béton. Dans le modèle physique
expérimental, il est apparu important d’étudier l’influence de la
hauteur de la partie souple (hauteurs vari bles de 5, 8 et 10 cm)
sur les sollicitations horizontales de la partie rigide sous-jacente.
La figure 6 montre ainsi q e l tête de la partie rigide de la
Colonne Mixte se déplace horizontalement bien moins (0,2 mm
pour le premier cycle) que la fondation (+/- 2 mm) et que son
déplaceme t forme également une sinusoïde. Les courbes ont
été tracées pour les temps t1 à t6 correspondant aux premier,
quinzième et trentième cycles.
Sachant qu’une seule inclusion a été instrumentée, il est
possible de connaître les sollicitations des inclusions avant (sens
du déplacement) pour t1, t3 et t5 et les sollicitations des
inclusions arrière pour t2, t4 et t6 (voire Figures 6 et 7). On peut
constater que le moment de flexion en tê e de l’inclusion rigide
n'a pas une valeur nulle comme c’est obligatoirement le cas
pour les Colonnes M xtes. Ceci est dû à un moment parasite
provoqué par l’évasement du tube fixé en tête.
La figure 7 montr un déplacement réversible au début du
chargement puis, à m sure que le nombre de cycles augmente,
l’inclusion n’a plus un débattement négatif et montre une
accumula ion des d placements avec le chargement dynamique.
Ce déplacement latéral cumulé, tout en restant toujours
f ible par rapport au déplacement de la semelle, se développe
vers l’ xtérieur de la fondation et a une tendance à se stabiliser
vers la fin du charg ment cyclique.
Fig
ure 6. Profils de déplacements pour les temps t1 à t6 (hauteur partie
souple 5 cm).
Figure 7. Profils des moments pour les temps t1 à t6 (hauteur partie
souple 5 cm).
L’influen e de la hauteur de la partie souple de la Colonne
Mixte sur les sollicitations mesurées dans la partie rigide est
caractérisée par la représentation du déplacement y de la tête de
la partie rigide en fonction de la pression latérale du sol p de la
figure 8. On peut const t r que le éplacement est beaucoup
plus faible avec une hauteur de colonne de 10 cm (déplacement
maximum de 0,6 mm) qu’avec une hauteur de 5 cm
(déplacement maximum de 1,0 mm) et que par conséquent les
fortes épaisseurs sont à fav ri er pour réduire les sollicitations
dans les inclusions rigides.
Figure 8. Courbes p-y en tête de la partie rigide pour 5 et 10 cm de
colonne de gravier.
A avo r nstal
e su re f e en d s , e
er i le e 00 N
app iq
r
t en
i
i rs égu s.
c
ma tenue e ui e
nst
our a sure un comp èt o a i n u so . a
harge v t ca 0 co
er de
tu so r nf é. Apr s la p a ons lidation d sol
u l ha
,
est
l qué so
ement
t
e +/- 2
u
uenc 2,7 H .
L acr a u n r menté
é or ati de
ex
.
e i ng du
pi u ont été obte u
t r de la l
e de l’
o
e Eule -Bern ll . L pr nci ale dif cu é
une te l
aly t e nte pol t t m e le c re e m m
h u e
inclu i n ( squo et l. 00 .
i e t
fectué v u e onction ol nom
a u 20 .
.
s es a
. . . C em
L’object f st de trouver la co i so es h es
ite
r c t hori
l
i
oq a up ure e l
t n
ée.
c e
ut être t o v
expé im n ale ent par une ugm tati n e
i
u’
c acité l i e, pui
a
n u o ce
h riz nt le to en
a f
i er c l en
déplacem . C o e
m m n p e le
« s ip est ». L esu s for e vert cales t horizo t l s
ppli ué s su l
dat nne
r a se l la
rbe
r u s
a
es x .
L «
o renf rc r es ol nne i es. Un c p
c ur v r
év d e q a c
du so ren rcé est bi plu larg que c l e s l non ren orcé.
a form s d ux ve ppes est homothétique ec
p oxi
.
Fi re .
ip te t o le l
il ux non enfo c et le sol
c
ec Colonn s Mi t s
.
3.3. . h rg m
e h ontal
L p ie
p n g r d la M o nté ê
d diss p a ax m én rgie c néma que ven nt d l
f
t n a
i e
ati u la p ti
i
c st ué e mort er ou ton. D le
e h siqu
expér mental, i st pparu imp rta t
udi nfl e ce de a
haut r de l p r s l h uteurs variables e 5, 8 t m)
s l s
icita o h o ta de l r i
.
L fi u e 6
t e a ns ue a tête e la pa igide de la
C n e Mi te s déplace horizontaleme t bie m i (0,
ur le
ier c c e) que l
t +
et
dé
e t rm a nt u e s nus de. L s
s o
ét tracé s u le
,
ui i m t tr ntième yc e .
u e
l
u
, il e
po si e n aî re l s s llic at s de
ons ava t (sen
du dé l c e po r 1, t et 5
l
io d
,
.
co s a er qu l moment lex on en tête de l’in u ion r
n'a p s une vale l o c’e t o gat i
n c s
.
r l’
.
eme pu s,
ur q
b e
s
,
acc m lat o
d pl cements ave le cha gement n m q e.
éplacement téral cu , out en
n ouj rs
f b par rap u
aceme t la se l , e dév op
v rs l’ t eur de f at n et a ne
d h e c i e.
i
ur . ro il
l
t
l t
t t
t
ti
oupl c .
Fi
7. P ofil
t
l t
t t
t
ti
upl 5 c .
L’influenc e la hauteur de a
i
p
Mi te su es sol c ati ns m surées da
rigide est
c é ée par l repr s tati n du d placem t y d a tête de
l r e i id n o t
l
ol p d la
figur 8. On peu c tater qu e
eauc u
p f i l e e
t r co onne de 1
(dé a em
maximum de 0,6 mm) qu’avec une au e
cm
( épl c e t m i u 1,0 mm) et que par conséquent les
for es
ss u so à avo ser p r
d n e n o i i e .
Fi ur .
es
t t l
ti i i
t
c lonne de avier.


