1505
Technical Committee 203 /
Comité technique 203
generation occurred without any significant shear deformation
and the specimens tolerate the cyclic load to reach the r
u
= 0.8.
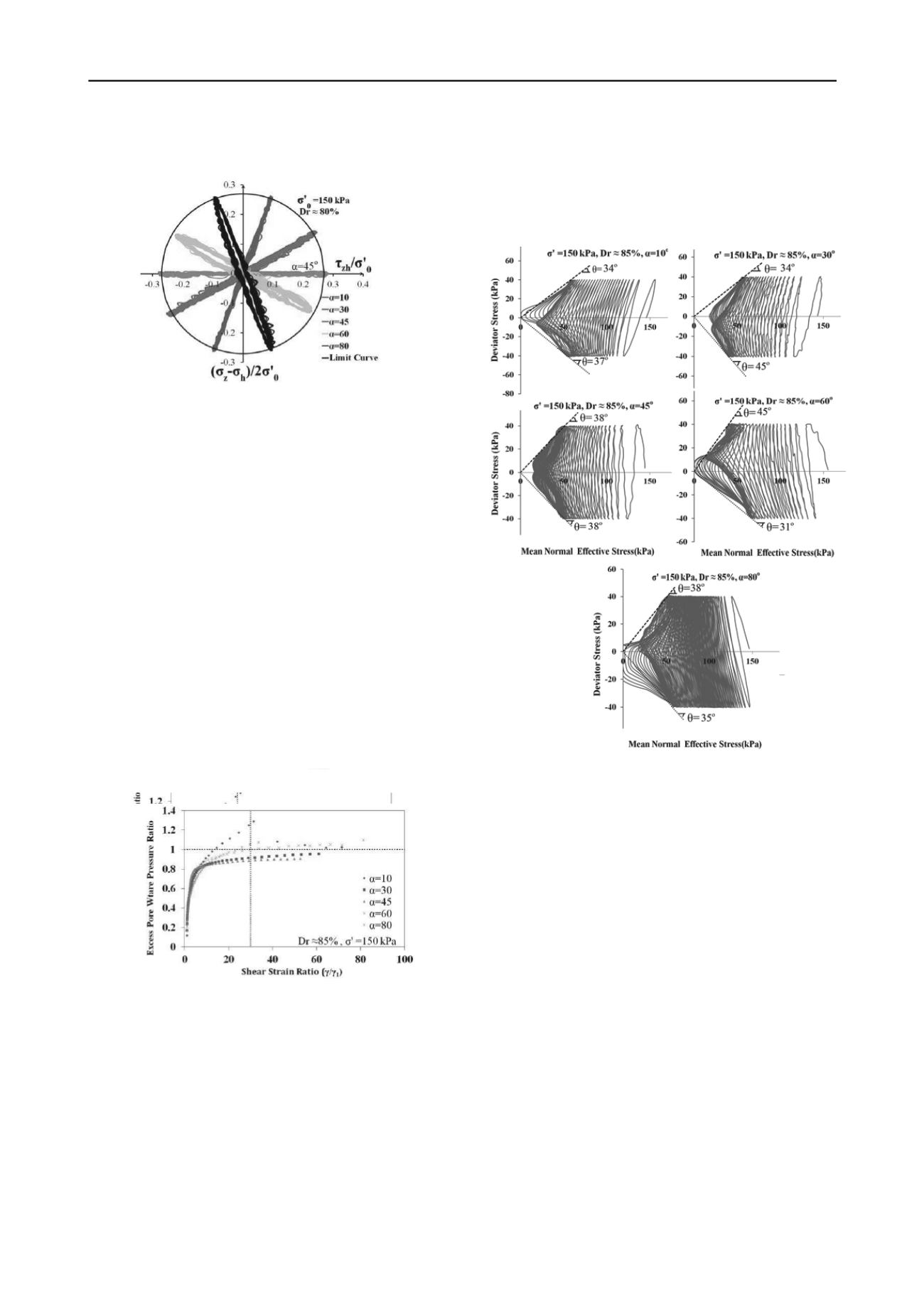
Figure 3. Stress paths of torsional shear stress and deviator in tests
In the second phase, by increasing of the pore water
pressure, the specimens lose their stiffness and show a higher
deformation more than ten times comparing to the first phase.
The third phase is the failure of the specimens, which is
accompanied with r ≈1.
u
Unlike other tests, the r
u
exceeded from 1 in the samples
tested at α=10 and 80 loading condition and their failure phase
occurred at γ/γ
1
of about 30 clearly. γ
1
is shear strain
corresponding to the first cycle. This cyclic response of
specimens is the result of the fact that tests were carried out in
stress controlled condition. At triaxial compression and
extension, the main part of the strain is result of axial and radial
strain and the shear portion of the strain is lesser. This kind of
deformation causes a brittle response of the specimens.
There are no separation in second and third phases of pore
water pressure generation trends in the samples tested at α=30,
45 and 60. The failure of these specimens is accompanied with
shear deformation. So the samples tested at α=30
o
, 45
o
and 60
o
show a softer response to the cyclic loads.
The stress path of deviator stress and mean normal effective
stress have been shown in Figure 5. As it shown in this figure,
the stress anisotropy has a great effect on stress path and the
cyclic responses of the same samples tested at different α.
Figure 4.Variation of excess pore water pressure ratio with shear strain
ratio
As it mentioned before, α and b were kept constant during a
test. So the reciprocal nature of cyclic loads would not change
the triaxial compression, triaxial extension or pure shear state of
the specimens. Therefore; the failure cover limits of a test were
related to the loading and reloading phase of the cyclic load.
With respect to the situation of sand particles, loading reversion
will change the sand particles interlock.
The sand particles interlock is very sensitive to the loading
direction as the slope of failure limit line would be changed at
different α, even during a load reversion phase.
Variations of strains in the first and fifteenth cycle of loading
are shown in Figure 6. Regarding to the nature of cyclic load, at
triaxial compression and extension tests, the axial strain (ε
z
) is
the major part of the specimens strain.
Because of the relative density of the specimens, the
expansive behavior is the expected response.
Figure 5.Stress paths of deviator and mean normal stress
At α=10
o
loading conditions the cyclic loading and reloading
had been imposed through the axial and radial load and the
specimens shows a vertical contractive responses to the cyclic
load, unlike the other tests. Expansive behavior of this test at
radial direction is result of its vertical contractive deformations.
The horizontal shear strains (ε
θ
) of the specimens are in the
similar trend, but their quantity reduces by approaching α to the
45
o
.
The pure shear nature of test at α=45
o
causes a higher
octahedral shear strains (γ
oct
). By increases and decreases of α
from 45
o
, γ
oct
would be decreased.
The variations of shear modulus and damping ratio of the
specimens have been shown in the Figures 7 and 8. The shear
modulus and damping ratio have been normalized with their
initial values. Results show that stress anisotropy had not
significant effect on stiffness reduction and damping ratio of the
dense specimens.
5 CONCLUSION
A series of undrained cyclic torsion shear tests on dense sand
samples using hollow cylinder apparatus were performed for the
purpose of investigating the effect of stress anisotropy on cyclic
behavior of Babolsar sand.
generation occurred without any significant shear deformation
and the specimens tolerate the cyclic load to reach the r
u
= 0.8.
Figure 3. Stress paths of torsional shear stress and deviator in tests
In the second phase, by increasing f the pore water
pressure, t e specimens lose their stiffness and ho a igher
deformation more than ten times comparing to the first phase.
The third phase is the failure of the specimens, which is
accompanied with r ≈1.
u
Unlike other tests, the r
u
ex eeded from 1 in the amples
tested at α=10 and 80 loading condition and their failure phase
occurred at γ/γ
1
of about 30 clearly. γ
1
is shear strain
corresponding to the first cycle. This cyclic response of
specimens is the result of the f ct that tests were c rried out in
stress controlled conditi n. At triaxial compression and
extensi , the main part of the strain is re ult of axial and radial
strain and the she r portio of the strain is lesser. This kind of
d formation causes a brittle respons of the specimens.
There ar no separation in s ond and third phases of pore
water pressure generation trends in the samples tested at α=30,
45 nd 60. The failure of these specimens is accompanied with
shear deform tion. So the samples tested t α=30
o
, 45
o
and 60
o
show a softer response to the cyclic loads.
The stre s path of deviator stress and mean normal effective
stress have been shown in Figure 5. As it shown in this figure,
the stress anisotropy has a great effect on stress path and the
cyclic responses of the same sam l tested at differ nt α.
Figure 4.Variation of excess pore water pressure ratio with shear strain
ratio
As it mentioned before, α and b were kept constant during a
test. So the reciprocal nature of cyclic loads would not change
the triaxial compression, triaxial extension or pure shear state of
the specimens. Therefore; the failure cover limits of a test were
related to the loading and reloading phase of the cyclic load.
With respect to the situation of sand particles, loading reversion
will change the sand particles interlock.
The sand particles interlock is very sensitive to the loading
direction as the slope of failure limit line would be changed at
different α, even during a load reversion phase.
Variations of str ins in the first and fift enth cycle of loading
are shown in Figure 6. Regarding to the nature of cyclic load, at
triaxial compression and xtension tests, the axial strain (ε
z
) is
the major part f the specimens strain.
Because of the relative density of the specimens, the
expansive behavior is the expected response.
Figure 5.Stress paths of deviator and mean normal stress
At α=10
o
loading conditi s the cyclic loading and reloading
had been imposed through the axial and radial load and the
specimens shows a vertical contractive responses to the cyclic
load, unlike the other tests. Expansive behavior of this test at
radial direction is result of its vertical contractive deformations.
The horizontal shear strains (ε
θ
) of the specimens are in the
similar tr nd, but their quantity reduces by approaching α to the
45
o
.
The pure shear nature of test at α=45
o
causes a higher
octahedral shear strains (γ
oct
). By increases and decreases of α
fro 45
o
, γ
oct
would be decreased.
The variations of shear modulus a d damping ratio of the
specimens have been
n in the Figures 7 and 8. The shear
modulus and damping ratio have been normalized with their
initial values. Results show that stress anisotropy had not
significant effect on stiffness reduction and damping ratio of the
dense specimens.
5 CONCLUSION
A series of undrained cyclic torsion shear tests on dense sand
s mples using hollow cylinder apparatus were performed for the
purpose of investigating the effect of stress anisotropy on cyclic
behavior of Babolsar sand.
Figure 3. Stress paths of torsional shear stress and deviator in tests
In the second phase, by increasing of the pore water
pressure, the specimens lose their stiffness and show a higher
deformation more than ten times comparing to the first phase.
The third phase is the failure of the specimens, which is
accompanied with r ≈1.
u
Unlike other tests, the r
u
exceeded from 1 in the samples
tested at α=10 and 80 loading condition and their failure phase
occurred at γ/γ
1
of about 30 clearly. γ
1
is shear strain
corresponding to the first cycle. This cyclic response of
specimens is the result of the fact that tests were carried out in
stress controlled condition. At triaxial compression and
extension, the main part of the strain is result of axial and radial
strain and the shear portion of the strain is lesser. This kind of
deformation causes a brittle response of the specimens.
There are no separation in second and third phases of pore
water pressure generation trends in the samples tested at α=30,
45 and 60. The failure of these specimens is accompanied with
shear deformation. So the samples tested at α=30
o
, 45
o
and 60
o
show a softer response to the cyclic loads.
The stress path of deviator stress and mean normal effective
stress have been shown in Figure 5. As it shown in this figure,
the stress anisotropy has a great effect on stress path and the
cyclic responses of t e same sampl s tested at differe t α.
Figure 4.Variation of excess pore water pressure ratio with shear strain
ratio
As it mentioned before, α and b were kept constant during a
test. So the reciprocal nature of cyclic loads would not change
the triaxial compression, triaxial extension or pure shear state of
the specimens. Therefore; the failure cover limits of a test were
related to the loading and reloading phase of the cyclic load.
With respect to the situation of sand particles, loading reversion
will change the sand particles interlock.
The sand particles interlock is very sensitive to the loading
direction as the slope of failure limit line would be changed at
different α, even during a load reversion phase.
Because of the relative density of the specimens, the
expansive behavior is the expected response.
Figure 5.Stress paths of deviator and mean normal stress
At α=10
o
loading conditions the cyclic loading and reloading
had been imposed through the axial and radial load and the
specimens shows a vertical contractive responses to the cyclic
load, unlike the other tests. Expansive behavior of this test at
radial direction is result of its vertical contractive deformations.
The horizontal shear strains (ε
θ
) of the specimens are in the
similar trend, but their quantity reduces by approaching α to the
45
o
.
The pure shear nature of test at α=45
o
causes a higher
octahedral shear strains (γ
oct
). By increases and decreases of α
from 45
o
, γ
oct
would be decreased.
The variations of shear modulus and damping ratio of the
specimens have been shown in the Figures 7 and 8. The shear
modulus and damping ratio have been normalized with their
initial values. Results show that stress anisotropy had not
significant effect on stiffness reduction and damping ratio of the
dense specimens.
5 CONCLUSION
A series of undrained cyclic torsion shear tests on dense sand
samples using hollow cylinder apparatus were performed for the
purpose of investigating the effect of stress anisotropy on cyclic
behavior of Babolsar sand.


