488
Proceedings of the 18
th
International Conference on Soil Mechanics and Geotechnical Engineering, Paris 2013
Proceedings of the 18
th
International Conference on Soil Mechanics and Geotechnical Engineering, Paris 2013
résultat par un calcul simple et fondé sur une connaissance la
plus parfaite possible de la loi contrainte-déformation de la
sollicitation pressiométrique du sol vierge. Dans ce sens, les
essais autoforés dans la plus large gamme de sols possible sont
une bonne réponse (Arsonnet et al., 2005), car ils permettent à
la fois la mesure du module initial G
0,
de la loi de décroissance
du module avec la contrainte (Baud & Gambin, 2005 ; Baud &
Gambin, 2008 ; Baud et al., 2012 et 2013), enfin l’évaluation du
coefficient
(Baud, 2005 ; Baud & Gambin, 2012).
2 PARAMETRES PRESSIOMETRIQUES NECESSAIRES
ET SUFFISANTS A LA DETERMINATION DE
.
2.1
Module E
M
, pression limite p*
LM
et confinement de
l’essai.
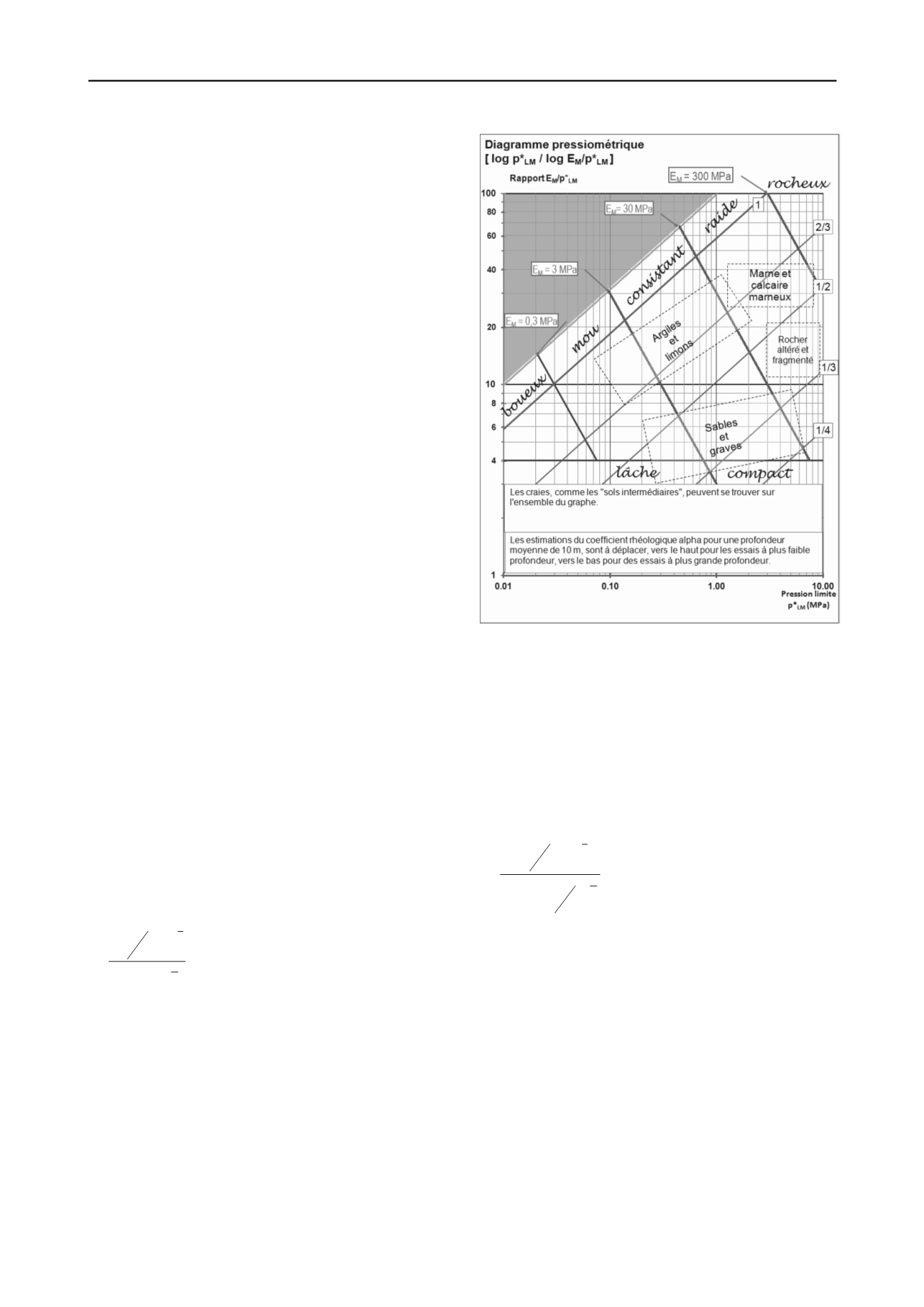
La première présentation du coefficient rhéologique
en
tableau à double entrée, en fonction du rapport E
M
/p*
LM
et de
l’état de consolidation du sol, qui avait été donnée dans la notice
D60 sur les « règles d’exploitation des techniques
pressiométriques et d’exploitation des résultats obtenus pur le
calcul des fondations » (Ménard, 1968) a été reconduite telle
quelle dans les règlementations françaises puis européennes.
Ménard prévoyait pourtant de réviser le tableau « en fonction de
résultats d’essais expérimentaux », raison principale pour
laquelle les valeurs de
étaient données sous forme de fractions
unitaires. Mais le principe était établi :
est croissant quand
E
M
/p*
LM
est croissant, depuis le comportement sableux jusqu’au
comportement argileux, et croissant également lorsque le sol
passe de la sous-consolidation ou de l’altération à la sur-
consolidation.
Pour suivre cette règle usuelle, des lignes d’isovaleurs des
valeurs fractionnaires de
peuvent être tracées directement
dans le diagramme bi-logarithmique Pressiorama® (Baud,
2005) en log (p*
LM
), log (E
M
/p*
LM
), tel qu’il a été édité en
annexe des normes NF P94-261 et NF P94-262 (Fig. 1), la
valeur 1 formant la limite supérieur du diagramme et la valeur
¼, la plus faible du tableau de Ménard, étant affectée au
rapports E
M
/p*
LM
très faibles, correspondant soit à des sables et
graviers, soit à des sols très remaniés, remaniement naturel in
situ, ou bien lié à une mauvaise exécution du forage
pressiométrique.
La principale raison de tracer des droites en coordonnées bi-
logarithmiques, était que l’on ne dispose absolument pas, dans
le référentiel des confrontations entre méthode pressiométrique
et fondations instrumentées, de données suffisantes pour
proposer des courbes plus sophistiquées. Ces droites sont donc
des constructions mathématiques simples, basée sur
l’hypothèse :
n
m
n
k
LM
LM
M
*p .
*p
E
1
(1)
Sous cette forme en effet, les coefficients m et n (en
exposants) et le facteur k, tous sans dimensions prennent
empiriquement les valeurs nécessaires pour assurer le tracé
désiré : m détermine l’angle des droites iso-
, n détermine
l’écartement entre les valeurs, et k détermine, pour un couple de
valeurs (m, n) donné, la position de la ligne maximale
= 1.
Les valeurs de
ainsi proposées peuvent être rendues assez
conformes au tableau à double entrée de Ménard pour des essais
à profondeur moyenne de quelques mètres utilisés pour des
fondations superficielles.
Mais on voit assez vite que si les valeurs de E
M
/p*
LM
décrivent toujours assez bien la nature du sol, sableux,
intermédiaire ou argileux, qui peut être connu par ailleurs au
moment du forage pressiométrique ou, mieux par un sondage
Figure 1 Valeurs de
dans le diagramme Pressiorama® tel qu’il peut
apparaître dans les normes NF-P94-261 et NF-P94-262 (en projet).
carotté au voisinage, la position des lignes d’isovaleurs de
par
rapport à p*
LM
n’est plus compatible dès lors que l’on considère
des essais réalisés à des profondeurs importantes : ceci est lié au
fait que ce n’est pas la valeurs absolue de p*
LM
qui doit être
prise en compte, mais la valeur relative p*
LM
/p
0
, sans
dimension, qui tient compte du confinement de l’essai par la
pression horizontale des terres au niveau où elle est mesurée.
On est ainsi conduit à la formulation suivante, dans laquelle
k
E
, m et n jouent le même rôle.
n
m
E
n
k
0
LM
LM
M
p
*p .
*p
E
1
(2)
Le nouveau diagramme [log (p* /p
0
), log (E
M
/p*
LM
)] qui en
itue une présentation peu
intuitive, essentiellement parce que le géotechnicien est très
habitué à ce que représente la pression limite, directement
proportionnelle à la résistance du sol, alors que la grandeur sans
dimension p*
LM
/p
0
est difficile à saisir. Elle représente en
quelque sorte le degré de résistance du sol soumis à l’essai par
rapport à une augmentation « normale » de résistance attendue
croissante en fonction de la profondeur.
LM
résulte n’est pas tracé ici. Il const
Les coefficients m et n peuvent prendre en théorie une large
gamme de valeurs, mais en pratique seule une faible gamme de
variations laisse les droites représentatives toutes présentes et
étalées dans le champ de vision du diagramme. Nous proposons
de les arrêter à m=0,5 et n=2, et avec ce couple de coefficients,
k
E
prendra une valeur comprise entre 3 et 5 pour que
reste
compatible avec l’usage. Nous avons retenu ici la valeur entière
k
E
=4, d’où :


