421
Technical Committee 101 - Session II /
Comité technique 101 - Session II
where
is non-symmetric tangential stiffness matrix at
, and the right term is residual load vectors.
), (
in
K
), (
in
t
3. MECHANICAL CONSTITUTIVE MODEL
The proposing mechanical constitutive model is based on the
following assumptions to define deformation characteristics
associated with THM phenomena.
First, the void of soils is fully saturated with water or
water/ice. That is, ice and unfrozen water fill the pore under
frozen condition, and the void is fully saturated with liquid water
above freezing temperature.
Second, porous material consisted of soil particles, water, and
ice is under local thermal equilibrium conditions
Based on these assumptions, this study proposes a mechanical
constitutive model for two-phase porous materials, with a similar
framework of BBM (Barcelona Basic Model) for unsaturated
soils (Alonso, et al. 1990). Stress and strain are positive value for
compression.
3.2. Stress variables
Mechanical constitutive law to describe deformational
behavior can be expressed by various stress variables. In
saturated soils, only effective stress is a stress variable to
determine soil behavior (Terzaghi, 1936). However, selection of
stress variables in unsaturated soils is still critical issue (Shin,
2011). The most previous studies for frozen soils performed TH
coupled analysis so that alteration of hydraulic and thermal
properties from deformation cannot be considered, or performed
simple linear-elastic analyses for frozen soil. Recently,
Nishimura et al. (2009) used net stress
and
suction
to simulate nonlinear deformation
behavior of frozen ground. However, ice pressure
below
freezing temperature shows such a rapid increase that it could be
greater than the sum of surface loads, soil skeletal force and
water pressure. These stress variables can lose physical meaning
and become discontinuous across freezing temperature, and it
inhibits numerical stability, along with emission of latent heat of
fusion.
) ,
max(
i l
n
PP p p
i
P
)0,
max(
l
i
PP s
In the developed model, a new stress variable
~
defines the
sum of soil skeletal stress and ice stress in Eq. (9), and internal
variable suction
s
(difference between ice pressure and fluid
pressure) only affect the pre-consolidation stress.
~
~
~
~ ~
1
1 ) 1(
l
l
i
P
P P
(9)
where
is total stress,
is effective stress
carrying soil skeletal force,
is ice pressure from
Clausius-Clapeyron equation, and is fluid pressure.
is
Kronecker’s delta tensor, and
)3,1 ,(
~
ji
ij
~
i
P
l
P
ij
~
1
is Bishop’s coefficient of
effective stress which can be simplified to degree of liquid water
saturation. The new stress variable
]1
~
) 1(
[
i
P
~
~
is the
same as effective stress above the freezing temperature. It can be
useful stress variable to develop mechanical constitutive model
for unsaturated freezing soils including air and gas phase.
3.3. Yield surface and plastic potential function
New stress variable
~
is used to define yield surface and
plastic potential function which describe deformational behavior
of frozen and unfrozen soils. The proposed yield function is
based on MCC (Modified Cam Clay) model which has an oval
shape of yield surface, taking account of bonding strength due to
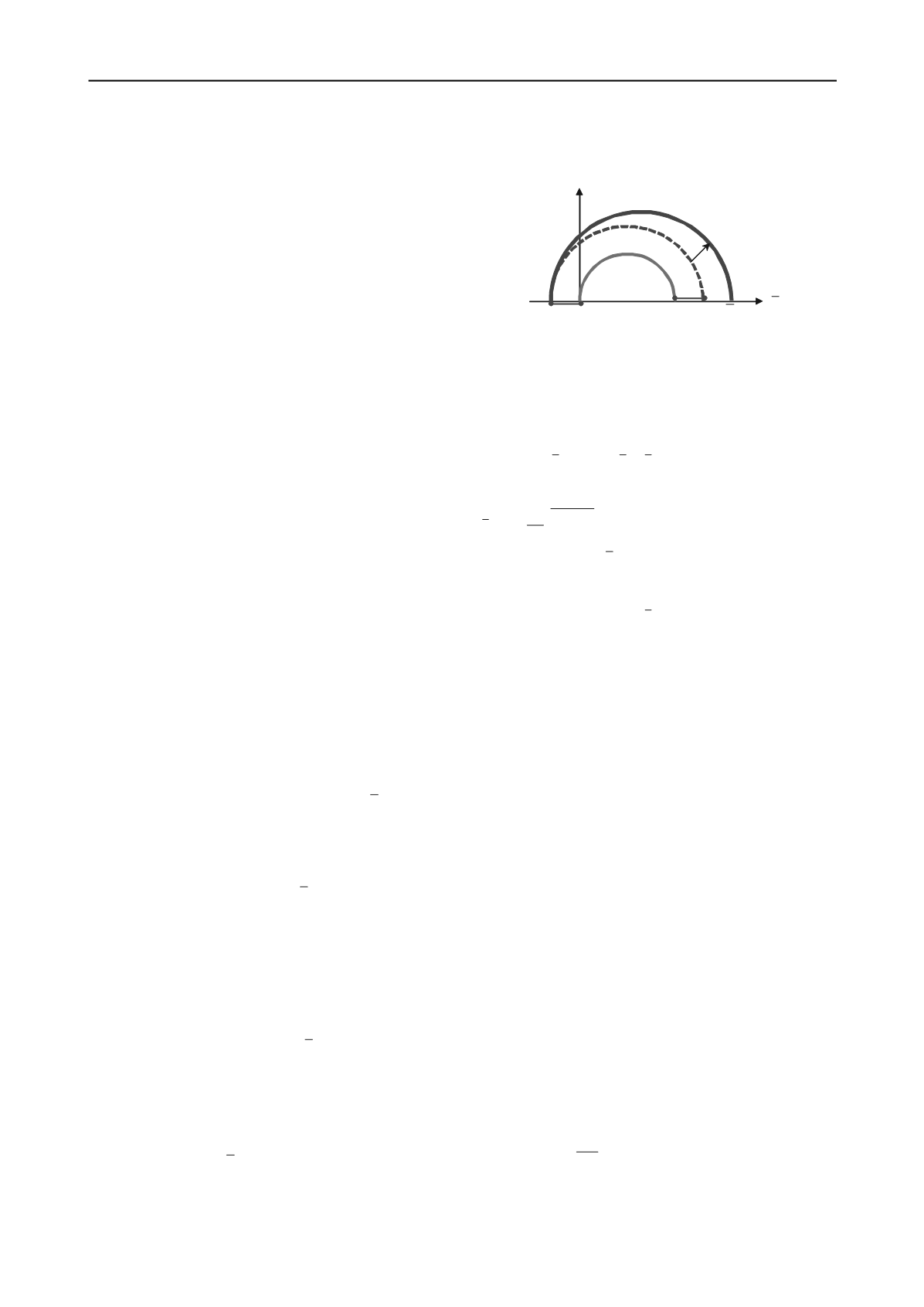
ice (Figure 2).
p
q
T>0
C
“Unfrozen”
T<0
C
“
Frozen
”
0
p
c
p
sS k
i
s
Plastic
hardening
Figure 2. Yield surface of porous material in frozen and unfrozen regions
The increase in the bonding strength is assumed to be equal in
the direction of compression and tension, and be proportional to
strength ratio
(Nishimura, et al., 2009) and pore volume
fraction of ice
.
s
k
i
S
)
1(
l
S
(10)
where pre-consolidation pressure can be expressed as
sS k
p
p
p p
i
s
s
s
r
r
c
)( )(
)0( )0(
0
(Alonso, et al. 1990). Above
freezing temperature,
c
p
is the same as
, however it evolves
nonlinearly below freezing temperature from suction and ice
pressure development.
is reference stress, and
M
is the
slope of critical state line in
0
p
i
P
r
p
qp
space. Compression index at
various suction is
r
r
s
exp 1
)(
s
)0(
, and swelling
index
)(
s
is assumed to have the same function of suction as
compression index for numerical stability.
Mechanical plastic potential function determining
incremental direction of plastic deformation follows associated
flow rule
f g
, and strain-rate-dependent characteristic of
frozen soil is not considered in this model.
3.4. Strain components
Total strain increment can be divided into mechanical strain
from stress variable, thermal strain, and phase change between
liquid water and solid ice in the pore. In addition, mechanical
strain increment has elastic and plastic mechanical strain parts.
ph
T
mp
me
ph
T
m
d
d
d
d
d
d
d d
~
~
~
~
~
~
~ ~
(11)
where
elastic
mechanical
strain
increment
is
(Sheng
et
al.,
2008),
and
is (elastic stiffness tensor).
~
1
~
~
:
d D
d
e
me
~ ~
~
11)3/ 2 (
G K D
e
~
2
IG
K
and
are elastic buck and shear modulus, and
~
1
,
.
G
kl
ij
~
1
2/)
(
~
jk il
jl
ik
I
Temperature-dependent volumetric change in elastic region is
determined from thermal elastic contractile coefficient ( ),
T
dT
dT
T
d
d
T
e
v
Te
v
T
v
3
. And volumetric strain due to
phase change is the following from conservation of water mass.
where and
are mass density of water in liquid and
solid phase, and strain due to phase change can be expressed as
w
l
w
i
0
2
2
p psS k pM q f
c
i
s


