1668
Proceedings of the 18
th
International Conference on Soil Mechanics and Geotechnical Engineering, Paris 2013
k
est le tenseur de perméabilité de Darcy, g est l’accélération de
la pesanteur,
est la contrainte partielle dans la phase solide
et
est la pression dans le fluide. Pour un milieu isotherme et
isotrope les relations contraintes-déformations s’écrivent :
s
σ
w
p
w w s
sw
w
w sw s
s
ε I
ε I
σ
ε I
εE σ
:
:
:
:
s
(3)
où
est le tenseur d’élasticité,
s
est le tenseur de
déformation de la phase solide,
w
ε
est le tenseur de déformation
de la phase liquide,
δ
est le symbole de Kronecker,
est la
contrainte partielle dans la phase liquide et
s
E
ε
w
σ
sw w s
,
,
and
s
sont les paramètres élastiques du milieu poreux.
3 MODELE DE COMPORTEMENT
Comme pour les milieux solides, le taux de déformation dans la
phase solide
est divisé en une partie élastique
et une
partie plastique . Les équations de comportement s’écrivent :
ε
p
ε
e
ε
ws
p e
,
,
ε ε ε
(4)
p
s
w
s
p
w
p
s
n
n
t
and
with
εtr
εr
0
ε
P
(5)
)
(:
p
s
s
ε εE σ
(6)
σ
est le tenseur taux de contraintes effectives de Cauchy et
P
est le potentiel plastique.
3.1 Fonction de charge
Le modèle multi-surfaces de Prévost développé en 1988 a été
adapté aux sollicitations tridimensionnelles telles que celles
générées par les séismes. Les surfaces de charge d’Eekelen
(1980) circonscrites aux pyramides de Mohr-Coulomb ont été
utilisées (Zerfa, 2003). L’équation de ces surfaces est donnée ci-
après :
0
3
2
, ,
pMR
p
M f
α s
ασ
(7)
tan
3
1
c
tr
p
σ
(8)
s
est le tenseur déviatorique,
est le tenseur qui définit l’axe
des surfaces de charge, M définit la taille des surfaces de
charge, c est la cohésion et
est l’angle de frottement interne
mobilisé.
Plusieurs relations ont été proposées pour décrire la forme
des surfaces de charge dans le plan déviatorique. Néanmoins, la
forme proposée par Eekelen (1980) semble la plus appropriée
car elle reste convexe pour des angles de frottement interne
élevés. Elle est décrite par l’expression suivante de
R(
) :
n
R
3 sin 1
(9)
,
et n sont des paramètres de sol à déterminer à partir d’essais
triaxiaux en compression et en extension.
est l’angle de Lode.
Figure 1. Surfaces de charge d’Eekelen et de Mohr-Coulomb
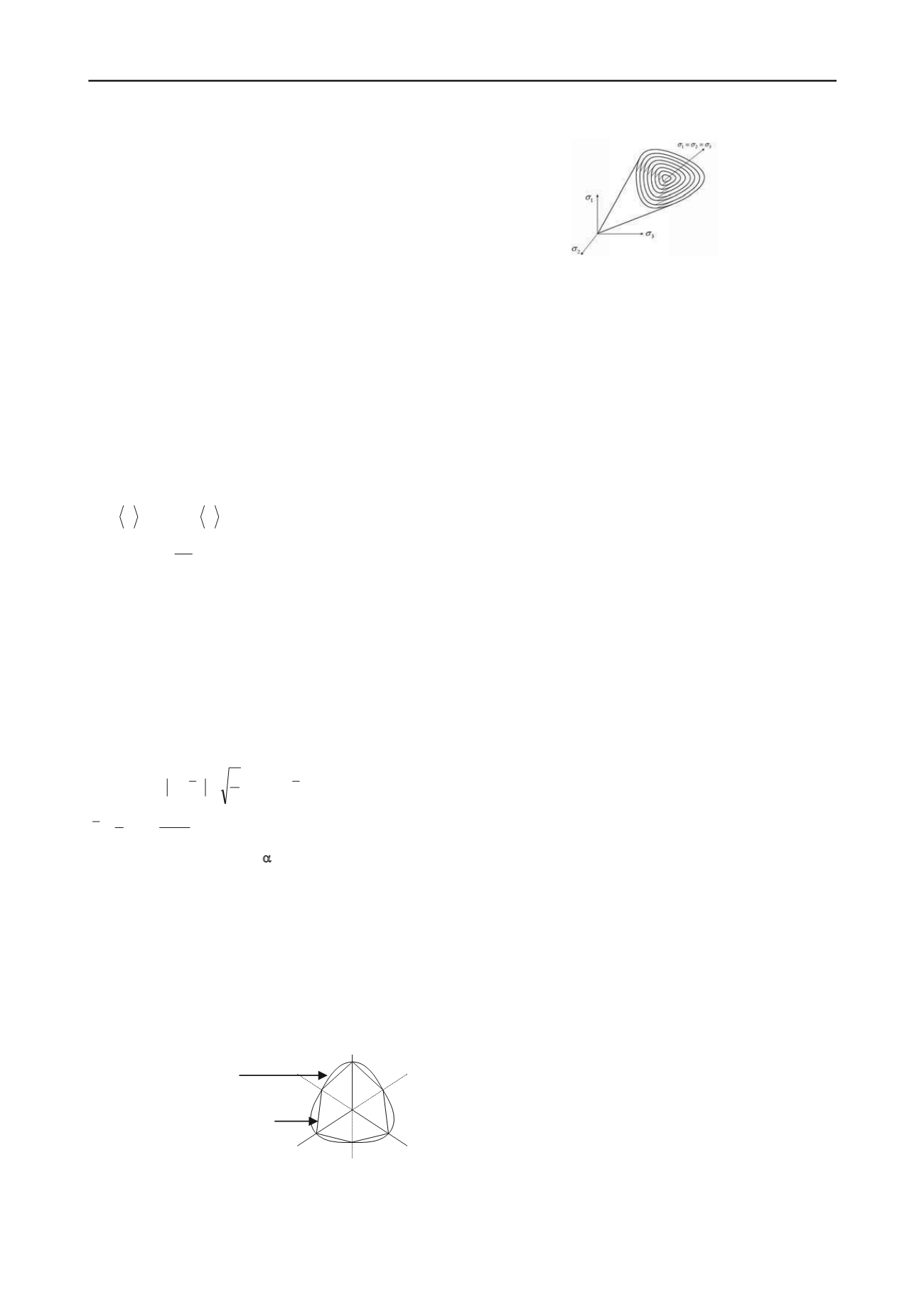
Dans l’espace des contraintes effectives, les surfaces de charges
ayant le même axe, sont imbriquées les unes dans les autres tel
que le montre la figure 2.
Figure 2. Surfaces de charge imbriquées à axe unique
3.2 Loi d’écoulement
Le potentiel plastique est décomposé en une partie déviatorique
associée et une partie sphérique non associée.
3.3 Règle d’écrouissage
L’écrouissage est purement cinématique. Les surfaces de charge
activées sont translatées à partir de leur position initiale par leur
point de contact de manière à éviter leur chevauchement.
3.4 Algorithme d’intégration de la loi de comportement
Afin d’intégrer les équations constitutives définies par les
expressions 4 à 6, l’algorithme du plan sécant (Prévost, 1988,
Simo and Hughes, 1987) a été utilisé. Il a l’avantage d’être
adapté à des formes de surfaces quelconques mais convexes.
Néanmoins, le problème majeur de cet algorithme réside en
son incapacité à converger lorsque le point de contrainte se
retrouve à l’arrière du sommet des surfaces de charge.
L’apparition de la liquéfaction correspond à ce cas. De ce fait,
dès que la liquéfaction apparait en un point du modèle, les
calculs ne peuvent plus être poursuivis.
4 FRONTIÈRES ABSORBANTES
4.1 Formulation mathématique
En dynamique, l’étude de l’interaction sol-structure joue
un rôle important. La taille de la partie de la fondation à prendre
en compte et les conditions aux limites à considérer influencent
énormément les réponses des structures. Ainsi, afin de pouvoir
remplacer le système semi-infini par un milieu fini équivalent,
limité par ce qu'on appelle une frontière absorbante, le
comportement à l’infini doit être précisé.
Dans un système infini, les ondes se propagent de la
source vers l’infini alors que dans système fini elles sont
réfléchies vers la source lorsqu’elles atteignent les limites du
modèle. Les conditions aux limites doivent donc stipuler
qu’aucune énergie ne doit être réfléchie par la limite artificielle
vers la structure. C’est ce qu’on appelle la condition de
radiation.
Différents méthodes ont été proposées afin de
solutionner le problème. La première suggère de borner le
domaine par une limite artificielle qui coïncide avec la limite
artificielle. Les conditions aux limites imposées à cette frontière
consistent à lui assigner la condition de radiation. Dans le cadre
de cette méthodologie, la première idée fut développée par
Lysmer et Kuhlmeyer [19,21]. Ils proposent de compenser
l’énergie réfléchie par des amortisseurs répartis sur toute la
frontière artificielle. Cette méthode présente l’avantage de
conduire à des équations qui ne dépendent pas des fréquences
du système, qui sont faciles à intégrer dans les équations
d’équilibre et qui conduisent à des résultats acceptables. Cette
technique qui s’est avérée assez pratique a été adaptée aux
milieux poreux (Zerfa, 2004) en considérant une formulation
u
s
-
u
w
des équations d’équilibre.
'
'
'
Surface de charge d’Eekelen
Surface de charge de Mohr-Coulomb
Les contraintes visqueuses qui doivent absorber aux frontières
du modèle, l’énergie des ondes réfléchies s’écrivent sous la
forme suivante :


