1469
Technical Committee 203 /
Comité technique 203
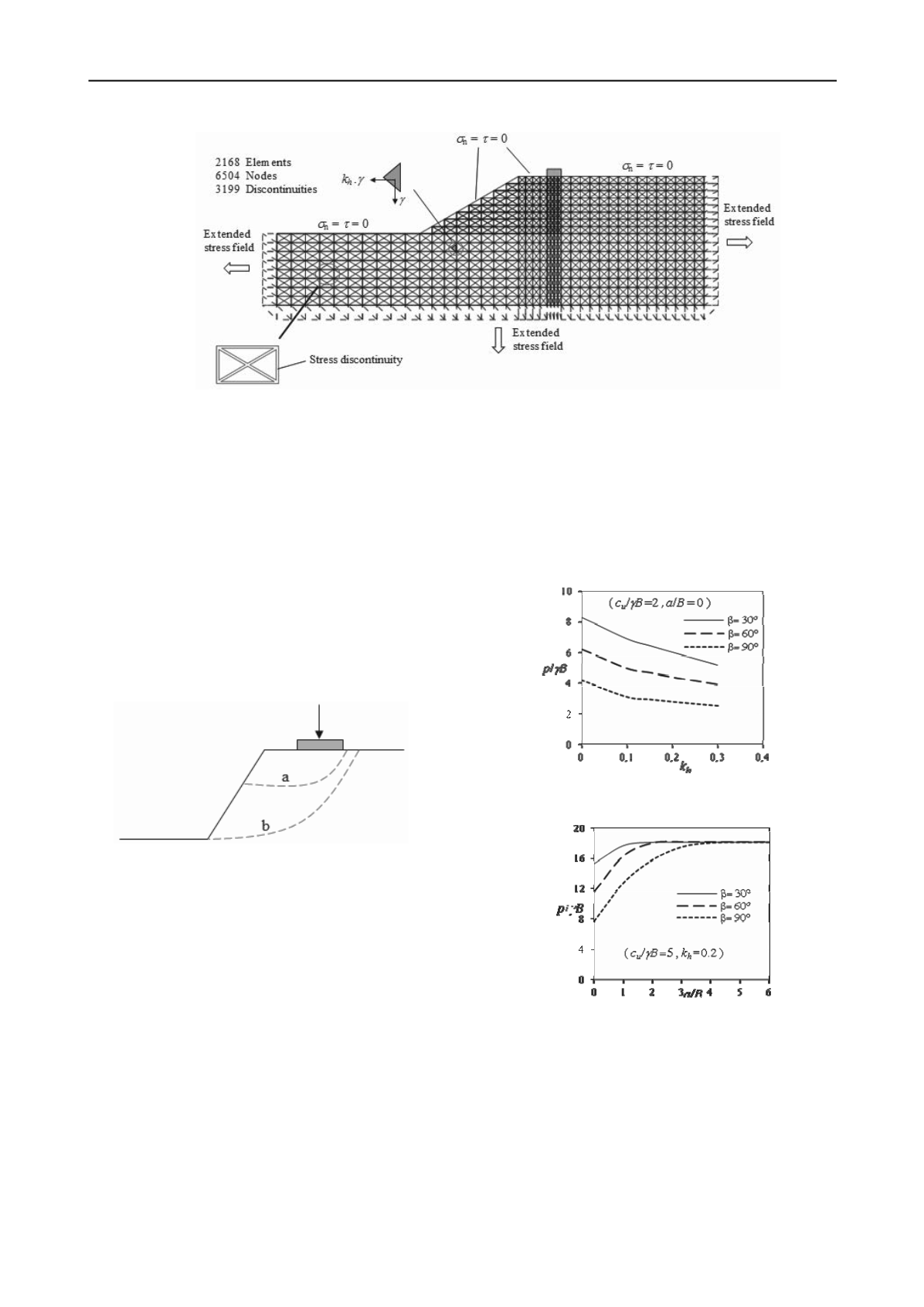
Figure 5. Typical finite element mesh used in lower bound analysis (
=30
,
a
/
B
=2)
4 DETAILS OF ANALYSES
A typical finite element model used in lower bound analysis for
a problem with
=30
and
a
/
B
=2 is illustrated in Figure 5 which
consists of 2168 elements, 6504 nodes and 3199 stress
discontinuities. It should be mentioned that in all of the finite
element models of current study, statically admissible stress
discontinuities are considered at all shared edges of adjacent
elements.
For a footing-on-slope system, the ultimate bearing capacity
of the footing may be governed by either the foundation bearing
capacity or the overall stability of the slope. The combination of
these two factors makes the problem difficult to solve (Shiau et
al. 2011).Typical mechanisms of these two failure modes are
illustrated in Figure 6.In current paper, the bearing capacity
mode is investigated in analyses.
Figure 6. Typical failure modes for footing-on-slope system: bearing
capacity mode (a) and overall slope failure (b).
A wide range of parameters has been examined in analyses.
Three slope angles
=30
,60
,90
,horizontal acceleration
coefficients of
k
h
=0, 0.1, 0.15, 0.2, 0.25,0.3 and various ratios
of
a
/
B
and
c
u
/
B
were considered. According to results, the
value of
H
/
B
=4insures that the bearing capacity mode (mode a)
will occur for all values of
k
h
mentioned above. So,
H
/
B
=4was
considered in all models.
5 RESULTS AND DISCUSSION
The effects of various parameters on seismic bearing capacity of
strip footings near cohesive slopes were examined. Figure 7
shows the variation of dimensionless bearing capacity (
p
/
B
)
with the seismic coefficient (
k
h
) for a problem with
c
u
/
B
=2 and
a/B
=0.
As can be observed, the bearing capacity decreases as the
horizontal acceleration increases. The bearing capacity reduces
more steeply from
k
h
=
0 to 0.1with respect to
k
h
=0.1 to 0.3. It is
also seen that the decline of bearing capacity for the second part
of diagrams (
k
h
≥
0.1) intensifies as the slope angle reduces. For
example, the dimensionless bearing capacity of a slope with
=30
changes from 6.88 to 5.16 (roughly 25% reduction) as
k
h
increases from 0.1 to 0.3. This reduction is about 21.5 % for
=60
and 19% for
=90
The influence of relative distance of the footing (
a
/
B
) on
seismic bearing capacity of a footing-on-slope problem is
illustrated in Figure 8 for
c
u
/
B
=5,
k
h
= 0.2 and various slope
angles.
Figure 7. Variation of dimensionless seismic bearing capacity with
seismic coefficient
k
h
Figure 8. Variation of seismic bearing capacity with
a
/
B
The bearing capacity increases when footing distance from
the slope crest increases and from a definite value of
a
/
B
the
bearing capacity remains constant. This means that the effect of
slope diminishes as the foundation goes far from the slope crest
and the bearing capacity approaches the bearing capacity of a
footing on level ground. It can also be observed that the footing
which rests on a slope with lower angle reaches to this constant
value more rapidly. The other parameter which has a great
effect on seismic stability of strip footings near slopes is the
dimensionless strength of
c
u
/
B.
Results show that the variation
of
p
/
B
is linear for a definite range of this parameter (Figure 9).


