1468
Proceedings of the 18
th
International Conference on Soil Mechanics and Geotechnical Engineering, Paris 2013
in which
p
is the average vertical limit pressure under the
footing base. The effects of these parameters on bearing
capacity of so-called system will be discussed in the following
sections.
3
3
3
1
1
1
;
;
l
l
xy l
xy
l
l
y l
y
l
l
x l
x
N
N
N
x
y
xy
y
; .
k
y
x
h
xy
x
2
2
2
0 ) 2( ) 2( )
(
u
xy
y
x
c
F
σ
T
c
2
2
1
1
b A
b A
σ
σ
3 FINITE ELEMENT FORM OF LOWERBOUND
LIMITANALYSIS
The lower bound limit theory (Drucker et al. 1952) may be
stated as: “If all changes in geometry occurring during collapse
are neglected, a load obtained from a statically admissible stress
field is less than or equal to the exact collapse load.”
A statically admissible stress field is one which satisfies
equilibrium and boundary conditions and nowhere violates the
yield criterion.
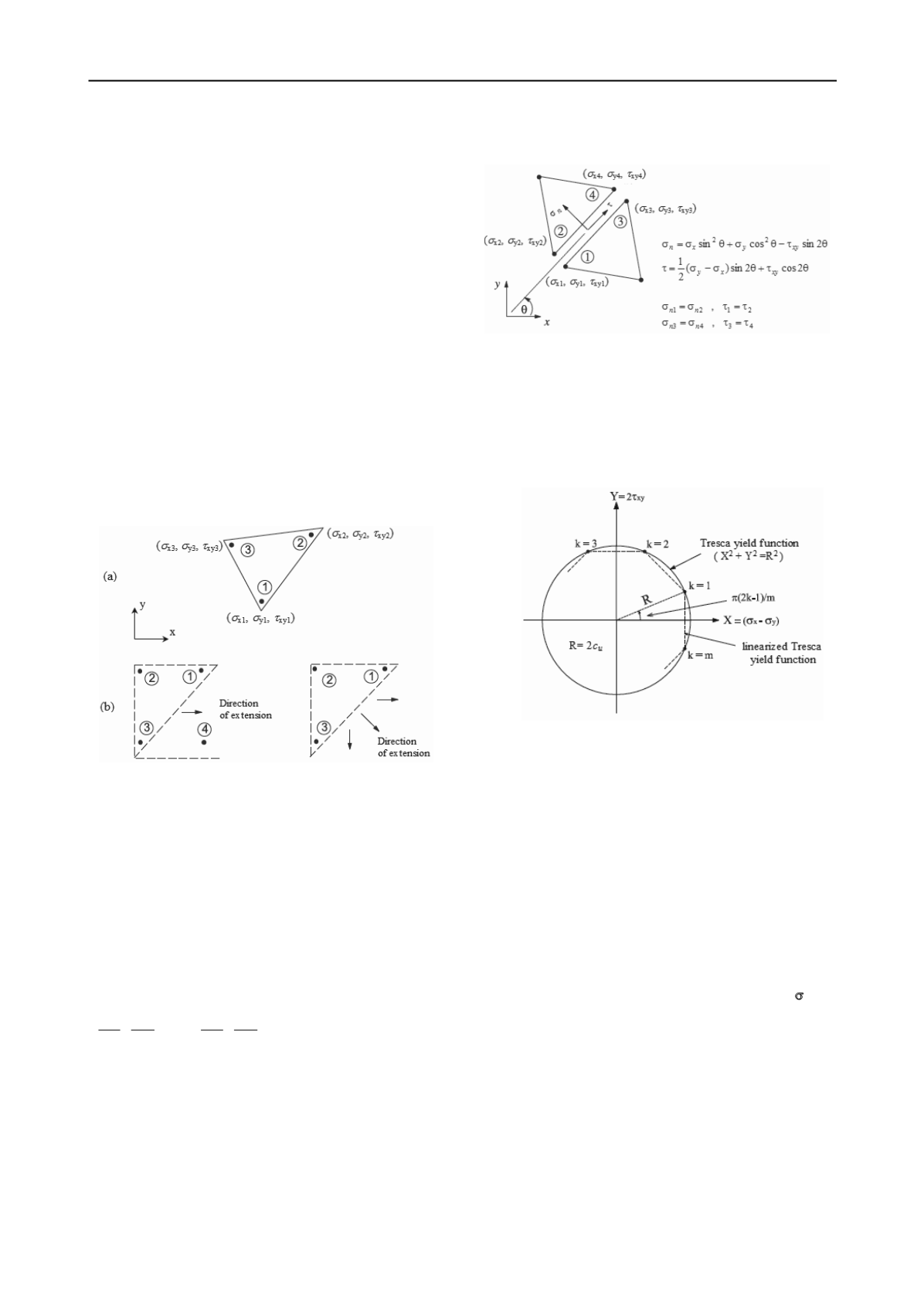
The formulation used in this paper follows that of Sloan (1988)
in which the linear finite element method is applied and the
domain of problem is discretized by 3-noded triangular
elements. Unknowns of the problem are nodal stresses (
x
,
y
,
xy
). Figure 2 shows the typical elements used in lower bound
analysis. Extension elements are used to extend the statically
admissible stress field into a semi-infinite domain and thus lead
to a rigorous lower bound solution.
Figure 2.Typical linear triangular element (a) and extension elements
(b) used in lower bound analysis (Shiauet al. 2003)
Using linear finite element method, the stresses vary linearly
throughout each element according to:
(2)
where
x
,
y
and
xy
are nodal stress components and
N
l
are linear shape functions.
l
l
l
For present problem where the pseudo-static force acts
outward the slope and the vertical acceleration of the earthquake
is ignored, equilibrium equations for a right-handed
x
-
y
coordinate system can be stated as:
(3)
where
k
h
=a
h
/g
is the horizontal acceleration coefficient of
earthquake. Combination of equations (2) and (3) leads to a
matrix form of element equilibrium equations.
The main difference between a lower bound mesh and a
classic finite element one is that some nodes may have the same
co-ordinate. Thus, the statically admissible stress discontinuities
can occur at shared edges of adjacent elements (Figure3).
Figure 3. Statically admissible stress discontinuity
The undrained behavior of clays (
u
=
0) can be modeled by
Tresca yield criterion and can be expressed as following
nonlinear equation in plain strain condition:
(4)
in which tensile stresses are taken as positive (sloan 1988).
Figure 4. Linearized Tresca yield function
In order to use linear programming technique, the linearized
Tresca yield function should be utilized in formulation of lower
bound theory. For this purpose, the nonlinear yield criterion is
approximated by an interior polygon in lower bound limit
analysis (Figure 4).
By assembling all equalities and inequalities, a discrete
formulation of the lower bound theory leads to the following
constrained optimization problem:
maximize
:
subject to
:
(5)
where cis a vector of objective function coefficients,
is the
vector of problem unknowns, A
1
is an overall matrix of equality
constraint coefficients which derives from elements
equilibrium, discontinuities equilibrium and boundary
conditions, b
2
is a right-hand vector of equality coefficients, A
2
is an overall matrix of inequality constraint coefficients which
derives from yield criterion and b
2
is the corresponding right-
hand vector. Using linear finite elements and linearized yield
function, the lower estimation of true collapse load can be
obtained through linear programming techniques. In current
study, the “active-set” algorithm is used for optimization of
lower bound limit load.


