917
Technical Committee 104 /
Comité technique 104
5.1
Consolidation
The first step in the centrifuge model test is to reconsolidate the
clay model in-flight at an acceleration of 50 g, due to the
increase in self-weight. Dissipation of the excess pore water
pressures took approximately 13 h (Fig. 4).
5.2
Stone column installation
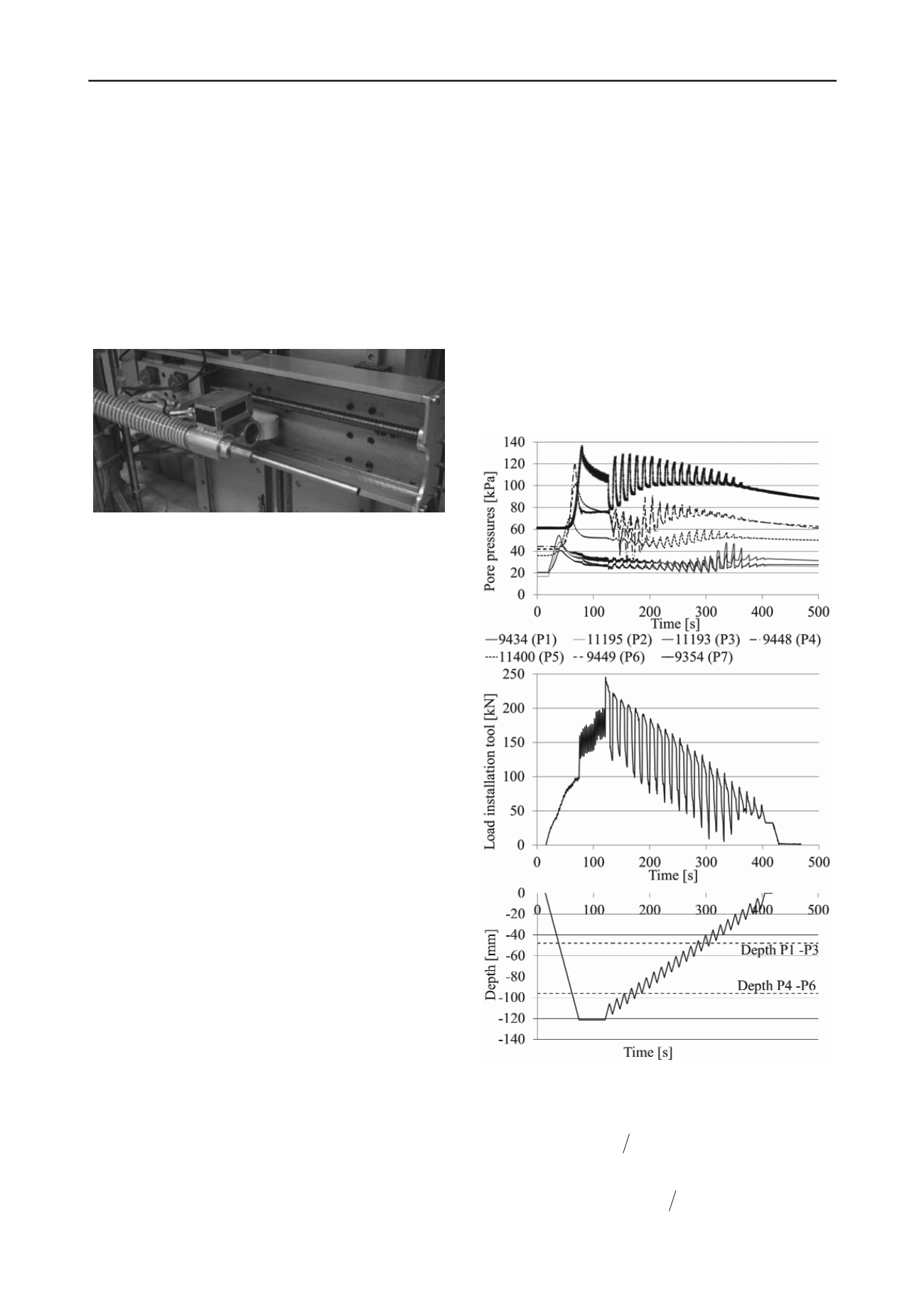
The stone column installation tool developed by Weber (Fig. 5;
Weber, 2008) has been used to construct the stone column. It
consists of a steel tube with an outer diameter of 10 mm and an
inner diameter of 8 mm. A drawing pin was used to prevent the
tube from blocking during first penetration.
Fig. 5: Stone column installation tool (Weber, 2008).
The column tool was inserted up to a depth of 120 mm in the
centre of the clay model and the column was built with a 15/10
compaction regime (i.e. once the desired installation depth was
reached, the tool was extracted by 15 mm before being inserted
again 10 mm, compacting the sand in the column). This
compaction process increases the stone column diameter to 12
mm (see Fig. 1), at least in the softest clay layer near the
surface. The insertion was displacement-controlled (2 mm/s)
and the driving force as well as the pore water pressures were
recorded during this phase (Fig. 6). The development of pore
water pressure over time is given in the top part of Fig. 6. The
middle part of Fig. 6 shows the scaled driving force required to
penetrate the installation tool and the bottom part shows the
position of the tip of the installation tool under the surface. It
can be seen that the strongest reaction of the PPTs is observed
when the tip of the column tool reaches the depth of the sensors
(marked by horizontal dashed lines in the Fig. 6c). This is
observed both for the penetration phase and the compaction
phase, respectively.
90% of the excess pore water pressures are dissipated after
about 2300 s, which, when scaled by 50
2
, corresponds to a
prototype time of about 67 days. This is significantly shorter
than the time needed for dissipation of excess pore pressures at
the beginning of the test (see Fig. 4). Indeed, for a drainage path
of 4 m (half of the prototype height of the model) and a one
dimensional stiffness modulus M
E
= 1780 kPa, a coefficient of
consolidation
7 2
2.67 10
/
v
c
m
2
/
589
d c
s
s
is obtained, leading to a
consolidation time at 90% excess pore water pressure
dissipation of
90
90
v
v
t
T
. This reduces the time
by a factor of 8.8, which is consistent with a combined drainage
condition, i.e., vertical plus radially outwards (to the
surrounding Perth sand) and inwards (towards the stone
column) resulting from the insertion of the granular column.
day
6 FOOTING LOADING
As the third step in the test, the newly built stone column
was loaded with a 56 mm-diameter stiff aluminium footing,
after the excess pore water pressures caused by the installation
of the column had dissipated. The loading was displacement-
controlled (v = 0.02 mm/s) and a maximum settlement of
17 mm at model scale was attained before the footing was
removed and the loading-induced excess pore water pressures
were left to dissipate. The first jump in excess pore water
pressures (Fig. 7 top) between 0 and 1000 s is due to a technical
problem, which triggered an unexpected loading of the stone
column. The actual loading can thus be studied after 1000 s.
The sensors P1 (top layer close to the column) and the
sensors P4, P5 and P6 in a depth of 96 mm below ground
surface react in parallel to the loading, albeit with different
magnitudes of pore pressure change, while P2 and P3 exhibit a
less sharp response. This confirms that the column takes a larger
part of the load than the soft clay and the pressure distribution
with depth is not building up as it would in a homogeneous
medium. Secondly, an explanation was sought for the increase
(P1 to P6) or drop (P7) in pore water pressures that can be seen
at about 1500 s, which might have coincided with failure of the
column. A bulge could be identified in the upper third of the
column as the model was being dismantled. The cause might be
attributed to the development of this ‘local compression failure
zone’ in the sand column.
(a)
P7
P4-P6
P5
P1-P2-P3
(b)
(c)
Fig. 6: (a) Pore water pressures, (b) driving force (c) depth of the tip of
the installation tool during the sand column installation.
The total load applied on the footing can be formulated as
(Adam, 2011):
v
sc sc
clay clay
sc
clay
A
A A A
(1)
with the
corresponding load on the stone column as (Adam,
2011):
'
'
1 sin
2
1 sin
sc
sc
clay
clay
sc
c
(2)


