1358
Proceedings of the 18
th
International Conference on Soil Mechanics and Geotechnical Engineering, Paris 2013
3 EVALUATION OF THE SWELLING DEFORMATION
The great volumetric expansion and contraction potential of
these soils can be explained empirically through a direct
correlation to plasticity index (from Texas Department of
Transportation method TEX-124-E, “Vertical Rise Potential”)
or from a theoretical approach (Little 2012). In the latter
approach matrix suction is related to volume change. The
change from the matric suction that exists under a current or
existing moisture regime to a state of drying (where the matric
suction increases) or to a state of wetting (where the matric
suction decreases) is the trigger of volume change. This
volumetric change was determined by Mitchell (1980) as a
function of depth, soil type, and climatic conditions using the
following relationship:
0.5
0
exp
z
e
n
U U U
z
[1]
Where U
e
is equilibrium suction, U
0
is the amplitude of
suction variation, n is the number of cycles of wetting and
drying within a year, α is diffusion coefficient, and z is depth.
The difference between a current or initial (U
i
) and final
suction (U
f
) as determined from equation [1] can be used to
estimate the range of volume changes of the natural soils below
the pavement structure. The volumetric strain is calculated
using the following relationship (after Hong et al, 2006 and
Bulut, 2001):
10
10
10
10
log
log
log
log
f
f
h
swelling
i
i
f
h
shrinkage
i
U
V
V
U
U
V
V
U
f
i
[2]
Where
V
V
is volumetric strain, γ
h
is suction
compressibility index, and σ
i
and σ
f
are initial and final
overburden stress, respectively. From this relationship it is
important to note that, first, volume change, whether shrinkage
or swelling is driven by a difference between initial and final
matric suction, U. Second, the impact of the driving force for
volume change, ∆U, on volume change is determined by the
suction compressibility factor, which operates in this
constitutive relationship like a modulus in stress-strain
constitutive relationships.
The result of the physico-chemical changes achieved through
lime treatment of the clay soils had the practical effect of
making the most highly susceptible soils to volume change
within the active zone practically non-susceptible to volume
change. As shown by equation 1, this active zone depth is
influenced by climatic variables such as n and soil variables
such as diffusivity, α. As one can visualize from equation 1, the
upper portion of the active zone provides the greatest driving
force, ∆U. Since it is the active, natural clay in this upper zone
which is contributing more to the pavement movement, an
envident remedial measure to replace this layer in large portion
by an inert soil or the same natural clay treated with lime. In
doing so, the swell and shrink volume change potential is
greatly mitigated.
Suction values at depth for the application of equation 1 have
normally a minimum suction value of U = 2.0pF and a
maximum suction value of U = 4.5pF as measured in semi-arid
zones. The suction values at the surface do not have limits and
depend solely in the climatic region.
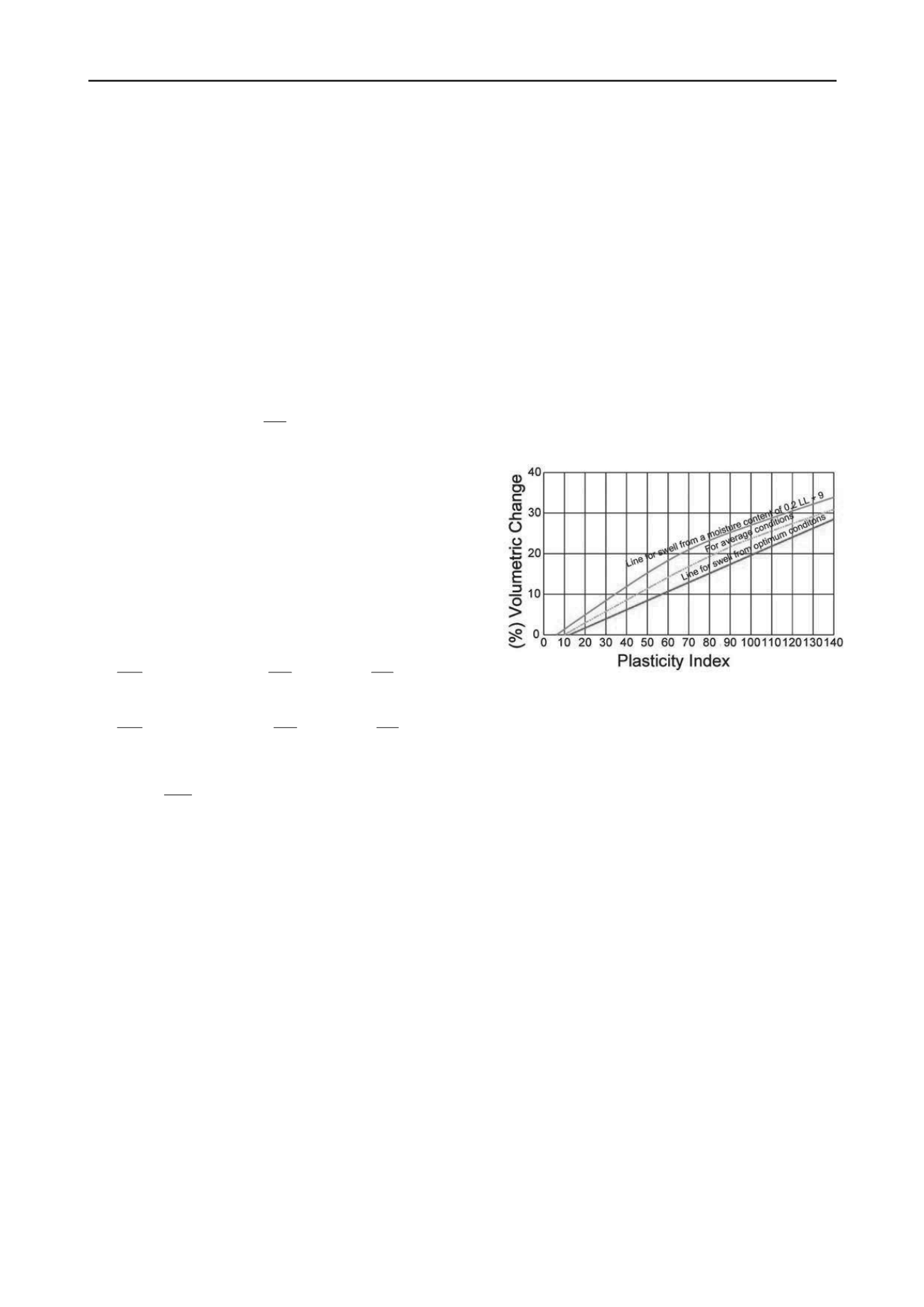
4 POTENTIAL VERTICAL RISE (PVR)
Texas method (TEX-124-E), is widely used in Texas to
determine the required depth of replacement of expansive soils
with inert soils, based on the expansion characteristics of the
soils.
This standard determines the Potential Vertical Rise
(PVR) in soil strata, which is described as the “
latent or
potential ability of a soil material to swell, at a given density,
moisture, and loading condition, when exposed to capillary or
surface water, and thereby increase the elevation of its upper
surface, along with anything resting on it
”. Figure 3 shows the
correlation between the PI of the soil and the volumetric change
due to swelling.
Figure 3. Graph Plasticity Index vs. Percent Volumetric Change.
From Tex-124-E
However, this method has a series of shortcomings:
1. Soil at all depths has access to water in capillary
moisture conditions.
2. Vertical swelling strain is assumed as one-third of the
volume change at all depths.
3. Remolded and compacted soils adequately represent
soils in the field.
4. PVR of 0.5 inch (or 1 inch) produces unsatisfactory
riding quality.
5. Volume change can be predicted by use if the plasticity
index alone.
5 LABORATORY EVALUATION OF SWELLING
Twelve samples from five boreholes were collected from a
project in south Austin. The samples were selected to provide
three replicate samples within a lower (<40%), intermediate (40
to 60%) and high (>60%) range of plasticity indices.
5.1 Comparison with the PVR analysis
The following laboratory tests were completed:
Material passing 75 microns.
Oedometer tests and free swell.
Atterberg limits.
Suction potential by pressure plate method.


