1299
Technical Committee 202 /
Comité technique 202
4.6
Step 6 – Determination probability of exceedance
For every simulation a set of spring values was generated.
With the soil-structure interaction model the bending moment
and vertical force equilibrium the rotation and (average)
settlement was calculated for every set of springs. The
probability of exceedance for a certain rotation can be estimated
by:
n n
P
f
r
/
)
θ(
(19)
In which:
P(θ>
θ
r
) = exceedance probability of rotation
θ
r
[-]
n
f
=
number of simulations for which the calculated
rotation is larger than the reference rotation [-]
n
=
total number of simulations [-]
The accuracy of this estimate strongly depends on the
number of simulations in relation to the probability of
exceedance; for smaller probabilities, a higher number of
simulations is necessary to reach the same reliability of the
estimation. The relative error
is given by (CUR190, 1997):
))
θ( /)
θ(
/ (
r
r
f
P
Pn n
(20)
For a certain value of the relative error E with an accuracy of
95% can be estimated by:
) /)1 / (4(
n
nn
E
f
(21)
For this study a relative error E of maximum 20% is
assumed to be acceptable. In order to be able to determine
probabilities of exceedance of 1·10
-4
sufficiently accurate,
therefore at least 1·10
6
simulations are necessary.
5
RESULTS AND APPLICATION
5.1
Results
Figure 4 shows the results of realisations for the residual
rotations of pier 40. In this figure the combined realisations of
rotation around the long axis (
θ
x
) and the rotations around the
short axis (
θ
y
) are shown.
Figure 4. Results Monte Carlo analysis pier 40, residual rotations
Figure 4 shows that the distribution of realisation is located
around the origin what means that the expected rotation is more
or less equal to zero. This is in line with the deterministic
settlement calculations. It is also shown that rotation around the
long axis has a higher probability than rotation around the short
axis. The shortest side (width) of the foundation block is more
sensitive for rotation.
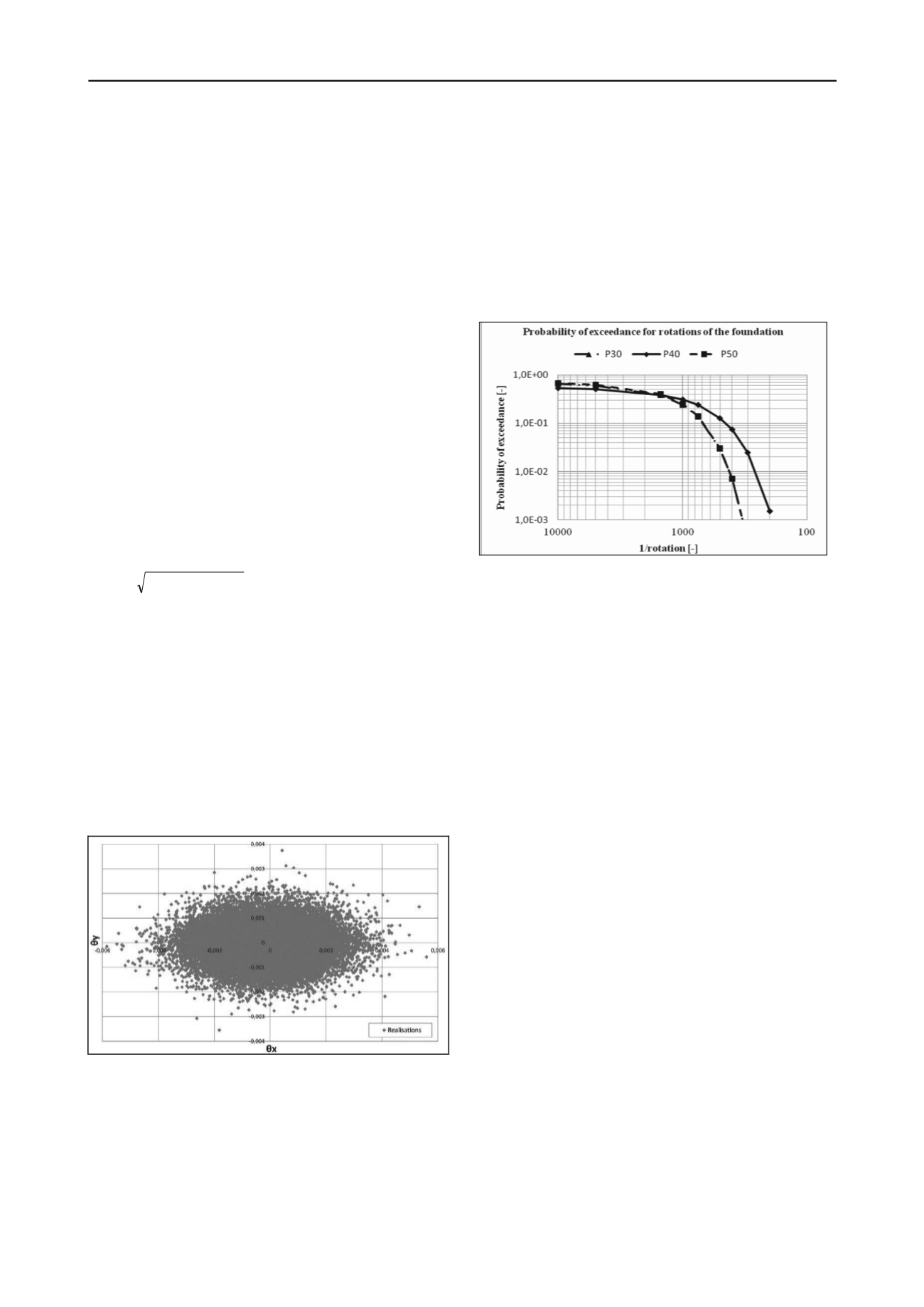
The calculated probabilities of exceedance for different
rotations are presented in Figure 5 for the rotation around the
long axis (
θ
x
). The results for pier 30 and 50 are almost equal
because the calculated deformations with the FEM model are
also almost equal for these piers. From Figure 5 related to the
average settlement of the piers it can be concluded that larger
average settlements (pier 40) result in a higher probability of
larger rotations, which is reasonable.
Important for the bridge deck is the combined rotation of two
piers. Based on the results of the individual piers also the
probability of a combined rotation of two piers could be
determined. For the combined rotation it is assumed that the
deformation behaviour of the piers is uncorrelated.
Figure 5. Results probabilistic deformation analysis (
θ
x
)
. Note that the
results for P30 and P50 are almost identical
5.2
Application of results
The results of the model are used for the design of the
different components of the bridge which are influenced by the
settlement and rotation of the pier.
Based on the calculated probability of exceedance of a
certain rotation, safe boundary conditions for the other design
disciplines could be determined. Relevant components are the
towers with the guiding system, the deck, the expansion joints
for the deck and the supports of the deck. A design value of the
deformation is derived for these components based on the
acceptable probability of exceedance.
During construction the deformations will be monitored and
control measures can be applied if necessary.
6
CONCLUSION
For the design of the new Botlek Lifting Bridge soil
deformations can potentially have a major affect on one of the
most critical design requirements, which is a limited rotation of
the large foundation footing.
Alongside a well designed site investigation campaign,
laboratory tests and the application of appropriate constitutive
models, a quantification of the probability of exceedance of soil
deformations was desired. Application of a simplified stochastic
subsoil model enabled a quantitative risk analysis in order to
deal with the uncertainties described in this paper.
Based on the calculated probability of exceedance of a
certain rotation, safe boundary conditions for the other design
disciplines could be determined.


