1052
Proceedings of the 18
th
International Conference on Soil Mechanics and Geotechnical Engineering, Paris 2013
translational angular velocities of the particle.
F
c
ij
= the contact
force acting on Particle
i
by Particle
j
or the wall(s);
M
ij
= the
torque acting on Particle
i
by Particle
j
or the wall(s);
n
c
i
= the
number of total contacts for Particle
i
;
F
f
i
= the particle–fluid
interaction force acting on particle
i
;
F
g
i
= the gravitational
force.
m
i
= the mass of Particle
i
;
I
i
= the moment of inertia of
particle
i
.
U
f
= the average velocity of the fluid cell.
n
denoting
the porosity.
f
= the averaged fluid density.
p
= the fluid
pressure in the cell;
μ
= the averaged viscosity;
f
p
= the
interaction force averaged by the cell volume the particles
inside the cell exert on the fluid.
g
= the body force vector.
The proposed numerical CFD-DEM approach solves
eq
DEM is the
pro
uation system in (1) as follows. The fluid phase is discretized
with a typical cell size several times of the average particle
diameter. At each time step, the DEM package provides such
information as the position and velocity of each individual
particle. The positions of all particles are then matched with the
fluid cells to calculate relevant information of each cell such as
the porosity. By following the coarse-grid approximation
method proposed by Tsuji et al. (1993) (see also, Zhu
et al.
,
2007), the locally averaged Navier-Stockes equation is solved
by the CFD program for the averaged velocity and pressure for
each cell (the flow along individual pore pathways in the
mixture will not be modeled by this method). These obtained
averaged values for the velocity and pressure of a cell are then
used to determine the drag force and buoyancy force acting on
the particles in that cell. Iterative schemes may have to be
invoked to ensure the convergence of relevant quantities such as
the fluid velocity and pressure. When a converged solution is
obtained, the information of fluid-particle interaction forces will
be passed to the DEM for the next step calculation.
Key to the coupling between the CFD and the
per consideration of particle-fluid interaction forces.
Targeting at geomechanics applications, three interaction forces
are considered in this study: the drag force, the buoyancy force
and the virtual mass force. The drag force adopts the expression
by Di Felice (1994)
2
1
8
p
f
p
d f
p
C d
n
1
d
f
F
U U U U
(2)
Where
d
p
= the diameter of the considered particle;
C
d
= the
particle-fluid drag coefficient which depends on the Reynolds
number of the particle Re
p
where
Re
f
p
p
f
n d
p
U U
;
ge
2
10
g Re
p
0.5 1.5 lo
3.7 0.65
e
. While for the buoyancy force, we
employ the following avera density based expression
3
1
b
f
d
F
6
p
g
(3)
The virtual mass force i
added to a particle accelerating or decelerating in a fluid which
ma
s considered to reflect the inertia
y deflect certain volume of the sounding fluid to move
through. In this study the following expression of virtual mass
force is employed:
2
vm
C V
F
v v
(4)
Consequently, th
vm f
p
p
f
e three interaction forces add up to the tot
interaction force considered in the CFD-D
method described in Zhao and S
to
al
EM coupling system
f
d
b
vm
F F F F
(5)
In computing the interaction forces, a divided void fraction
han (2012a, 2013) is followed
calculate and distribute the forces in the system more
accurately.
3 RESULTS AND DISCUSSION
3.1
Stokes Particle Settling Problem
The coupled CFD-DEM approach has first been benchmarked
by the classic problem of spherical particle settling in water
which was treated analytically by Stokes (1844). In the
numerical simulation, a sphere is released from the air to a
container half filled with water. Detailed model setup and
selection of model parameters of the numerical simulation can
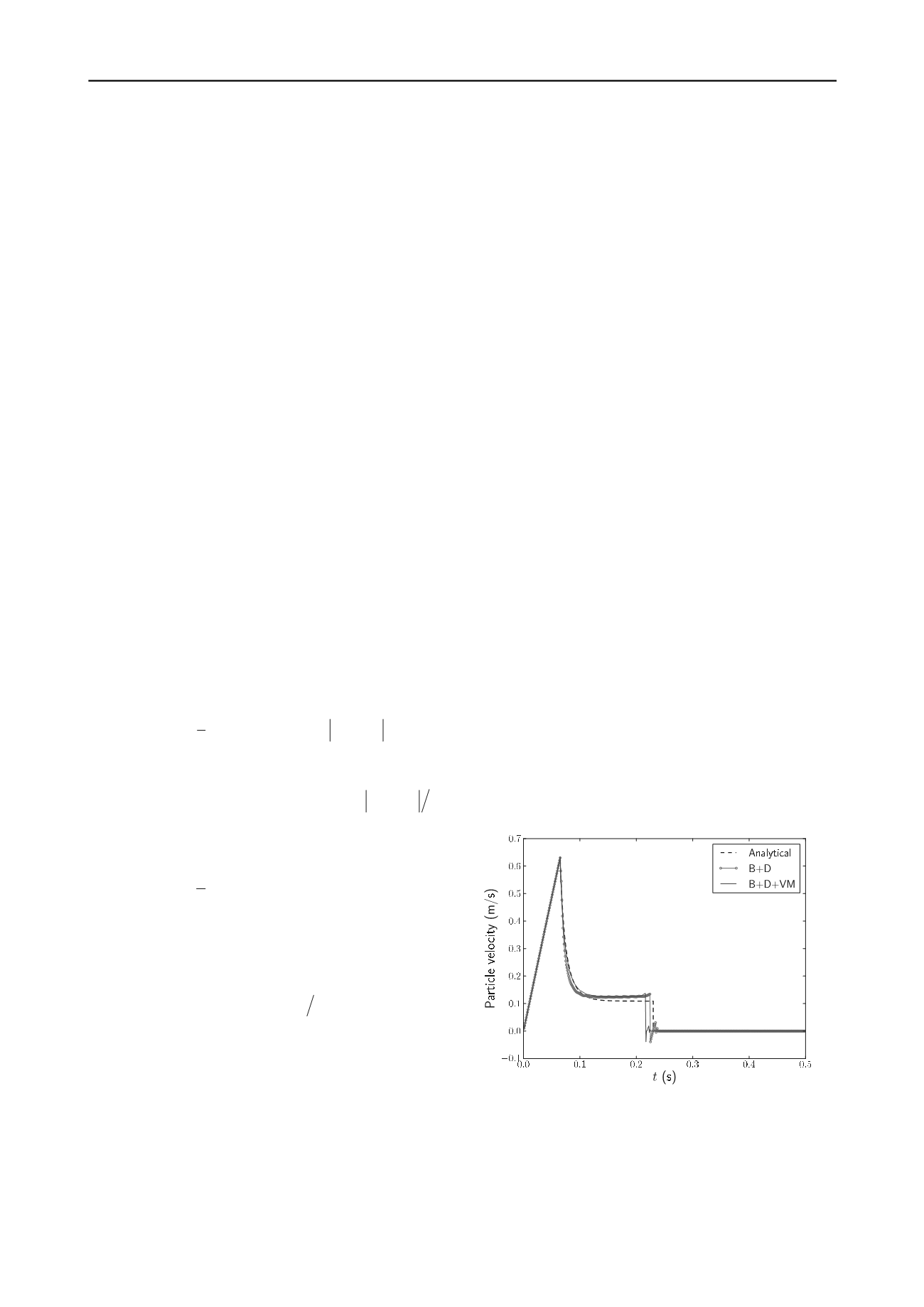
be found in Zhao and Shan (2012a). Presented in Fig. 1 is the
predicted settling velocity of the particle in comparison with the
analytical solution derived by Stokes (1844). In the figure, the
prediction denoted by “B+D” indicates the simulation only the
buoyancy force and drag force were considered (termed as
CASE I in the sequel), while the curve denoted with
“B+D+VM” was obtained by considering all three interaction
forces (hereafter this case will be called CASE II).
As can be seen, both cases of numerical simulations provide
reasonable predictions. The particle develops a peak velocity
before entering the water at
t
= 0.065 s. Upon entry into water,
it quickly decelerates to a steady terminal velocity at around
t
=
0.14 s before hitting the bottom of the container and bouncing
back. A good accordance is observed between the numerical
predictions with the analytical solution for both CASE I and
CASE II. There are nonetheless subtle differences between the
two cases. When the virtual mass force is considered in CASE
II, the deceleration process of the particle during the settling
between
t
= 0.065 s and
t
= 0.09 s is slightly quicker than in
CASE I when it is not considered, which also renders the
prediction in CASE II coincides more closely with the
analytical solution than CASE I during this stage of settling.
This may indicate that the consideration of virtual mass force
may reflect the effect of pushing away fluid in front of the
particle more reasonably. Meanwhile it is interesting to find the
particle in CASE II hits the bottom of the container and bounces
back slightly earlier than in CASE I. This is indeed not
surprising since the consideration of virtual mass force in CASE
II leads to changed velocity field in the fluid than in CASE I
which induces slightly smaller drag force during the settling
process. While the drag force is found the dominant one in all
interaction forces, the overall velocity of the particle in CASE II
is hence faster than in CASE I which render the particle to hit
the bottom earlier.
Figure 1. Comparison of the predicted particle settling velocity with the
Stokes’s analytical solution for a spherical particle settling from air to
water (B+D: in consideration of buoyancy force and drag force only;
B+D+VM: in consideration of all three interaction forces in Eq. (5)).


