3474
Proceedings of the 18
th
International Conference on Soil Mechanics and Geotechnical Engineering, Paris 2013
Duncan and Buchignani (1987) is not specified, but the
relationship was developed from in-situ testing and could
potentially represent a tangent or secant modulus at 50% of
peak strength. Thus, the strain levels for the estimated
E
u
and
E
in
may not be similar, and could explain the inaccuracy and
uncertainty shown in Figure 2.
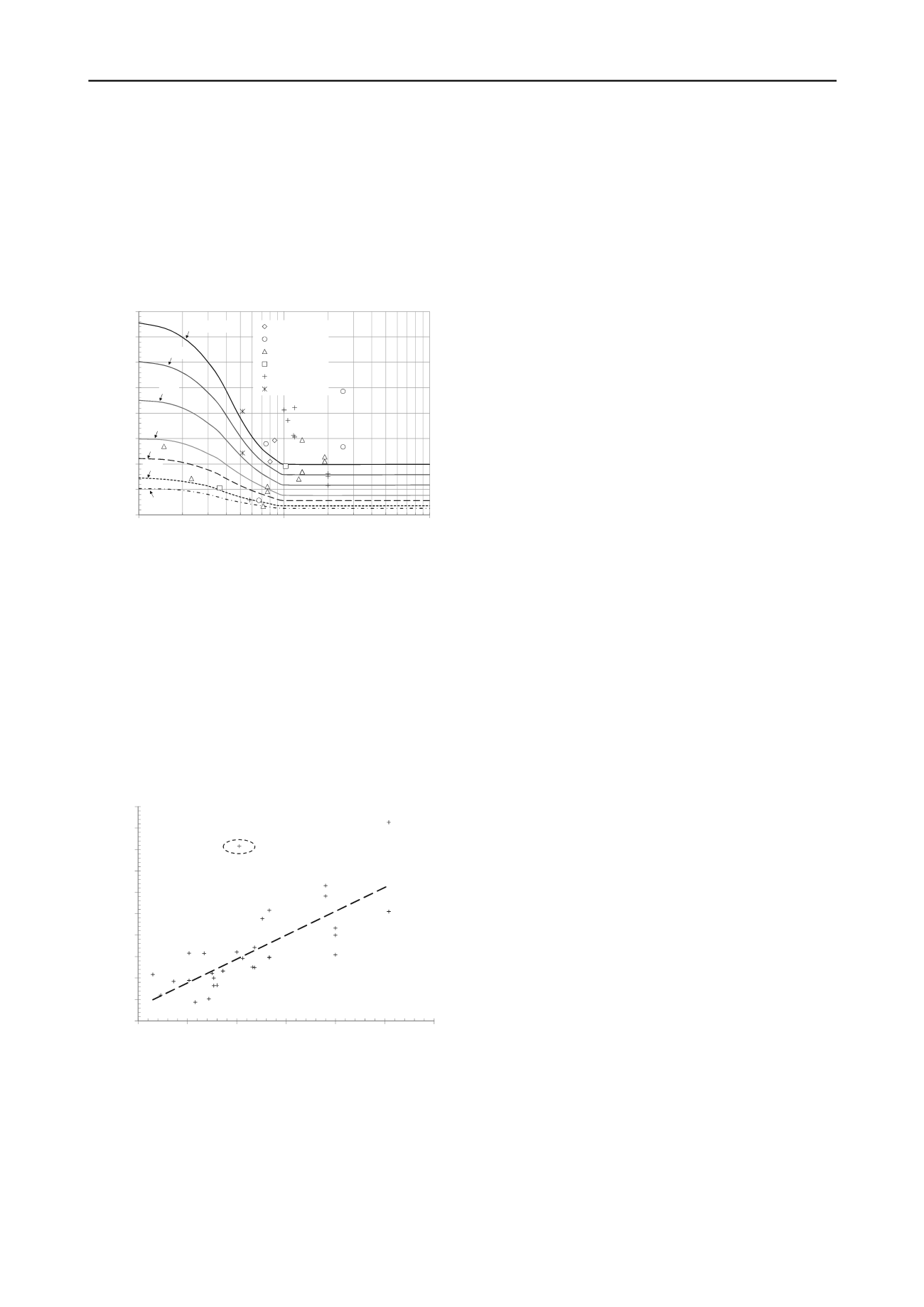
A new
K
was calculated using the back-calculated
E
in
and
the results are presented in Figure 2. The relationship proposed
by Duncan and Buchignani (1987) has been overlaid on the data
for comparison and appears to be independent of
PI
.
0
200
400
600
800
1000
1200
1400
1600
1
10
K
OCR
100
PI < 10
10 < PI < 20
20 < PI < 30
30 < PI < 40
40 < PI < 50
PI > 50
PI = 0
10
20
30
40
50
100
Figure 2. Back-calculated
K
-factor using non-linear model compared to
Duncan & Buchignani (1987).
6.2
Correlation to initial undrained Young’s modulus
When plotted against OCR, the back-calculated initial Young’s
modulus normalized by the atmospheric pressure,
p
atn
, exhibits
a linear trend line. The stiffness appears to increase with
OCR
.
A single footing used a 21 cm diameter tendon extended to
bedrock beneath the center of the footing in order to develop
displacements (Bauer 1976). The tendon likely interfered with
the failure mechanism of the soil beneath the footing and
produced a higher initial Young’s modulus. It was included in
the database because it was not considered a support mechanism
(drilled shaft, driven pile, etc.); however, it was omitted in
Figure 3 due to its clear departure from the trend.
E
in
/p
atm
= 11(OCR) + 33
R² = 0.64
0
50
100
150
200
250
300
350
400
450
500
0
5
10
15
20
25
30
E
in
/p
atm
OCR
Omitted
Figure 3. Back-calculated initial Young’s modulus using Duncan-Chang
model, based on Duncan & Buchignani (1987).
7 SUMMARY AND CONCLUSIONS
The use of a single undrained Young’s modulus to predict the
highly non-linear response of footings supported on cohesive
soil has been shown to be slightly conservative at low
displacements but increases in error with increasing
displacement. A method to estimate displacements based on the
non-linear Duncan-Chang model was shown to be slightly
conservative and more accurately captures the overall load-
displacement curve. The proposed method also allowed the
estimation of an initial undrained Young’s modulus, which
appears to be correlated with
OCR
. This trend can be used to
estimate the initial Young’s modulus for use in the non-linear
model or additionally modified to be used in elasticity based
methods.
Despite the improvement in modeling footing response
reported herein, signficant uncertainty in the response remains
without the adequate characterization of inherent soil
variability, transformation error associated with correlations,
and model error. Improved site characterization presents the
best approach to reducing the uncertainty of footing load-
displacement response.
8 REFERENCES
Bauer, G. E., Shields, D. H. and Scott, J. D., 1976. Predicted and
Observed Footing Settlements in a Fissured Clay. Ottawa, Pentech
Press, pp. 287-302.
Brown, P., 1969. Numerical Analyses of Uniformly Loaded Circular
Rafts on Deep Elastic Foundations. Geotechnique, 19(3), pp. 399-
404.
Burland, J., 1970. Discussion, Session A. London, British Geotechnical
Society, pp. 61-62.
Carrier, D.I. and Christian, J., 1978. Janbu, Bjerrum and Kjaernsli's
chart reinterpreted. Canadian Geotechnical Journal, Volume 15, pp.
123-128.
Das, B., 2011. Principles of Foundation Engineering. Seventh ed.
Stanford, CT: Global Engineering.
Davis, E. and Poulos, H., 1972. Rate of Settlement under two- and
three- dimensional conditions. Geotechnique, 22(1), pp. 95-114.
Duncan, J.M. and Buchignani, A., 1987. An Engineering Manual for
Settlement Studies, Berkeley: University of California.
Duncan, J.M. and Chang, C., 1970. Nonlinear Analysis of Stress and
Strain in Soils. Journal of the Soil Mechanics and Foundations
Division, 96(SM3), pp. 1629-1653.
Duncan, J.M., Byrne, P., Wong, K. and Mabry, P., 1980. Strength,
Stress-Strain and Bulk Modulus Parameters for Finite Element
Analyses of Stresses and Movements in Soil Masses, Berkeley:
University of California.
Elhakim, A. and Mayne, P.W., 2006. Foundation Load-Displacement
Response from Small-Strain Stiffness. Atlanta, ASCE, pp. 1-6.
Foye, K., Basu, P. and Prezzi, M., 2008. Immediate Settlement of
Shallow Foundations Bearing on Clay. International Journal of
Geomechanics, 8(5), pp. 300-310.
Holtz, R.D., 1991. Stress Distribution and Settlement of Shallow
Foundations. In: H. Fang, ed. Foundation Engineering Handbook.
2nd ed. New York: Chapman and Hall Inc., pp. 167-222.
Kondner, R., 1963. Hyperbolic Stress-Strain Response: Cohesive Soils.
Journal of the Soil Mechanics and Foundations Division, February,
89 (SM1), pp. 115-144.
Kulhawy, F.H. and Mayne, P.W., 1990. Manual on Estimating Soil
Properties for Foundation Design, Palo Alto: Electric Power
Research Institute.
Mayne, P.W. and Poulos, H., 1999. Approximate Displacement
Influence Factors for Elastic Shallow Foundations. Journal of
Geotechnical and Geoenvironmental, 125(6), pp. 453-460.
Osman, A. and Bolton, M., 2004. A New Approach to the Estimation of
Undrained Settlement of Shallow Foundations on Soft Clay.
Engineering Practice and Performance of Soft Deposits, pp. 93-98.
Perloff, W. and Baron, W., 1976. Soil Mechanics: Principals and
Applications. First ed. New York: Ronald Press Company.
Stuedlein, A. W. and Holtz, R. D., 2010. Undrained Displacement
Behavior of Spread Footings in Clay, pp. 653-669.
Strahler, A. W., 2012. Bearing Capacity and Immediate Settlement of
Shallow Foundations on Clay.
Vesic, A., 1973. Analysis of Ultimate Loads of Shallow Foundations.
Journal of the Soil Mechanics and Foundations Division, 99(1), pp.
45-73.


