3472
Proceedings of the 18
th
International Conference on Soil Mechanics and Geotechnical Engineering, Paris 2013
Regression analyses on Burland’s charts yielded a simple
representation of
I
E
(Strahler 2012):
f
eq
E
D
B
e
I
s
4.0 22.1
5.3
1
1
(2)
In addition to embedment effects, stresses below a spread
footing are also affected by the rigidity of the foundation. The
rigidity correction factor,
I
F
, is used to modify the stress
distribution to account for foundation rigidity and is given by
(Mayne and Poulos 1999):
f
F
K
I
10 6.4
1
4
(3)
where
K
f
= the foundation flexibility factor (Brown, 1969) and
is a function of the modulus of the soil as well as the modulus,
thickness and radius of the foundation.
Soil profiles that exhibit a linear increase in modulus with
depth, termed a Gibson profile (e.g., Mayne & Poulos, 1999),
may be modeled using the Gibson displacement influence
factor,
I
G
, given by:
8.0
75.0 27.1
1
eq E
o
G
Bk
E
I
(4)
where
E
o
is Young’s modulus of the soil directly beneath
foundation,
k
E
is the rate of increase of modulus with depth.
The use of Eqn. (1) requires an estimate of soil stiffness; for
undrained loading of footings on clay the appropriate stiffness
for linear elastic models is the undrained Young’s modulus,
E
u
.
Although many correlations to
E
u
exist (e.g., Kulhawy and
Mayne 1990), Duncan and Buchignani (1987) suggested that
E
u
was linearly proportional to undrained shear strength,
s
u
, and
proposed the following commonly used expression:
u
u
Ks E
(5)
where
K
= the constant of proportionality and is a function of
stress history and soil plasticity. Duncan and Buchignani (1987)
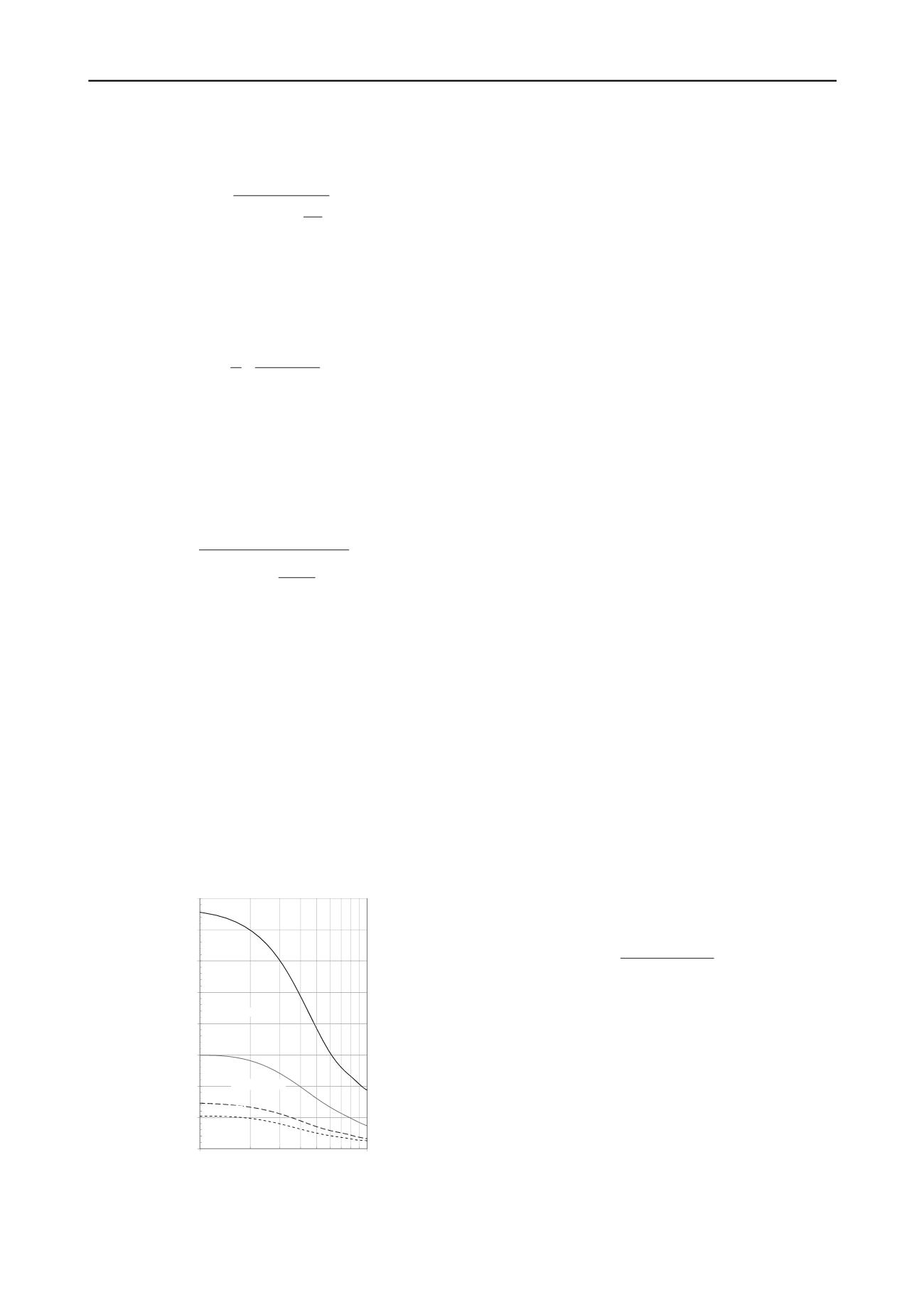
proposed Figure 1 to indicate the sensitivity of
K
to plasticity
index (
PI
) and overconsolidation ratio (
OCR
).
0
200
400
600
800
1000
1200
1400
1600
1
K
OCR
10
PI < 30
30 < PI < 50
PI > 50
Figure 1. Variation in the
K
-factor based on
OCR
and
PI
(adapted from
Duncan and Buchignani 1987).
2.2
Non-linear distortion displacement models
Several researchers have pointed to the limitations of linear
elastic-perfectly plastic model behavior and developed non-
linear distortion displacement models that attempt to more
accurately estimate displacements (Osman and Bolton, 2004;
Elhakim and Mayne, 2006; Foye, et al., 2008). These methods
are either computationally intensive, require significant or
potentially expensive subsurface information, or rely on FEAs
that assume homogeneous or isotropic soil conditions and are
limited to specific stress conditions. As a result they may not be
applicable to many realistic design scenarios and are limited in
their appropriate uses.
3 LOAD TEST DATABASE AND STATISTICAL
APPROACH FOR IMMEDIATE SETTLEMENT MODEL
EVALUATION
3.1
Development of load test database
To evaluate the uncertainty in the linear elastic distortion
settlement calculation and provide the basis for a new model, a
database of case histories was developed. The database was
initially populated with 24 case histories and was subsequently
reduced to 12 with 30 individual footing load tests based on the
quality of soil and load test information. The stress histories
represented in the database largely consist of lightly to heavily
overconsolidated soil profiles, with just one true normally
consolidated soil profile. The database included 13 square
foundations and 17 circular footings. Twenty-eight of the
footings were embedded below the ground surface. Further
details on the load test database are given in Strahler (2012),
and are not described here for brevity.
3.2
Statistical approach
The accuracy of the immediate settlement models evaluated
herein was characterized using the mean bias,
, defined as the
ratio of an observed and calculated displacement, and its
distribution. Distributions of the sample bias values were
assessed using goodness of fit metrics, and appropriate second
moment statistics were determined. The coefficient of variation
(
COV
) of the bias, defined as the standard deviation in bias
divided by its mean, is used herein as a convenient
representation of dispersion. Details regarding distribution
fitting are given by Strahler (2012).
4 EVALUATION OF THE ELASTICITY-BASED
APPROACH
Equation (1) was rearranged to compute the elasticity-based
bearing pressure,
q
e
app
, for each displacement,
δ
i
, for a given
load-displacement curve:
2
1
s
EFG eq
i u
e
app
IIIB
E
q
(6)
To evaluate the performance of Eqn (6) using the footing
load test database, the undrained shear strength was averaged
over
B
eq
and the constant of proportionality,
K,
was linearly
interpolated from Figure 1 for data pairs of
PI
and
OCR
. The
upper dark line was assumed to correspond to a
PI
= 0, whereas
the lower dashed line was assumed to correspond to a
PI
= 100.
For case histories with soil layers characterized with
OCR
s
greater than 10,
K
was assumed to be equal to the value at
OCR
= 10 (Figure 1).
Following the computation of bearing pressures, the sample
biases were calculated and their statistical distribution
determined. The mean bias for a displacement of 10 mm was
0.85, indicating that the undrained Young’s modulus estimated
using Figure 1 and Eqn. (6) is moderately un-conservative (i.e.
the calculated bearing pressure for 10 mm of displacement is


