1040
Proceedings of the 18
th
International Conference on Soil Mechanics and Geotechnical Engineering, Paris 2013
conditions pose a severe problem for simulating flow through
porous media because the intrinsic permeability becomes
viscosity dependent, while it should be a characteristic of the
physical properties of porous medium alone. The deficiencies
inherent in the BGK model can be significantly reduced by
using a multiple-relaxation-time (MRT) approach (He et al.
1997), which separates the relaxation times for different kinetic
modes and allows tuning to improved numerical stability and
accuracy. In this study we used D2Q9 MRT as they were
introduced by Lallemand and Lue (2000), Extensive details can
be found in Lallemand and Lue (2000), and
Li et al. (2005).
The Lattice-Boltzmann method for single-phase flow
describes fluid flow as collisions of mass particles in a lattice
(Chen et al., 1992). In two-phase flow, we follow almost the
same procedures as in the single-phase case, except that we
have two different types of particles representing two
immiscible fluids, and we need to calculate surface tension and
wettability. There are several popular Lattice Boltzmann (LB)
techniques for the analysis of multiphase flows, three of which
are the methods of Gunstensen et al. (1991), Shan & Chen
(1993), and free energy approach by Swift et al. (1996). All
three methods have been employed in numerical researches and
each one has its distinct advantages. A review of these methods
can be found in Nourgaliev et al. (2003). Among all of these
LBM models, Shan & Chen’s model (SC model) is widely used
due to its simplicity and remarkable versatility. It can handle
fluid phases with different densities, viscosities and
wettabilities, and handle different equations of state as well. In
this study, the multi-component (2 fluids) single phase version
of SC model has been applied (Sukop &Thorne, 2006).
3 VERIFICATION
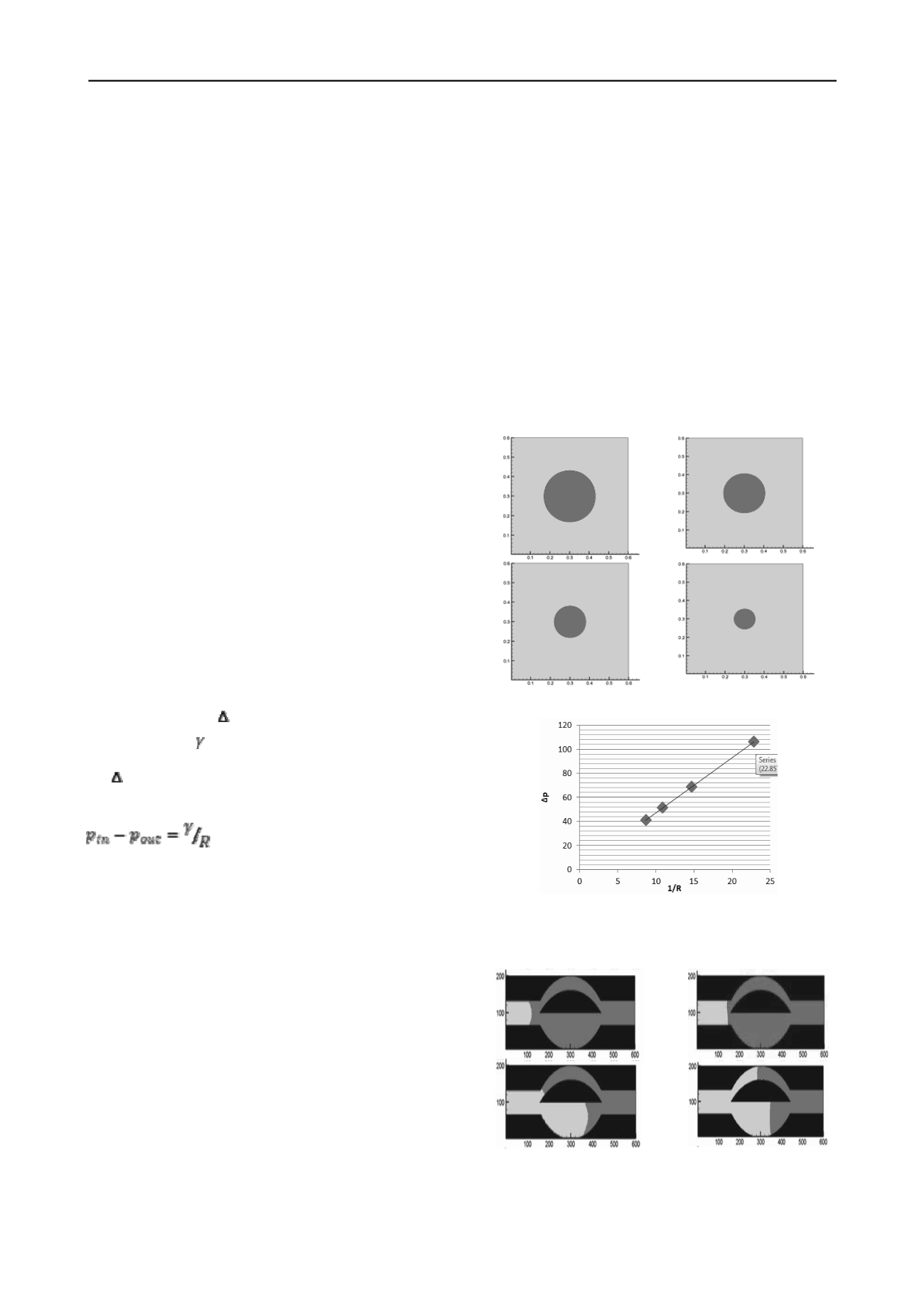
In multi-component LB models, the bubble test is often
conducted to check the ability of the model in relating the
pressure difference (
p
), radius of curvature (
R
) and
interfacial tension ( ) together in the situation that a bubble of
one fluid is immersed in another fluid, which should indicate
that
p
varies linearly with respect to curvature 1/
R
based on
the well-known Laplace law:
(1)
Four different sizes of bubbles (Figure 1) are used for the
numerical experiments. Figure 1b shows the capillary pressures
for four different bubbles. The theoretical prediction is shown as
a solid line. The simulated values (symbols) are obtained by
simply calculating pressures inside and outside the bubbles at
the end of the numerical simulations. The numerical results
show very good agreement with the theoretical values.
Another well-studied model of immiscible displacement, the
so-called pore doublet model, is a little more complicated. A
typical pore doublet consists of two tubes with different
diameters, joined at both ends (Figure 2). Since the capillary
pressure is inversely proportional to the radius of the tube, the
capillary pressure of the smaller tube is greater than that of the
bigger tube. Drainage-type snap-off occurs when the external
pressure gradient is big enough to overwhelm the capillary
pressure of the bigger tube, but is not big enough for the smaller
tube. Theory and laboratory experiments show that under this
condition the wetting phase in the smaller tube is trapped, while
that in the bigger tube it is replaced by the non-wetting phase
(Lenormand et al., 1983). Figure 2show that the two-phase
Lattice-Boltzmann method successfully replicates the drainage-
type snap-off, which tells us that the method accurately
describes capillary pressure phenomena of porous media. If the
displacing fluid is wetting, then both tubes will be swept out by
the wetting fluid (figure 2.b)
4 RELATIVE PERMEABILITIES
One of the most comprehensive sets of experimental works
regarding relative permeability was pursued by Payatakes and
his co-workers (Valavanides et al. 1998, Tsakiroglou et al.
2007) who performed experiments on the steady and unsteady
flow regimes in porous core consisting of a chamber-and-throat
network. Here, both steady and unsteady states experiments of
Payatakes were selected for evaluation of the results of the
developed LBM model. The dimensions of their specimen is
0.16 ×0.11 m, and its absolute permeability is k = 8.9 μm
2
. The
distance between the centers of the adjacent chambers is 1221
μm, the mean throat depth is 116.6 μm, and the mean throat
width is 167.5 μm.
a
b
Figure 1. (a) Four different sizes of bubbles in steady-state condition (b)
capillary pressure vs. reciprocal of bubble radius. Simulated values
(symbols) agree well with the theoretical prediction (solid line).


