1597
Technical Committee 203 /
Comité technique 203
nduisant à l'équilibre de la paroi. Exemple
d'un sol purement frottant.
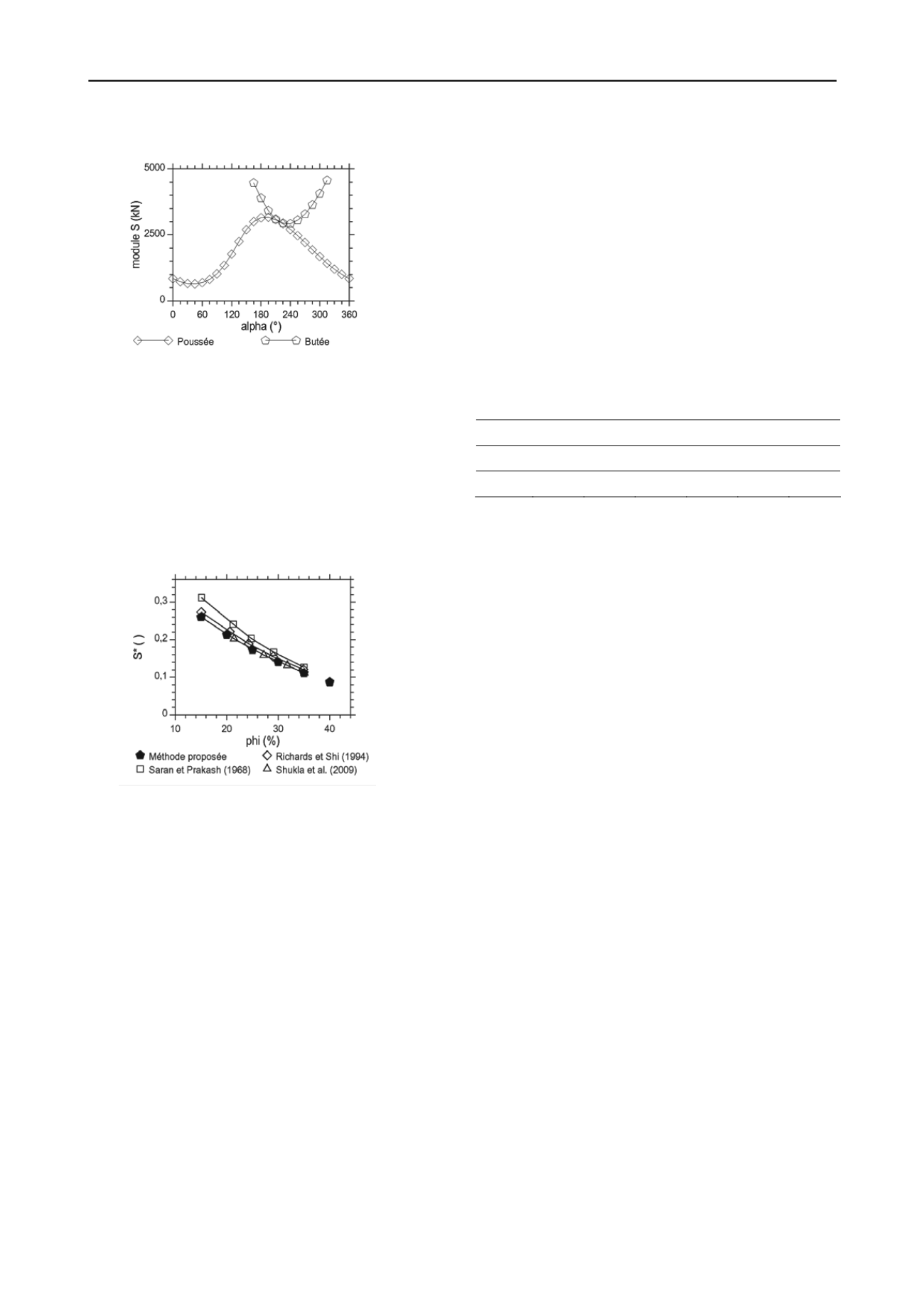
e et le minimum
de butée comme le montre le graphique (
, S).
.3 Comparaison avec d'autres méthodes
Figure 5.
ifférents
auteurs et par la méthode proposée (pentagones).
poussées d'un sol cohérent par
un
, mais ils décroissent
av
des forces de poussées sur la paroi proposée par Shukla et al.
Figure 4. Efforts de poussée et de butée en fonction de l'angle
pour
une résistance du terrain co
L'exemple d'un sol purement frottant est donné sur la
figure 4. Le calcul est effectué en trois itérations sur l'angle de
frottement pour aboutir à
= 29,5 ° et obtenir l'équilibre.
L'angle
vaut
= 210 ° environ. Mais les modules S des forces
en présence ne sont pas le maximum de poussé
3
Comparaison des efforts de poussée calculés par d
L'estimation des poussées sur un soutènement pendant un
séisme est un problème ancien en géotechnique. La solution
souvent utilisée, dite Mononobe – Okabe, s'applique au cas d'un
sol non cohérent (Okabe, 1926 : Mononobe, 1929 ; Seed et
Whitman, 1970 ; Das, 1998 ; Shukla et al., 2009). Elle est
dérivée directement du calcul de l'équilibre d'un coin de
Coulomb dans lequel ont été introduits des efforts inertiels
quasi-statiques horizontaux et verticaux. Cette solution a été
étendue au cas d'un sol cohérent et frottant (c -
) par Saran et
Prakash (1968) en considérant seulement la composante
horizontale de l'accélération sismique, puis au cas d'un massif
incliné (Saran et Gupta, 2003). Richard et Shi (1994) avaient
proposé une autre expression des
e approche en élastoplasticité.
Shukla et al. (2009) proposent une expression de la force de
poussée basée sur l'équilibre d'un coin de Coulomb soumis à
une accélération verticale et une accélération horizontale. Ces
accélérations sont définies par les coefficients multiplicateurs k
v
et k
h
de l'accélération g. Les calculs paramétriques des auteurs
montrent que la pente du plan de rupture décroît avec
l'accroissement des coefficients k et que la décroissance est plus
rapide pour les fortes valeurs de ces coefficients. Les efforts de
poussée augmentent avec le coefficient k
h
ec k
v
, sauf pour les fortes valeurs de k
h
.
La figure 5 montre une comparaison des méthodes de calcul
(2009). La cohésion du sol c et la force de poussée S sont
indiquées sous une forme adimensionelle c
*
et S
*
:
c
*
= c /
h
S
*
= S /
h
2
(5)
où h est la hauteur de l'écran et
le poids volumique du sol.
L'expression de Shukla et al. (2009) pour le calcul des poussées
sur l'écran résulte de l'équilibre des forces appliquées au coin.
Les hypothèses adoptées dans cette étude sont identiques à
celles des auteurs. Les résultats obtenus concordent.
La méthode développée dans les paragraphes précédents a
été mise en œuvre pour calculer les réponses S
*
en fonction de
dans le cas particulier suivant, qui se rapporte à la figure 5 :
k
v
= 0, k
h
= 0,10 soit
= 180 °, a
v
= 9,81 m/s
2
, a
h
= 0,981 m/s
2
,
= 18 kN/m
3
,
=0 °, h =10 m, c
*
= 0,05, c =
h c
*
= 9 kPa.
Tableau 1. Exemples de caractéristiques de résistances non drainées des
ols. s
(°)
15
20
25
30
35
40
S(kN)
18,7
15,3
12,5
10,1
8,0
6,2
S
*
( )
0,26
0,21
0,17
0,14
0,11
0,09
Les forces de poussée S et leurs valeurs adimensionnelles S
*
sont indiquées dans le tableau 1. Les couples (
, S
*
) sont
reportés sur le graphique de la figure 5 (figurés pleins). Ces
résultats coïncident avec ceux de Shukla et al. (2009).
4 PRESENCE DE PRESSIONS D'EAU
4.1 Expressions simplifiées
Des pressions d'eau sont introduites dans le massif et sur toute
sa hauteur. Elles s'appliquent perpendiculairement aux segments
AB et AC du coin, dans les directions
n
et
i
respectivement.
Leur répartition est triangulaire. Leurs résultantes sont notées
K
et
H
respectivement, qui s'appliquent aux points K et H comme
indiqué sur la figure 2.
Ces pressions interstitielles et les efforts associés peuvent
être définis à partir de la contrainte verticale totale
vA
qui règne
au point A dans un champ géostatique
vA
=
h et un
coefficient r
u
à définir. La pression interstitielle en A s'écrit
ainsi u
A
= r
u
vA
= r
u
h. Les modules H et K sont alors, à
comparer au poids W =
h
2
/ 2 tg
:
H = r
u
h u
A
/ 2 = r
u
h
2
/ 2
K = r
u
h u
A
/ 2 sin
= r
u
h
2
/ 2 sin
(6)
Pour un calcul en contraintes effectives et en présence de
pressions d'eau, le coefficient r
u
est non nul (r
u
0) et la force
K
vient en déduction de la force normale
N
. La force effective
appliquée à l'écran est
S
–
H
. Pour un calcul en contraintes
totales, le coefficient r
u
est nul (r
u
= 0) et les forces
K
et
H
sont
nulles (
K
=
0
,
H
=
0
). Les équations d'équilibre deviennent :
P
+
S
+
N
+
T
+
H
+
K
+
F
=
0
(7)
M
PA
+ M
SA
+ M
NA
+ M
HA
+ M
KA
+ M
FA
= 0
En introduisant les vecteurs unitaires des directions des
efforts, les signes s = 1 en poussée et s = -1 en butée (pour
indiquer la direction
t
), l
AD
= r l
AC
la distance AD d'application
de
S
sur l'écran, fraction de la longueur AC (r coefficient
pouvant être différent de 1/2 ici), l
AE
= d la distance AE et
(x
p
, y
p
) et (x
f
, y
f
) les coordonnées des vecteurs unitaires
p
de
P
et
f
de
F
, puis les coordonnées des vecteurs
s
de
S
,
n
de
N
,
t
de
T
,
h
de
H
et
k
de
K
, les trois premières équations se résolvent
en N et S par le système suivant qui est dérivé du précédent :
x
s
S + (x
n
+ x
t
tg
) N =
x
t
(tg
K – C) – x
p
P – x
h
H – x
k
K – x
f
F


